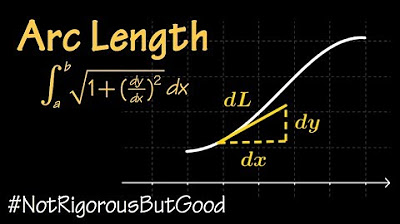Arc Length Calculus Problems,

The Organic Chemistry Tutor

4 Mar 201730:47

EducationalLearning

32 Likes 10 Comments

TLDRThe video script is a comprehensive guide on calculating the arc length of a curve. It introduces the formula for arc length, which involves integrating the square root of one plus the derivative squared from one point to another on the curve. The script then walks through several examples, each with different functions and intervals, demonstrating how to find the derivative, apply the arc length formula, and use substitution methods when necessary. The examples include a variety of functions, such as power functions and those involving both x and y variables. The script provides detailed steps and calculations, leading to the final arc lengths in both exact and approximate values.

Takeaways

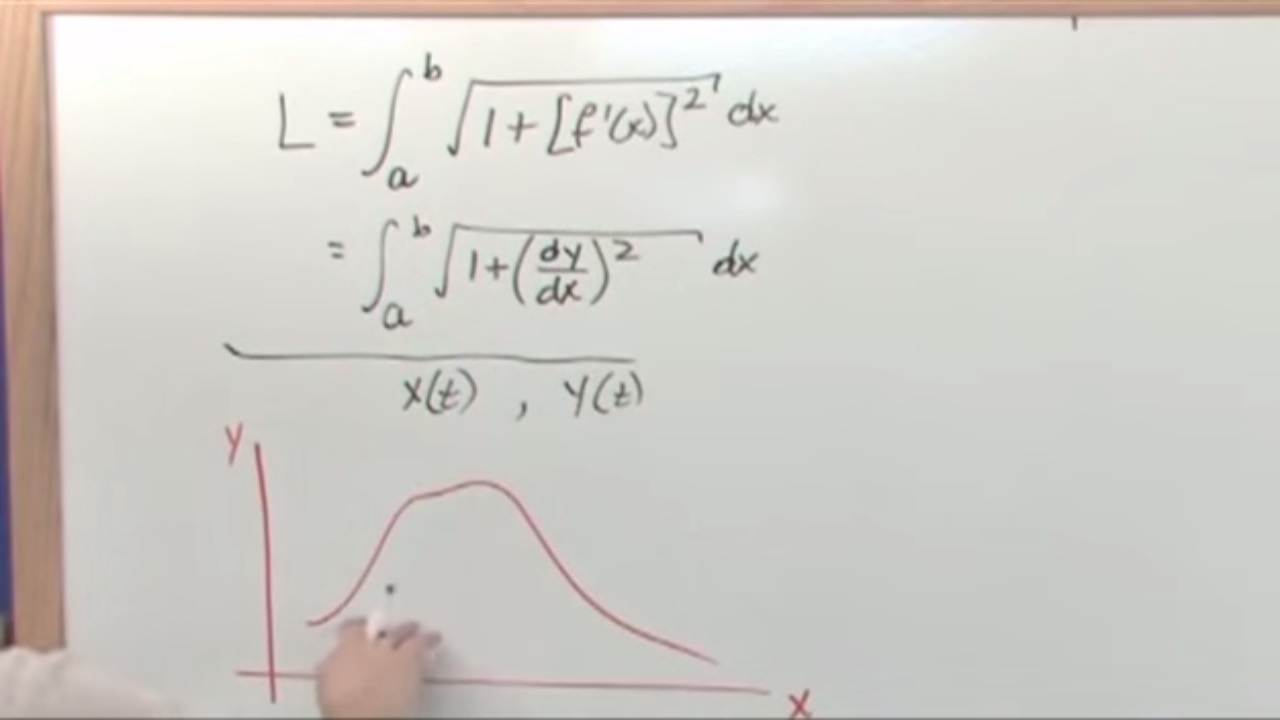
📚 The formula for calculating the arc length of a curve is given by the integral from point A to point B of the square root of (1 + (f'(x))^2) dx, where f'(x) is the derivative of the function f(x).
🌟 In some texts, the arc length formula may use 's' instead of 'l' and 'dy/dx' instead of 'f''(x), but they all represent the same concept.
🧠 To find the arc length, first determine the function's derivative and then square it to use in the arc length formula.
📝 Example 1: For f(x) = 1 + 6x^(3/2), the arc length from (0,0) to (1,f(1)) is calculated using the integral of (1 + (9x^(1/2))^2) dx from x=0 to x=1.
🔄 In the first example, a u-substitution is performed with u = 1 + 81x, and the limits of integration are adjusted accordingly to find the arc length.
📊 Example 2: For y = (3/2)x^(2/3), the arc length from x=1 to x=8 is found by integrating the square root of (1 + (x^(-1/3))^2) dx from x=1 to x=8.
🧩 In the second example, the expression is modified and factored to allow for u-substitution, resulting in a simpler integral to solve.
📝 Example 3: When the function is given in terms of y (x = f(y)), the arc length is found using the integral from the lower to the upper limit of the y-values, with the formula 𝑙 = ∫√(1 + (dx/dy)^2) dy.
🔢 For the third example, the derivative dx/dy is calculated from the given x = f(y), and then squared for use in the arc length formula.
📈 The arc length formula can be applied to various types of functions and requires the use of integration and differentiation techniques to find the solution.
🎓 Understanding the arc length formula and its application is crucial for solving problems involving the length of curves in calculus.

Q & A

What is the general formula for calculating the arc length of a curve?
-The general formula for calculating the arc length of a curve is given by the integral from point A to point B of the square root of (1 + (f'(x))^2) dx, where f'(x) represents the derivative of the function f(x) with respect to x.
How do you find the derivative if the function is given in terms of x?
-To find the derivative of a function given in terms of x, you apply the usual differentiation rules, such as the power rule, chain rule, etc., to find f'(x) which is the derivative of the function f(x) with respect to x.
What is the alternative notation for the arc length formula?
-An alternative notation for the arc length formula is to replace f'(x) with (dy/dx), which essentially means the same thing, and also to use s instead of l, but the formula structure remains the same.
How do you apply u-substitution in arc length problems?
-In arc length problems, u-substitution is applied by letting u equal to the expression inside the square root in the integrand. Then, you find the derivative of u with respect to x (du/dx), and replace dx with du/(dx/du) in the integral. The limits of integration are also adjusted according to the new variable u.
What was the first example problem in the transcript, and how was it solved?
-The first example problem involved finding the arc length of the curve defined by f(x) = 1 + 6x^(3/2) from x=0 to x=1. The solution involved finding the derivative f'(x) = 9x^(1/2), squaring it, and then applying the arc length formula and u-substitution to evaluate the integral.
How do you handle a function that is given in terms of y for arc length calculations?
-When a function is given in terms of y, you first find the derivative dx/dy using the chain rule. Then, you square this derivative and use the arc length formula with integration from c to d of the square root of (1 + (dx/dy)^2) dy, where c and d are the y-coordinates of the interval.
What is the significance of the perfect square trinomial in arc length problems?
-The perfect square trinomial is significant in arc length problems because it allows for simplification of the integrand. It can be factored into a square of a binomial, which simplifies the square root in the arc length formula and often makes the integration process easier.
What was the second example problem in the transcript, and how was it solved?
-The second example problem involved finding the arc length of the curve defined by y = (3/2)x^(2/3) from x=1 to x=8. The solution involved finding the derivative dx/dy, squaring it, and then applying the arc length formula with u-substitution to evaluate the integral.
How do you evaluate a definite integral in arc length problems?
-To evaluate a definite integral in arc length problems, you first find the antiderivative of the integrand, then you apply the limits of integration (the values of the variable at the start and end points of the curve) to the antiderivative to find the difference in its values at these limits.
What is the importance of factoring out the common factor in the integrand during arc length calculations?
-Factoring out the common factor in the integrand is important because it can simplify the integrand and make the integration process easier. It can also help in applying u-substitution or other techniques to solve the integral more efficiently.
What was the third example problem in the transcript, and how was it solved?
-The third example problem involved finding the arc length of the curve defined by x = (1/3)sqrt(y) + y^(2/3) from y=0 to y=4. The solution involved expressing x in terms of y, finding the derivative dx/dy, squaring it, and then applying the arc length formula to evaluate the integral.
What is the final example problem presented in the transcript, and what steps are involved in solving it?
-The final example problem involves finding the arc length of the curve defined by x = (1/3)sqrt(y) * y - 3 from y=1 to y=9. The steps involved include rewriting square root y as y^(1/2), finding the derivative dx/dy, squaring it, and then using the arc length formula with u-substitution and factoring to evaluate the integral.

Outlines

00:00

📚 Calculating Arc Length with Integration

This paragraph introduces the concept of calculating the arc length of a curve using integration. It presents the general formula for arc length, which involves integrating the square root of one plus the derivative of the function squared over the interval from point A to point B. The paragraph also explains alternative notations found in textbooks and provides an example of finding the arc length for the function f(x) = (1 + 6x^(3/2))^2 from 0 to 1. The explanation includes finding the first derivative, squaring it, and setting up the integral using u-substitution to simplify the calculation.

05:01

🔢 Solving Arc Length with Power Functions

The second paragraph continues the discussion on arc length by tackling another example involving a power function. It explains the process of finding the derivative of the function y = (3/2)x^(2/3) and using the arc length formula over the interval from 1 to 8. The paragraph demonstrates how to simplify the integrand by factoring out the common factor and integrating term by term. The final result is given in both radical and approximate decimal form.

10:01

📐 Arc Length with Function in Terms of Y

This paragraph addresses a scenario where the function is given in terms of y, rather than x. It introduces the formula for arc length in terms of y and demonstrates its application through an example where x = (1/3)y^2 + 2^(3/2) and y ranges from 0 to 4. The explanation involves finding the derivative with respect to y, squaring it, and setting up the integral. The integral is then evaluated, resulting in a final answer expressed as an improper fraction.

15:01

🌀 Integrating Complex Arc Length Formulas

The fourth paragraph delves into a more complex example of calculating arc length, where x is expressed as a function involving the square root of y and y - 3. The interval for y is from 1 to 9. The paragraph outlines the steps of rewriting the function, finding the derivative with respect to y, and squaring the derivative to set up the integral. It also explains how to simplify the integrand by factoring and using the arc length formula to find the final result.

20:02

📈 Evaluating Integrals for Arc Length

The fifth paragraph focuses on evaluating the integral for arc length in a specific example. It involves a function x = √y * y - 3 with y ranging from 1 to 9. The paragraph details the process of finding the derivative, squaring it, and setting up the integral expression. It then demonstrates how to simplify the integrand by factoring out common terms and applying the arc length formula. The final result is obtained by integrating and evaluating the expression at the given interval's limits.

25:05

🔍 Complex Integration for Arc Length

The sixth paragraph presents a challenging example of calculating arc length through integration. The function x is given as 1/3√y * y - 3 with the interval for y from 1 to 9. The paragraph explains the steps of finding the derivative, squaring it, and setting up the integral. It then shows how to simplify the integrand by factoring and using the arc length formula. The final result is calculated by evaluating the integral at the specified limits and presented as a fraction.

30:06

📊 Final Arc Length Calculation

The final paragraph concludes the discussion on arc length with a complex example. The function x is defined as 1/3√y * y - 3 for y ranging from 1 to 9. The paragraph outlines the process of finding the derivative, squaring it, and setting up the integral. It demonstrates how to simplify the integrand by factoring and applying the arc length formula. The final result is obtained by evaluating the integral at the given interval's limits and presented as a simplified fraction.

Mindmap

Keywords

💡Arc Length

Arc length refers to the distance along the curve of a function from one point to another. In the context of the video, it is calculated using integral calculus, where the formula involves integrating the square root of one plus the derivative of the function squared from one limit to another. This concept is central to the video's theme of exploring mathematical concepts related to curves and their properties.

💡Integration

Integration is a fundamental concept in calculus that involves finding the area under a curve or, in the case of arc length, the antiderivative of a given function. It is used to compute the arc length by integrating a specific expression derived from the function that describes the curve. In the video, integration is the primary method used to solve for arc lengths in various scenarios.

💡Derivative

A derivative represents the rate of change of a function with respect to its variable, often denoted as f'(x) or dy/dx. In the context of the video, derivatives are crucial for finding the arc length, as they are squared and integrated to determine the distance along the curve. The first derivative is particularly important as it is used directly in the arc length formula.

💡Power Rule

The power rule is a basic differentiation rule in calculus that states if f(x) = x^n, then f'(x) = n*x^(n-1). This rule is used to find the derivative of functions involving exponents. In the video, the power rule is applied to various functions to compute their derivatives, which are then used in arc length calculations.

💡U-Substitution

U-substitution, also known as variable substitution, is a technique used in calculus to simplify integrals by replacing a part of the integrand with a new variable, u. This makes the integration process easier, especially when dealing with complex expressions. In the video, u-substitution is used to transform the integral for arc length into a more manageable form.

💡Chain Rule

The chain rule is a differentiation technique used when dealing with composite functions, which involves differentiating the outer function and then multiplying by the derivative of the inner function. It is essential for finding derivatives of complex functions and is used in the video to compute the derivative of functions expressed in terms of another variable, such as x in terms of y.

💡Perfect Square Trinomial

A perfect square trinomial is a quadratic expression that can be factored into the square of a binomial. It has the form a^2 + 2ab + b^2, where a and b are constants. In the context of the video, recognizing and factoring perfect square trinomials simplifies the integration process for calculating arc lengths.

💡Factoring

Factoring is the process of breaking down a polynomial into its constituent factors, which simplifies the expression and makes further calculations, such as integration, easier. In the video, factoring is used to simplify complex integrands before integrating to find arc lengths.

💡Antiderivative

An antiderivative, also known as an indefinite integral, is a function that represents the reverse process of differentiation. It is used to find the original function whose derivative is a given function. In the context of the video, antiderivatives are sought to evaluate integrals and find arc lengths.

💡Limits of Integration

The limits of integration, also known as the bounds of integration, define the interval over which an integral is evaluated. These limits are crucial in determining the specific portion of the curve under consideration. In the video, the limits of integration are adjusted based on the function and the problem at hand to calculate the correct arc lengths.

💡Square Root

A square root is a mathematical operation that finds a number which, when multiplied by itself, gives the original number. In the context of the video, square roots are used in the formulas for calculating arc lengths and in simplifying integrands before integration.

Highlights

The concept of finding the arc length of a curve is introduced, which is a fundamental topic in calculus.

The arc length formula is presented, which is essential for calculating the length of a curve between two points.

An example is provided to demonstrate how to apply the arc length formula to a specific function.

The process of finding the first derivative of a function is explained, which is a crucial step in applying the arc length formula.

The use of the power rule in differentiation is highlighted, which is a key technique in calculus.

The concept of u-substitution is introduced as a method to simplify integrals in the arc length formula.

The importance of changing the limits of integration when using u-substitution is emphasized.

The process of integrating a function involving a square root and a power is demonstrated.

The method of factoring out a common factor is shown to simplify the integration process.

The concept of perfect square trinomials is utilized in the integration process.

The process of evaluating the integral at the new limits is explained.

The calculation of the arc length for a function defined in terms of y is presented.

The chain rule is applied to find the derivative of a composite function.

The method of separating a complex radical into two simpler radicals is demonstrated.

The process of evaluating the integral and simplifying the result is shown.

The concept of converting the final answer into a decimal equivalent for practical applications is mentioned.

The final example involves finding the arc length relative to the y-axis, showcasing a different approach.

The method of foiling is introduced to simplify the integration of a quadratic expression.

The process of combining like terms and simplifying the expression before integrating is highlighted.

The final answer is provided in a simplified form, demonstrating the culmination of the integration process.

Transcripts

Browse More Related Video

Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

Arc Length of y=x^(3/2) | MIT 18.01SC Single Variable Calculus, Fall 2010

Finding Arc Length Using an Integral

Arc Length (formula explained)

AP Calculus BC Lesson 8.13

Arc Length (Calculus 3)

Related Tags

Mathematics Calculus Arc Length Integrals Derivatives Education Tutorial Math Examples Geometry Functions