Evaluating Definite Integrals Using Geometry
TLDRThe video script is an educational guide on evaluating definite integrals using geometric methods. It explains how to calculate the area under a function over a given interval by visualizing and breaking down the shape into fundamental geometric figures like rectangles and triangles. The script provides several examples, including integrating a horizontal line, a straight line with a slope, and a function involving absolute values. It also covers the unique case of integrating a semicircle, highlighting the importance of recognizing the shape represented by the function to apply the correct geometric principles for the calculation.
Takeaways
- 📈 The value of a definite integral can be found by evaluating the area under a curve within a given interval.
- 📊 To find the area of a shape, one must first graph the function and then determine the dimensions of the shape (rectangle, triangle, etc.).
- 🤔 For a horizontal line, the area under the curve is simply the width of the interval multiplied by the constant value of the function.
- 📐 When dealing with a linear function like 2x, the area of the shaded region is a right triangle, calculated as 1/2 base times height.
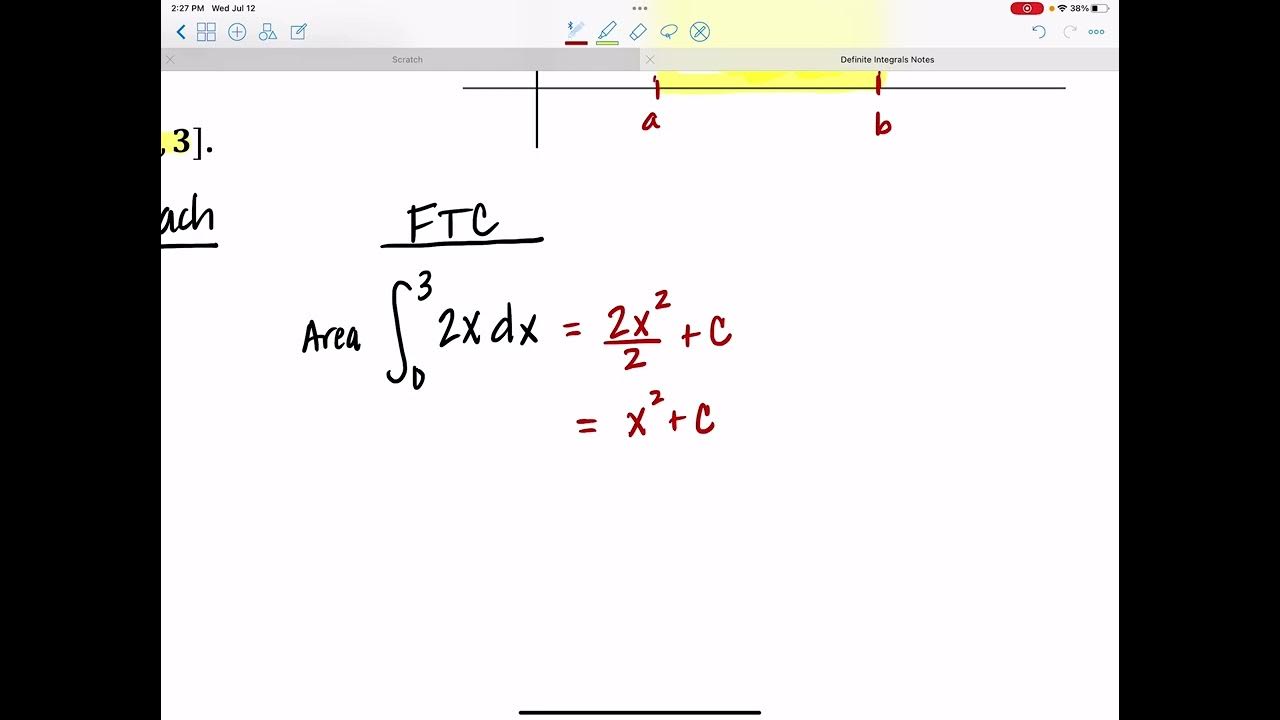
- 🔢 The antiderivative of a function is used to evaluate definite integrals, and it corresponds to the original function's rate of change.
- 📈 For a function like 3x + 2, the area under the curve can be found by breaking it down into fundamental shapes (rectangle and triangle) and summing their areas.
- 🏢 When encountering absolute value functions, the integral must be split into two parts, one for the positive and one for the negative values of x.
- 🤹♂️ The area of a semicircle can be found by taking half the area of a full circle, using the formula 1/2 * π * R^2, where R is the radius.
- 🔄 The process of evaluating definite integrals using geometry involves understanding the shape of the graph and breaking it down into recognizable geometric figures.
- 📚 It's important to apply the correct mathematical formulas when calculating the area of different shapes (rectangles, triangles, semicircles, etc.).
- 💡 The key to solving these problems is to combine the understanding of the antiderivative with the geometric interpretation of the function's graph.
Q & A
What is the main topic of the video?
-The main topic of the video is evaluating definite integrals using geometry.
How is the value of a definite integral related to the graph of a function?
-The value of a definite integral is related to the graph of a function as it represents the area of the shaded region bounded by the graph, the x-axis, and the given interval limits.
What is the first example's function and interval given in the video?
-The first example's function is y = 8 (a horizontal line) and the interval is from x = 1 to x = 4.
How is the area of the rectangle in the first example calculated?
-The area of the rectangle in the first example is calculated by multiplying the width (4 - 1 = 3) by the height (8), resulting in an area of 24 square units.
What is the antiderivative of the function 2x in the second example?
-The antiderivative of the function 2x is x squared divided by 2.
What is the area of the shaded region for the second example?
-The area of the shaded region for the second example is a right triangle with a base of 4 and a height of 8. The area is calculated as 1/2 base times height, which equals 1/2 * 4 * 8 = 16 square units.
How does the video describe the process of evaluating the definite integral of the function 3x + 2?
-The video describes the process by first identifying the fundamental shapes (a rectangle and a triangle) that make up the shaded region, determining the dimensions of each shape, calculating their areas, and then summing these areas to find the value of the integral.
What is the method used to evaluate the definite integral of the absolute value function in the video?
-The method used to evaluate the definite integral of the absolute value function is to break the graph into two parts (for positive and negative x values), write two separate functions for each part, and then integrate each part over the given interval.
What is the area of the shaded region for the absolute value function example?
-The area of the shaded region for the absolute value function example is a combination of a rectangle and a triangle. The rectangle has a base of 4 and a height of 1, and the triangle has a base of 4 and a height of 2. The total area is 4 + (1/2 * 4 * 2) = 4 + 4 = 8 square units.
How is the definite integral of the semicircle function evaluated in the video?
-The definite integral of the semicircle function is evaluated by recognizing that the function represents the upper half of a circle with radius 4. The area of a semicircle is 1/2 * π * R^2, so the integral is calculated as 1/2 * π * 4^2 = 8π square units.
What is the key takeaway from the video regarding the relationship between geometry and definite integrals?
-The key takeaway from the video is that geometry can be used to visually represent and calculate the value of definite integrals by finding the area of the shaded region bounded by the function's graph and the given interval on the x-axis.
Outlines
📊 Evaluating Definite Integrals Using Geometry
The paragraph begins with an introduction to the concept of evaluating definite integrals using geometric principles. The first example involves finding the value of a definite integral where the function is a horizontal line y=8 over the interval [1,4]. The explanation includes graphing the function, identifying the shaded region whose area represents the value of the integral, and calculating this area. The process is demonstrated by finding the area of a rectangle with width (4-1) and height 8, resulting in an area of 24 square units. This is confirmed by evaluating the antiderivative of the function, 8x, over the given interval. The second example involves the function 2x and its graph from [0,2], leading to the calculation of the area of a right triangle with base 4 and height 8, resulting in an area of 16 square units. This is again confirmed by evaluating the antiderivative, x^2/2, from 0 to 2. The paragraph concludes with a brief mention of a third example involving the function 3x+2, emphasizing the need to identify key points for the graph and the importance of the y-values at specific x-values.
📐 Breaking Down Composite Shapes for Area Calculation
This paragraph delves into the process of evaluating definite integrals for more complex functions by breaking them down into simpler geometric shapes. The example given involves the function 3x+2 and its graph from [1,5]. The task is to find the area of the shaded region, which is a combination of a rectangle and a triangle. The dimensions of these shapes are calculated, with the rectangle having a width of 4 and a height of 5, resulting in an area of 20 square units, and the triangle having a base of 4 and a height of 12, resulting in an area of 24 square units (after applying the 1/2 factor for triangle area calculation). The sum of these areas, 44 square units, is then confirmed by evaluating the antiderivative of the function, 3x^2/2 + 2x, over the interval [1,5]. The paragraph proceeds to explain how to handle absolute value functions in definite integrals, using the function 3 - |x| as an example. The graph of this function is described as a V-shape, and the process of evaluating the integral from -2 to 2 is outlined, emphasizing the need to split the integral into two parts and evaluate them separately.
🔢 Dealing with Absolute Value Functions and Semicircles
The paragraph focuses on evaluating definite integrals for functions involving absolute values and those representing semicircles. The first part of the paragraph explains how to handle the absolute value function 3 - |x| by splitting the integral into two separate functions, one for the left side of the graph (3 + x) and one for the right side (3 - x), and evaluating them over the interval from -2 to 2. The process is demonstrated step by step, leading to the same result as the geometric calculation. The second part of the paragraph addresses the evaluation of a definite integral for a function that represents a semicircle, derived from the standard equation of a circle. The process involves recognizing the function as representing the upper half of a circle (a semicircle) and using the formula for the area of a semicircle to calculate the shaded region's area. The radius of the circle is determined to be 4, and the area of the semicircle is calculated as half of the full circle's area, resulting in an area of 8π square units.
Mindmap
Keywords
💡Definite Integral
💡Graphing Function
💡Antiderivative
💡Area Calculation
💡Fundamental Theorem of Calculus
💡Slope-Intercept Form
💡Right Triangle
💡Composite Shape
💡Absolute Value Function
💡Semicircle
💡Standard Equation of a Circle
Highlights
The video focuses on evaluating definite integrals using geometry.
The value of a definite integral is the area of the shaded region under a horizontal line.
For the function y = 8, the interval of interest is from x = 1 to x = 4.
The area of the rectangle is calculated as width times height, yielding 24 square units.
The antiderivative of a constant function, like 8x, is the constant times x.
The antiderivative of 2x is x^2; the area of the right triangle is 16 square units.
For the function 3x + 2, the integral is evaluated by breaking the graph into a rectangle and a triangle.
The area of the composite shape (rectangle + triangle) is 44 square units.
The antiderivative of 3x + 2 is 3x^2/2 + 2x; the integral confirms the area is 44 square units.
For the function 3 - |x|, the integral is evaluated by breaking the graph into two parts, one for positive x and one for negative x.
The area of the shaded region for the absolute value function is 8 square units.
The definite integral of the absolute value function is split into two parts and evaluated separately for positive and negative x.
The function x^2 + y^2 = 16 represents a circle with radius 4.
The area of the shaded region for the semicircle is 8π square units.
Geometry is used to evaluate definite integrals when conventional techniques are not applicable.
Understanding the shape represented by a function is crucial for using geometry to evaluate definite integrals.
The video demonstrates the process of evaluating definite integrals using geometric shapes and their areas.
The method of breaking down a composite shape into fundamental shapes is a key technique for evaluating definite integrals using geometry.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: