Fundamental Theorem of Calculus Part 2

The Organic Chemistry Tutor
10 Mar 201811:23
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the second part of the Fundamental Theorem of Calculus, explaining how to evaluate definite integrals using anti-derivatives. It provides step-by-step examples, including the integration of polynomials and functions with constant multiples, as well as more complex integrals involving square roots and fractional exponents. The explanation is clear, methodical, and aims to solidify the viewer's understanding of calculus principles.

Takeaways
  • 📚 The video discusses the second part of the Fundamental Theorem of Calculus, which is essential for evaluating definite integrals.
  • 🌟 A function f must be continuous on the closed interval [a, b] for the theorem to apply, with F as the antiderivative of f.
  • 🔍 The definite integral of f(x) from a to b is given by the difference F(b) - F(a), as per the theorem.
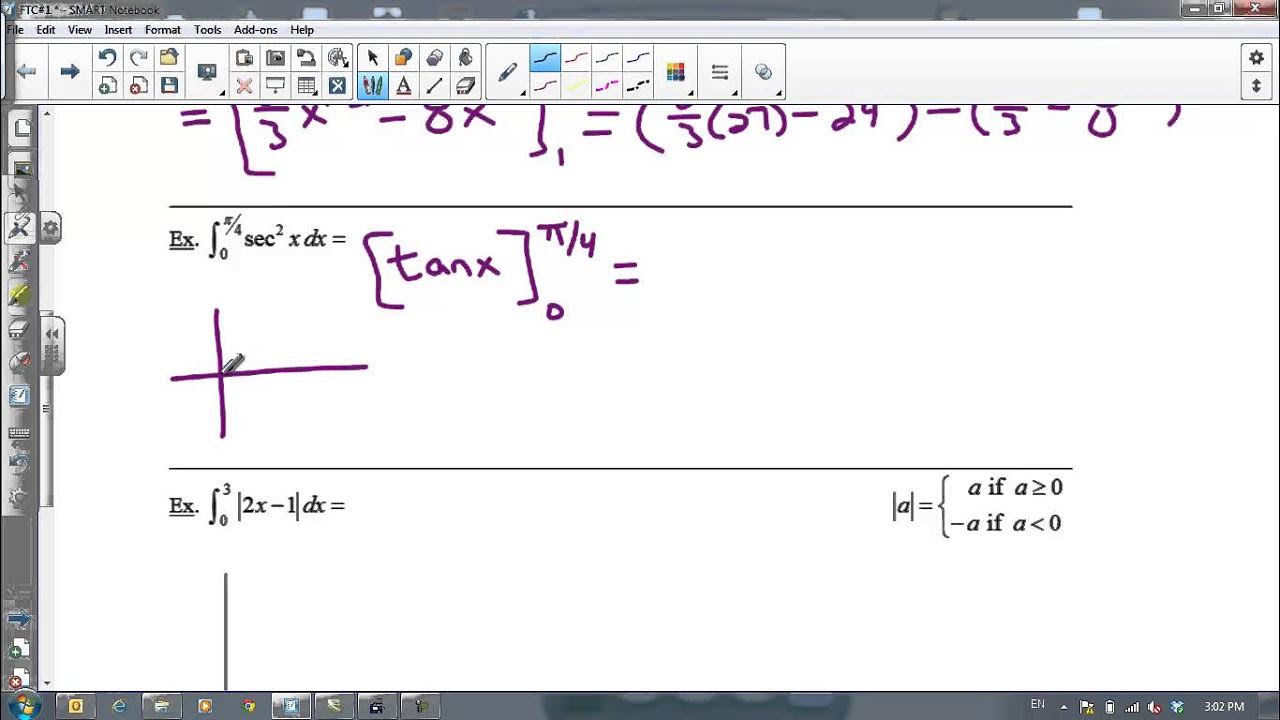
  • 🧩 Example 1: The antiderivative of 3x is (3x^2)/2, and the integral from 2 to 5 yields a final answer of 39/2.
  • 🧩 Example 2: The integral of (2x - 3)(2x - 3) is simplified to 4x^2 - 12x + 9, and evaluated from 1 to 4, resulting in 21.
  • 🧩 Example 3: The integral of √5/x is rewritten as 2√5 * x^(-1/2), and evaluated from 1 to 4, yielding 2√5.
  • 🧩 Example 4: The integral of (1/4)(x + √x) is simplified to (1/4)(x^2/2 + x^(3/2)/3), and evaluated from 0 to 1, resulting in 7/24.
  • 📈 The process of evaluating integrals involves finding antiderivatives, applying the power rule, and computing definite integrals.
  • 🔑 The power rule is a crucial tool for finding antiderivatives of polynomial functions.
  • 📊 The examples demonstrate the importance of understanding how to combine like terms and find common denominators in the process of integration.
  • 📋 The video script serves as a comprehensive guide for students learning the application of the Fundamental Theorem of Calculus in solving integrals.
Q & A

  • What is the main topic discussed in the video?

    -The main topic discussed in the video is the second part of the Fundamental Theorem of Calculus.

  • What does the second part of the Fundamental Theorem of Calculus state?

    -The second part of the Fundamental Theorem of Calculus states that the definite integral of a function f(x) on the interval [a, b] is equal to the difference between the values of the antiderivative F(x) evaluated at b and a, i.e., ∫[a, b] f(x) dx = F(b) - F(a).

  • What is an anti-derivative of a function?

    -An anti-derivative of a function is a function F(x) such that the derivative of F(x) with respect to x is the given function f(x). In other words, F'(x) = f(x).

  • How does the video demonstrate the application of the Fundamental Theorem of Calculus?

    -The video demonstrates the application of the Fundamental Theorem of Calculus by solving several examples of definite integrals using the theorem. It shows the process of finding the antiderivative of the integrand and then evaluating it at the endpoints of the interval to find the integral.

  • What is the first example given in the video to illustrate the theorem?

    -The first example given in the video is the integral of the function 3x + 4 from 2 to 5. The antiderivative is found using the power rule, and then the theorem is applied to find the definite integral.

  • How is the integral of 3x + 4 evaluated from 2 to 5?

    -The integral is evaluated by first finding the antiderivative of 3x, which is (3x^2)/2, and the antiderivative of 4, which is 4x. Then, using the Fundamental Theorem of Calculus, the definite integral is calculated as F(5) - F(2) = [(3*(5^2))/2 - 4*5] - [(3*(2^2))/2 - 4*2].

  • What is the result of the integral of 3x + 4 from 2 to 5?

    -The result of the integral is 39/2, which simplifies to 19.5.

  • What is the second example worked out in the video?

    -The second example is the integral of the expression (2x - 3)(x - 3) from 1 to 4. The example involves expanding the expression, finding the antiderivative, and then applying the Fundamental Theorem of Calculus to find the definite integral.

  • How is the expression (2x - 3)(x - 3) expanded?

    -The expression is expanded by multiplying the two binomials: (2x - 3)(x - 3) = 2x^2 - 6x - 3x + 9, which simplifies to 2x^2 - 9x + 9.

  • What is the antiderivative of 2x^2 - 9x + 9?

    -The antiderivative of 2x^2 - 9x + 9 is (2x^3)/3 - (9x^2)/2 + 9x, considering the power rule for integration and the fact that a constant can be moved outside the integral.

  • What is the final answer for the integral of (2x - 3)(x - 3) from 1 to 4?

    -The final answer for the integral is 21.

  • What is the third example discussed in the video?

    -The third example is the integral of √(5/x) from 1 to 4. The example involves rewriting the integrand and applying the power rule for integration.

  • How is the integral of √(5/x) evaluated from 1 to 4?

    -The integral is evaluated by rewriting the expression as (√5)/√x and then using the power rule to find the antiderivative, which is 2√5 * (√x)^(-1). The definite integral is then calculated by substituting the values of x = 4 and x = 1 into the antiderivative and finding the difference.

  • What is the result of the integral of √(5/x) from 1 to 4?

    -The result of the integral is 2√5.

  • What is the final example solved in the video using the Fundamental Theorem of Calculus?

    -The final example is the integral of (4/x + √x) from 0 to 1. The example involves separating the constant term, applying the power rule for integration, and then evaluating the antiderivative at the interval endpoints.

  • What is the antiderivative of x + √x?

    -The antiderivative of x + √x is (x^2)/2 + (2/3)x^(3/2), found by applying the power rule for both terms.

  • What is the final answer for the integral of (4/x + √x) from 0 to 1?

    -The final answer for the integral is 7/24.

Outlines
00:00
📚 Introduction to the Fundamental Theorem of Calculus

This paragraph introduces the second part of the Fundamental Theorem of Calculus, which is essential for understanding how to evaluate definite integrals. It explains that given a continuous function f on a closed interval [a, b], and F as the antiderivative of f, the definite integral of f(x) from a to b is equal to F(b) - F(a). The explanation is supported by an example where the anti-derivatives of 3x and 4 are found using the power rule, and then used to evaluate the integral from 2 to 5. The calculations are shown step-by-step, leading to a final answer of 39/2.

05:01
🧠 Working with Polynomial Functions and Integration

The second paragraph delves into evaluating more complex integrals using the Fundamental Theorem of Calculus. It starts by expanding the product (2x - 3)(x - 3), resulting in a polynomial function 4x^2 - 12x + 9. The antiderivative F(x) is then found by applying the power rule and integrating constants. The definite integral from 1 to 4 is evaluated next, with the result calculated in a step-by-step manner, leading to a final answer of 21.

10:02
🌟 Evaluating Definite Integrals with Non-Polynomial Functions

The final paragraph discusses the evaluation of definite integrals involving non-polynomial functions. It begins with the integral of √(5/x) from 1 to 4, which is simplified by separating the constant and rewriting the expression using exponents. The power rule is applied to find the antiderivative, and the integral is evaluated, resulting in a final answer of 2√5. The paragraph concludes with another example where a constant is factored out and the integral of x + √x is evaluated, leading to a final result of 7/24.

Mindmap
Keywords
💡Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus is a foundational result in calculus that connects the process of differentiation with integration. It states that if a function is continuous on a closed interval [a, b], and F is an antiderivative of f on that interval, then the definite integral of f from a to b is equal to F(b) - F(a). This theorem is crucial for evaluating definite integrals and has wide applications in various fields of mathematics, physics, and engineering. In the video, the theorem is used to solve several integral problems, demonstrating its practical application in calculating areas and volumes.
💡Anti-derivative
An anti-derivative, also known as an indefinite integral, is a function whose derivative is a given function. In the context of the video, finding the anti-derivative of a function is a necessary step before applying the Fundamental Theorem of Calculus to evaluate definite integrals. The process involves using integration rules, such as the power rule, to find the function that, when differentiated, yields the original function.
💡Definite Integral
A definite integral represents the signed area under a curve within a specified interval. It is a fundamental concept in calculus used to calculate quantities such as the displacement of an object, the work done by a force, or the area of a shape. The value of a definite integral is found by evaluating the antiderivative of the function at the endpoints of the interval and subtracting the results. The video script demonstrates the process of evaluating definite integrals using the Fundamental Theorem of Calculus.
💡Closed Interval
A closed interval is a set of numbers on the real number line that includes both its endpoints. In the context of the video, the closed interval [a, b] is the range over which the function is being integrated. The Fundamental Theorem of Calculus applies to functions that are continuous on such intervals, allowing the calculation of definite integrals.
💡Power Rule
The power rule is a basic integration technique in calculus that allows the integration of a function of the form x^n, where n is any real number. According to the power rule, the integral of x^n is (x^(n+1))/(n+1) + C, where C is the constant of integration. This rule is essential for finding anti-derivatives of polynomial functions and is used in the video to find the anti-derivatives of functions like 3x and 4x.
💡Integration
Integration is a fundamental process in calculus that involves finding the anti-derivative of a function, which can be used to compute the area under a curve, the volume of a solid, or the accumulated quantity in various physical and mathematical problems. In the video, integration is performed using the Fundamental Theorem of Calculus and various integration techniques, such as the power rule, to solve for definite integrals.
💡Constant
In the context of calculus, a constant is a value that does not change. When integrating a function that includes constants, the constant can be factored out and multiplied by the integral of the remaining function. The constant is then multiplied by the antiderivative of the function, which is an important aspect when applying the Fundamental Theorem of Calculus.
💡Common Denominators
Finding common denominators is a process in algebra and calculus that involves expressing fractions with different denominators as equivalent fractions with the same denominator. This is often necessary when adding or subtracting fractions, as it allows for the combination of terms into a single fraction. In the video, the process of finding common denominators is used to combine fractions when evaluating definite integrals.
💡Rationalization
Rationalization is the process of eliminating the radical, or root, from the denominator of a fraction. This is often done by multiplying both the numerator and the denominator by a suitable expression that contains the conjugate of the denominator. In the context of the video, rationalization is not explicitly mentioned but is a technique that could be used when integrating functions involving square roots or other radicals.
💡Substitution
Substitution is a technique used in integration to simplify the process by replacing parts of the integrand with other expressions. This often involves recognizing patterns or using algebraic identities to transform the function into a form that is easier to integrate. In the video, the technique of substitution is implied when the script rewrites expressions to make them easier to integrate using the power rule and other integration techniques.
💡Evaluation
In the context of the video, evaluation refers to the process of calculating the value of a function or an expression at specific points. This is essential when applying the Fundamental Theorem of Calculus, as it involves evaluating the antiderivative at the endpoints of the interval to find the definite integral.
Highlights

Introduction to the second part of the Fundamental Theorem of Calculus.

Explanation that the theorem applies to a function f that is continuous on the closed interval a to b.

The anti-derivative of f, denoted as capital F, is used to evaluate the definite integral.

The definite integral of f(x) from a to b is equal to F(b) - F(a).

Example given: finding the anti-derivative of 3x and evaluating it from 2 to 5.

Detailed calculation of the integral of 3x from 2 to 5, resulting in the answer 39/2.

Another example: evaluating the integral of (2x - 3)(2x - 3) from 1 to 4.

Explanation of the process to find the anti-derivative of the given polynomial expression.

The final answer for the polynomial integral is derived as 21.

An example of finding the integral of √5/x from 1 to 4 is discussed.

Rewriting the expression to isolate the variable and constant for easier integration.

The integral is evaluated, resulting in the final answer of 2√5.

A final example is presented, involving the integral of (4x + √x) from 0 to 1.

The anti-derivatives for x and √x are found and used to evaluate the integral.

The conclusion of the video with the integral's result of 7/24.

The video provides a comprehensive overview of applying the Fundamental Theorem of Calculus to various integrals.

The importance of understanding the relationship between anti-derivatives and definite integrals is emphasized.

Practical applications of the theorem are demonstrated through multiple examples.

Transcripts

Browse More Related Video

AP Calculus AB: Lesson 6.6 Fundamental Theorem of Calculus, Part 2

Definite Integral

Fundamental Theorem of Calculus

Antiderivatives and Indefinite Integrals

Improper Integrals - Discontinuity at a Boundary

2012 AP Calculus: AB FRQ Solutions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusIntegralsAnti-DerivativesMathematicsEducationalTheoreticalTutorialContinuous FunctionsClosed Intervals