Derivatives (part 9)

Khan Academy
4 Oct 200709:56
EducationalLearning
32 Likes 10 Comments

TLDRThe video script is an engaging and informative walkthrough of various calculus problems involving derivatives. It emphasizes the importance of practice and the mechanical nature of derivative calculations. The script covers the application of chain and product rules, and demonstrates solving complex derivative problems with examples like sin(3x) + 2x, e^x*cos(x^5), ln(x/(3x+10)), and p = sin(x)/cos(x). The explanations are clear, and the process is broken down into manageable steps, making the content accessible and educational for learners.

Takeaways
  • 📚 Derivatives are best learned through practice and exposure.
  • 🔄 The chain rule is applied when differentiating composite functions.
  • 📈 The derivative of sin(3x^5 + 2x) is found by using the chain rule and multiplying the derivative of the inside function by the derivative of the outside function.
  • 🌀 For the function y = e^x * cos^5(x), the product rule and chain rule are used to find dy/dx, highlighting the importance of understanding the derivatives of basic functions like e^x and cos(x).
  • 🔢 The derivative of e^x is e^x itself, a fundamental result in calculus.
  • 📊 The quotient rule can be conceptualized as a product rule, simplifying the process of differentiating complex expressions involving division.
  • 📐 The derivative of natural log(x) is 1/x, which is used in combination with the chain rule to differentiate more complicated expressions.
  • 📍 When differentiating p = sin(x)/cos(x), the result can be simplified using trigonometric identities, leading to the conclusion that the derivative of tan(x) is sec^2(x).
  • 🎓 The process of differentiation is essentially algebraic manipulation, requiring a good understanding of basic rules and functions.
  • 🚀 With a solid grasp of the chain and product rules, students are equipped to tackle a wide range of derivative problems in calculus.
Q & A

  • What is the main focus of the transcript?

    -The main focus of the transcript is to discuss the application of the chain and product rules in calculus for finding derivatives of various functions.

  • What is the derivative of the function f(x) = sin(3x^5) + 2x?

    -The derivative of the function f(x) = sin(3x^5) + 2x is f'(x) = 15x^4 * cos(3x^5) + 2.

  • How does the chain rule apply to the example of e^x * cos^5(x)?

    -The chain rule applies by taking the derivative of e^x, which is e^x, and multiplying it by the derivative of cos^5(x), which requires using the chain rule again for the cosine function.

  • What is the derivative of the natural log function with respect to x?

    -The derivative of the natural log function with respect to x is 1/x.

  • What is the quotient rule, as mentioned in the transcript?

    -The quotient rule, as mentioned in the transcript, is equivalent to the product rule and is used to find the derivative of a function that is the quotient of two other functions.

  • What is the derivative of p(x) = sin(x) / cos(x)?

    -The derivative of p(x) = sin(x) / cos(x) is p'(x) = (cos(x)^2 - sin(x)^2) / (cos(x))^2, which simplifies to cot^2(x).

  • How does the product rule help in simplifying derivatives?

    -The product rule helps in simplifying derivatives by breaking down complex functions into simpler components, allowing for easier calculation of the derivative by multiplying the derivative of one part by the other part and vice versa.

  • What is the significance of the derivative of e^x?

    -The significance of the derivative of e^x is that it is equal to the original function e^x itself, which is a fundamental property in calculus and an example of an exponential function's behavior under differentiation.

  • What trigonometric identity is used in the last example of the transcript?

    -The trigonometric identity used in the last example of the transcript is the relationship between the derivative of the tangent function and the secant function, where the derivative of tan(x) is equal to sec^2(x).

  • How does the transcript emphasize the importance of practice in learning derivatives?

    -The transcript emphasizes the importance of practice in learning derivatives by encouraging the learner to apply the chain and product rules as much as possible, highlighting that derivatives are about exposure and practice, and that with enough practice, the process becomes more mechanical and easier than it initially appears.

  • What is the purpose of changing notations in the examples?

    -The purpose of changing notations in the examples is to help the learner get used to various notations that can be used in calculus, making them more adaptable and comfortable with different ways of representing the same mathematical concepts.

Outlines
00:00
📚 Introduction to Derivatives and Practice

This paragraph introduces the concept of derivatives and emphasizes the importance of practice in understanding and applying them. It explains that derivatives can be approached using the chain and product rules, and encourages learners to practice regularly. The paragraph presents a specific function, f(x) = sin(3x)^5 + 2x, and demonstrates how to find its derivative using the chain rule. It highlights that while derivatives may initially seem abstract, they are actually a mechanical process and easier than other mathematical concepts once understood.

05:00
🔍 Applying Chain and Product Rules

This paragraph delves deeper into the application of the chain and product rules for finding derivatives. It introduces a new function, y = e^x * cos(x)^5, and explains how to break it down using the mentioned rules. The explanation includes taking the derivative of e^x, which is e^x itself, and then dealing with the second term, cos(x)^5, using the chain rule. The paragraph also discusses the derivative of cosine x, which is -sin x, and how to apply this in the context of the given function. It further simplifies the derivative expression and reinforces the idea that all the processes involved are essentially algebraic.

Mindmap
Keywords
💡Derivative
A derivative, in calculus, is a measure of how a function changes as its input changes. It is used to analyze the rate of change or the slope of a function at any point. In the video, the concept of derivatives is central to understanding the rate of change of various functions, such as sin(3x) and e^x, and how they relate to their respective inputs.
💡Chain Rule
The chain rule is a fundamental calculus technique used to find the derivative of a composite function. It states that the derivative of a function composed of other functions is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is applied to expressions like (sin(3x))^5 and e^(x)cos^5(x) to find their derivatives.
💡Product Rule
The product rule is a calculus formula used to find the derivative of a product of two or more functions. It states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function. The video emphasizes the product rule as a tool for differentiating complex expressions involving multiplication.
💡Practice
Practice, as emphasized in the video, is the process of repeatedly applying and refining one's understanding of a concept through application and exercise. In the context of derivatives, practice involves solving a variety of problems to gain proficiency in using calculus rules like the chain rule and product rule.
💡Mechanical
In the context of the video, 'mechanical' refers to the idea that the process of finding derivatives, while initially abstract, can become routine and systematic with enough practice. It suggests that the process of differentiation follows a set of rules and procedures that can be mastered over time.
💡Abstract
The term 'abstract' in the video refers to the conceptual nature of mathematical ideas that may not have a physical or tangible representation. It highlights the initial challenge in understanding the concept of derivatives, which may seem intangible or difficult to visualize.
💡Exposure
In the context of the video, 'exposure' refers to the experience and familiarity gained by repeatedly encountering and working with a subject or concept. It is used to describe the process of becoming comfortable with the methods and ideas involved in calculating derivatives.
💡Sin and Cosine
Sine (sin) and cosine (cos) are fundamental functions in trigonometry, often used to model periodic phenomena. In the video, these functions are used as part of the functions being differentiated, and their derivatives, cos and -sin respectively, are essential in applying the chain and product rules.
💡Natural Logarithm
The natural logarithm, denoted as ln(x), is the logarithm of x to the base e, where e is the mathematical constant approximately equal to 2.71828. It is a key concept in calculus, often used to model growth and decay processes. In the video, the natural logarithm is part of a function for which the derivative is being found.
💡Quotient Rule
The quotient rule is a calculus formula used to find the derivative of a quotient of two functions. It states that the derivative of a quotient is the derivative of the numerator times the denominator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. Although not explicitly mentioned in the video, the quotient rule is related to the product rule as both are used for differentiating composite functions.
💡Tangent and Secant
The tangent (tan) of an angle in a right triangle is the ratio of the opposite side to the adjacent side. The secant (sec) is the reciprocal of the cosine function. In the context of the video, these concepts are used to illustrate the relationship between derivatives and trigonometric identities, specifically showing that the derivative of the tangent function is equal to the secant squared.
Highlights

The importance of practice in mastering derivatives is emphasized.

Derivatives can be seen as a mechanical process that is easier than many other mathematical concepts.

The chain rule is applied to find the derivative of a function involving sin(3x^5) + 2x.

The derivative of sin is identified as cosine, which is a fundamental concept in calculus.

A complex function involving e^x and cosine is broken down using the product and chain rules.

The derivative of e^x is e^x, which is described as an amazing mathematical fact.

The derivative of the function y = e^x * cos^5(x) is calculated using a combination of rules.

The quotient rule is equated to the product rule, simplifying the process of finding derivatives.

The natural log function and its derivative (1/x) are used in a problem involving a quotient.

The derivative of a function involving division is solved by converting it into a product rule problem.

The problem-solving process is described as algebraic manipulation, emphasizing the mathematical techniques involved.

The derivative of p = sin(x)/cos(x) is calculated, leading to a deeper understanding of trigonometric identities.

The final problem demonstrates that the derivative of the tangent function is equal to the secant squared, reinforcing the connection between derivatives and trigonometry.

The presentation concludes with an encouragement for further learning and practice in the next session.

The use of different colors to distinguish various notations and concepts is highlighted, aiding in understanding and retention.

The session emphasizes the practical application of the product, chain, and quotient rules in solving derivative problems.

The concept of derivatives as a measure of change is introduced, linking the theoretical with practical applications.

The session showcases the power of mathematical simplification and the beauty of elegant solutions.

Transcripts

Browse More Related Video

Applying the chain rule twice | Advanced derivatives | AP Calculus AB | Khan Academy

Quotient rule and common derivatives | Taking derivatives | Differential Calculus | Khan Academy

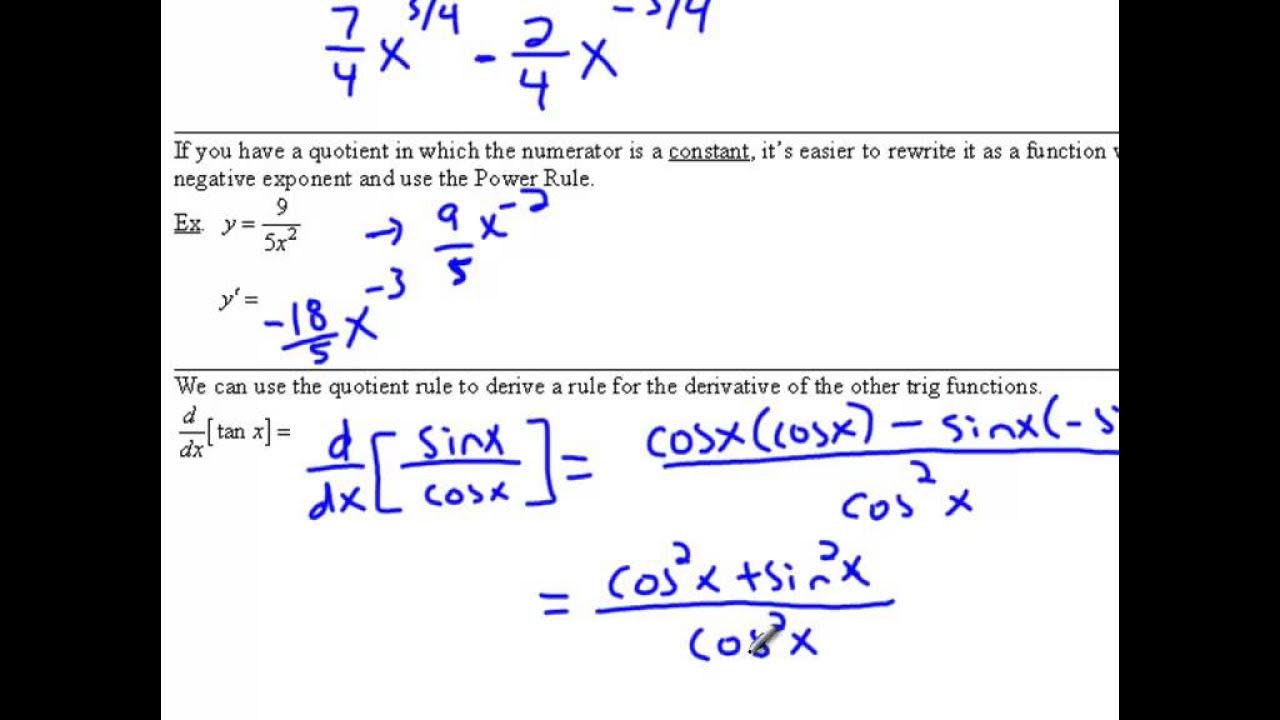
Product and Quotient Rule

BusCalc 13 Derivative Chain Rule

Derivatives of Logarithmic Functions - More Examples

Limits of Trigonometric Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Derivative RulesCalculus TutorialMath PracticeEducational ContentAbstract ConceptsAlgebraic SimplificationTrigonometric FunctionsExponential GrowthQuotient RuleProduct Rule