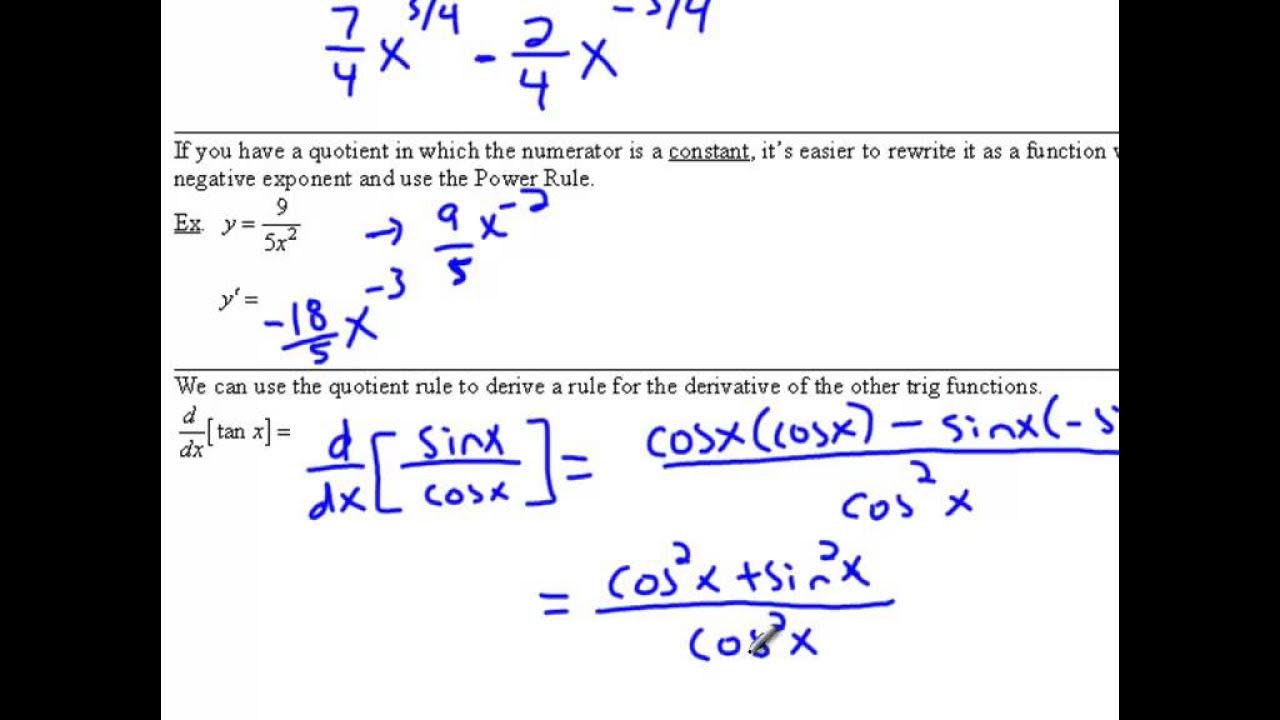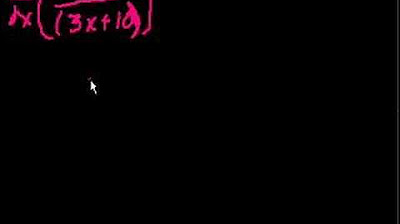Quotient rule and common derivatives | Taking derivatives | Differential Calculus | Khan Academy
TLDRThe video script discusses advanced derivative problems, emphasizing the product and chain rules for complex expressions. It simplifies the quotient rule by rewriting denominators as products. The video also highlights the remarkable derivatives of e^x (which is itself) and ln(x) (which is 1/x), as well as basic trigonometric functions like sin(x), cos(x), and tan(x). The content aims to deepen the understanding of calculus and inspire curiosity about mathematical functions and their derivatives.
Takeaways
- 📚 The main focus of the transcript is on understanding and solving derivative problems using calculus rules.
- 🌟 The quotient rule is described as a variation of the product rule with a negative exponent, and an alternative method is suggested for simplifying complex derivatives.
- 🔄 The chain rule is emphasized as a fundamental tool for taking derivatives of complex expressions, especially when dealing with exponents.
- 📈 The transcript provides a detailed example of how to apply the product and chain rules to a complex derivative problem involving a polynomial in both the numerator and the denominator.
- 🤯 The derivative of e^x is highlighted as a fascinating mathematical property, where the slope of the curve at any point is equal to the value of the function at that point.
- 🌿 The derivative of the natural logarithm (ln x) is noted as being 1/x, which is considered a remarkable and mind-blowing aspect of calculus.
- 📊 The transcript encourages the visualization of functions and their derivatives to gain a deeper understanding of the relationship between them.
- 📌 Basic trigonometric derivatives are introduced: the derivative of sin x is cos x, the derivative of cos x is -sin x, and the derivative of tan x is 1/cos²x or secant squared x.
- 💡 The importance of memorizing key derivatives is stressed for quick recall and application in solving calculus problems.
- 🚀 The presentation aims to build confidence in tackling a wide range of derivative problems, suggesting that mastery of these concepts can solve most problems encountered in an AP calculus exam.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the discussion of derivative problems in calculus, specifically focusing on the quotient rule, product rule, chain rule, and common derivatives of various functions.
How does the speaker feel about the quotient rule?
-The speaker finds the quotient rule to be mildly lame because it is just the product rule with a negative exponent and believes it clutters the brain.
What is the speaker's approach to finding the derivative of the given complex function?
-The speaker suggests rewriting the bottom expression as a product instead of using the quotient rule, and then applying the product rule along with the chain rule to find the derivative of the complex function.
What is the derivative of e to the x?
-The derivative of e to the x is e to the x. This means that at any point along the curve, the slope of that point is equal to the value of the function at that point.
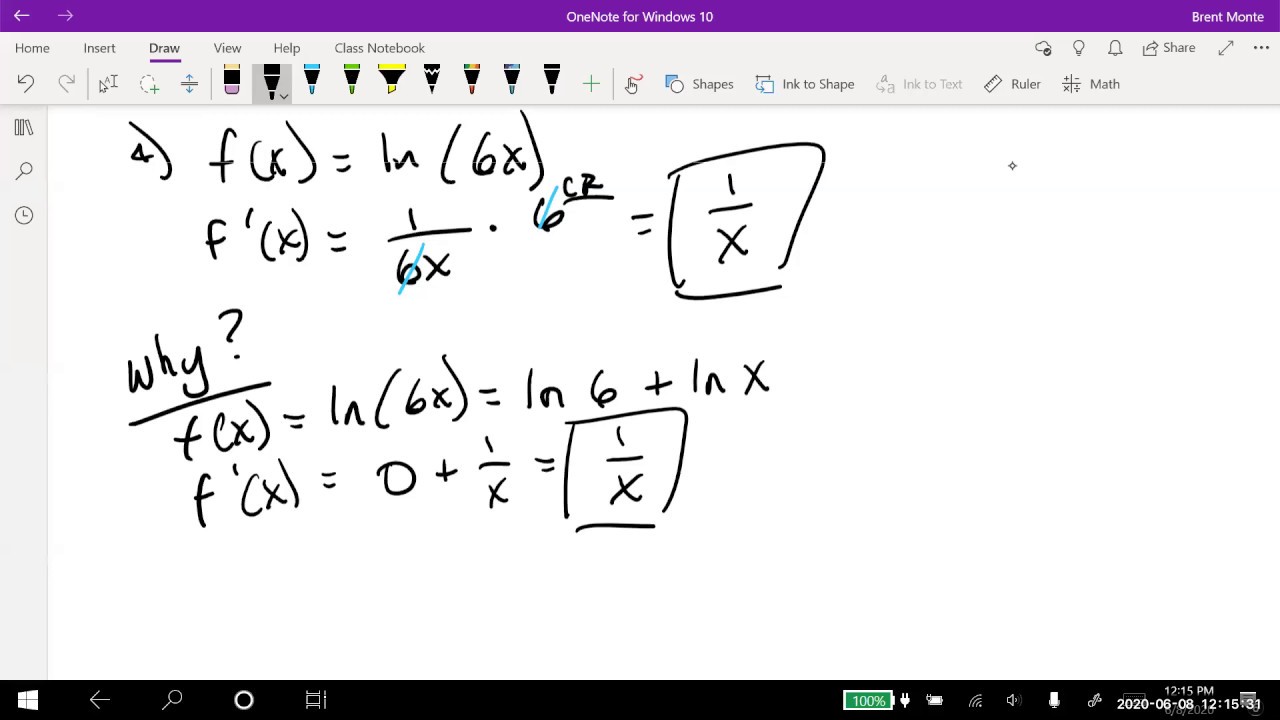
What is the derivative of the natural log of x?
-The derivative of the natural log of x is 1/x. This property is particularly fascinating because it fills the gap in the pattern of derivatives of powers of x.
What is the significance of the pattern observed in the derivatives of powers of x?
-The pattern observed in the derivatives of powers of x shows that the derivative of x to the n is n times x to the (n-1). However, there is no derivative for x to the -1 in this pattern, which is filled by the natural log function with a derivative of 1/x.
What are the derivatives of the basic trigonometric functions mentioned in the script?
-The derivative of sin(x) is cos(x), the derivative of cos(x) is -sin(x), and the derivative of tan(x) is 1/cos^2(x) or sec^2(x).
Why is it important to memorize these common derivatives?
-It is important to memorize these common derivatives to quickly recall and apply them in solving more complex derivative problems, especially during tests or real-world applications.
What advice does the speaker give for better understanding of derivatives?
-The speaker encourages viewers to explore these functions by graphing them and their derivatives to gain an intuitive understanding of why the derivative function describes the slope of the original function.
What is the speaker's plan for future presentations?
-The speaker plans to do more presentations exploring the magic of e, proving some of the derivatives mentioned, and using the product rule, chain rule, and other techniques to solve more complex derivative problems.
How can the concepts discussed in the script be applied to solve real-world calculus problems?
-The concepts discussed in the script, including the product rule, chain rule, and common derivatives, can be applied to solve a wide range of calculus problems, such as finding slopes of curves, optimizing functions, and modeling real-world phenomena.
Outlines
📚 Introduction to Derivative Problems and the Quotient Rule
This paragraph introduces the concept of derivative problems, focusing on a complex example involving a polynomial expression. The speaker explains the process of finding the derivative of a function, emphasizing the use of the product rule and chain rule instead of the quotient rule. The explanation includes a step-by-step breakdown of the derivative calculation for the given expression, highlighting the importance of understanding the underlying mathematical principles rather than relying on memorized rules. The speaker also encourages rewriting expressions to simplify the process and make it easier to apply the product and chain rules.
🤯 Mind-Blowing Derivatives of Exponential and Logarithmic Functions
In this paragraph, the speaker discusses the derivatives of exponential and logarithmic functions, highlighting their unique properties. The derivative of e to the power of x is e to the power of x, which the speaker finds particularly fascinating due to the constant slope equal to the function itself. The natural logarithm of x has a derivative of 1/x, which is also intriguing as it fits into a pattern of derivatives of power functions. The speaker emphasizes the importance of understanding these derivatives not just by memorization, but also by exploring and visualizing them through graphs and proofs. The paragraph concludes with a teaser for future presentations that will delve deeper into these concepts.
Mindmap
Keywords
💡derivative
💡quotient rule
💡product rule
💡chain rule
💡e to the x
💡natural log of x
💡trigonometric functions
💡slope
💡exponential functions
💡calculus AP test
Highlights
The introduction of a complex derivative problem involving a function with a numerator and a denominator.
The suggestion to rewrite complex expressions to simplify derivative calculations using the product rule instead of the quotient rule.
The explanation of how to apply the product and chain rules to find the derivative of the given complex expression.
The demonstration of the derivative calculation for the term (x^3 - 5x^5)^3.
The calculation of the derivative of the term (2x + 5)^(-5), emphasizing the importance of the chain rule and negative exponents.
The assertion that the product rule can be applied to a wide variety of problems, even those not initially recognized as fitting the rule's structure.
The introduction of common derivatives that are essential for understanding calculus.
The revelation that the derivative of e^x is itself, e^x, highlighting the unique and fundamental nature of the mathematical constant e.
The explanation of the derivative of the natural log of x, which is 1/x, and the discussion of its significance in the context of logarithms.
The observation of a pattern in the derivatives of exponential functions and the intriguing absence of a function with a derivative of x^(-1).
The identification of the natural log function as the derivative of x^(-1), which is a profound and unexpected result.
The presentation of basic trigonometric derivatives, including the derivatives of sin(x), cos(x), and tan(x).
The encouragement to memorize the derivatives of e^x, ln(x), and the basic trigonometric functions for solving calculus problems.
The suggestion to explore and graph these functions to gain a deeper understanding of derivatives and their relationship to the original functions.
The anticipation of future presentations that will apply these derivatives using the product and chain rules to solve more complex problems.
The emphasis on the ability to solve a majority of derivative problems on the calculus AP test with the knowledge shared in the presentation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: