Rewriting before integrating | AP Calculus AB | Khan Academy
TLDRThe video script demonstrates the power of algebraic simplification in evaluating indefinite integrals. It illustrates this by walking through the process of simplifying complex expressions, such as polynomials and radical expressions, before applying the reverse power rule to find the anti-derivatives. The examples provided show how distributing, dividing terms, and rewriting expressions can simplify the process of integration, emphasizing that sometimes the simplest techniques are the most effective.
Takeaways
- 🙂 Sometimes, the best technique for solving an integral is simple algebraic simplification.
- 📝 Distributing terms within an integral can transform it into a straightforward polynomial, making it easier to evaluate.
- 📚 The antiderivative of a polynomial can be found by incrementing the exponent by one and dividing by the new exponent.
- 💻 Algebraic simplification can involve dividing terms by a common denominator to simplify the expression before integration.
- 🙌 The reverse power rule is crucial for integrating terms with negative or fractional exponents.
- 💾 Incrementing the exponent by one and then dividing by that value allows for the integration of expressions with negative exponents.
- 💯 Rewriting expressions with roots as exponents (e.g., cube roots to one-third power) simplifies the integration process.
- 📈 Multiplying exponents when raising a power to another power is a fundamental property used in integration.
- 💎 For indefinite integrals, always remember to add the constant of integration, symbolized as +C.
- 🚀 The power rule for integration is validated by differentiation, where the original expression is retrieved by decrementing the exponent.
Q & A
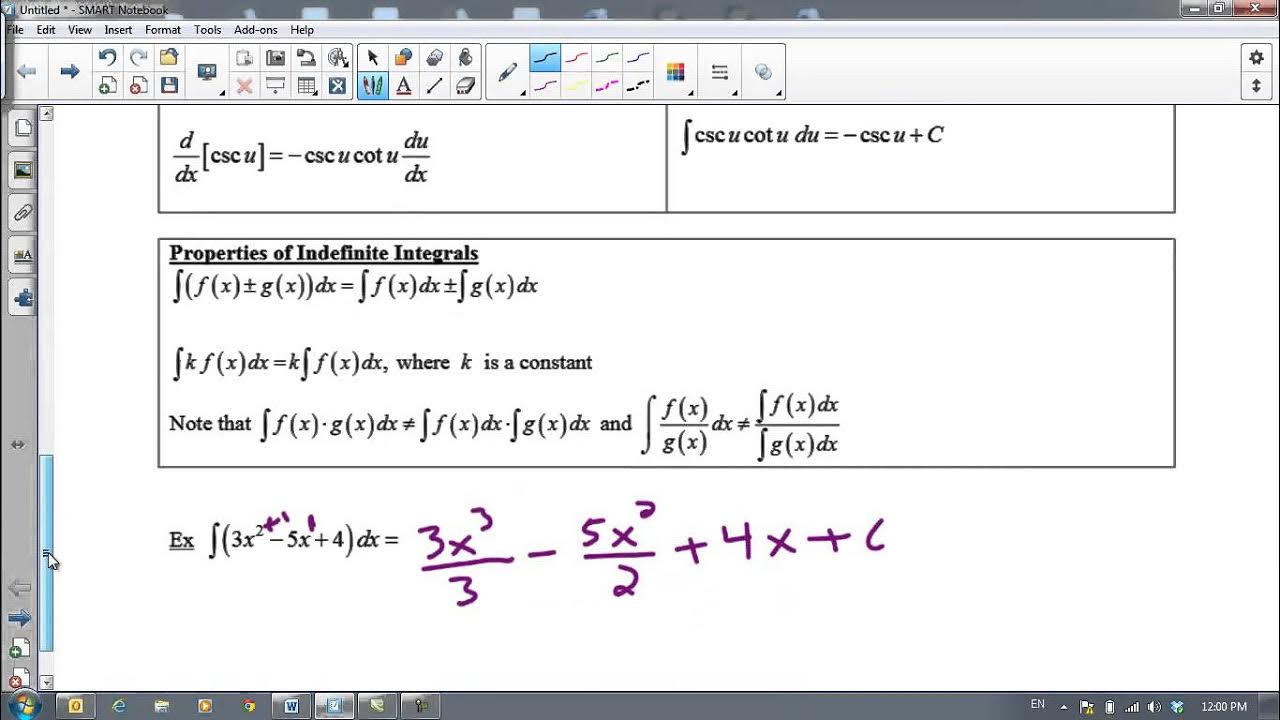
What is the indefinite integral of X squared times three X minus one DX?
-The indefinite integral of X squared times three X minus one DX is the anti-derivative of the polynomial, which can be found by distributing X squared and simplifying the expression. The result is the sum of the anti-derivatives of each term: three times X to the fourth over four, minus X to the third over three, plus a constant C.
What is the main technique used to simplify the indefinite integral of X squared times three X minus one DX?
-The main technique used is algebraic simplification. By distributing X squared and simplifying the expression, we can evaluate the anti-derivative more easily.
How do you simplify the expression X to the third plus three X squared minus five over X squared DX?
-You simplify the expression by dividing each term by X squared, which results in X, three, and negative five times X to the negative two power.
What is the indefinite integral of X to the third plus three X squared minus five over X squared DX?
-The indefinite integral is X squared over two plus three X plus negative five X to the negative one, plus a constant C.
How can the cube root of X to the fifth DX be rewritten for easier integration?
-The cube root of X to the fifth DX can be rewritten as X to the fifth to the one third, which simplifies to X to the five thirds DX, allowing for easier integration using the reverse power rule.
What is the indefinite integral of X to the five thirds DX?
-The indefinite integral is three eighths times X to the eight thirds, plus a constant C.
What is the reverse power rule used for in integration?
-The reverse power rule is used to find the anti-derivative of a function when the integrand is a power of the variable. It involves increasing the exponent by one and dividing by the new exponent.
How can you verify the correctness of an indefinite integral?
-You can verify the correctness of an indefinite integral by taking the derivative of the result and checking if it matches the original integrand.
What is the significance of including a constant C in an indefinite integral?
-The constant C is included in an indefinite integral to account for the arbitrary constant that arises from the antiderivative process, which is necessary because the derivative of a constant is zero.
What is the main takeaway from the video script regarding integration techniques?
-The main takeaway is that often the most powerful integration technique is to start with algebraic simplification. By simplifying the expression first, it becomes easier to apply integration rules and find the anti-derivative.
How does the power rule relate to integration?
-The power rule states that the integral of a power function, which is a function of the form f(x) = x^n, is given by (x^(n+1))/(n+1) + C, where n is a constant and C is the constant of integration.
Outlines
📚 Solving Indefinite Integrals through Algebraic Simplification
This paragraph introduces the concept of simplifying complex indefinite integrals through basic algebraic manipulation. The instructor presents an example where the indefinite integral of X squared times three X minus one DX is simplified by distributing X squared across the terms within the integral. The resulting polynomial is then integrated by applying basic anti-derivative rules, highlighting that sometimes the simplest techniques can be the most effective. The paragraph emphasizes the importance of algebraic simplification before attempting to evaluate complex integrals.
🎓 The Power of Algebraic Simplification in Integration
The second paragraph reinforces the main takeaway from the video, which is the power of algebraic simplification in solving integration problems. It emphasizes that before applying complex integration techniques, one should simplify the expression algebraically to a form that is easier to integrate. The paragraph serves as a reminder that even the most complicated integrals can often be simplified to a more manageable form through basic algebraic operations.
Mindmap
Keywords
💡indefinite integral
💡distribution
💡algebraic simplification
💡anti-derivative
💡power rule
💡cube root
💡exponent
💡constant
💡derivative
💡polynomial
💡simplify
Highlights
The importance of simplifying algebraic expressions before integrating was emphasized, which can make the process of finding the anti-derivative easier.
The technique of distributing X squared within the integral was demonstrated to simplify the expression and make it more manageable.
The integral of X squared times three X minus one DX was evaluated to show the process of distributing and simplifying the polynomial within the integral.
The anti-derivative of X to the third is X to the fourth over four, which was derived from the simplified expression.
The anti-derivative of X squared was found to be X to the third over three, which was part of the simplified integral.
The indefinite integral may include a constant, which was noted in the explanation.
The second example involved the indefinite integral of a complex expression involving X to the third, X squared, and a constant divided by X squared.
Algebraic simplification was again highlighted as the key to solving the second example by dividing each term by X squared.
The anti-derivative of X to the third divided by X squared simplifies to X.
Three X squared divided by X squared simplifies to three, which was part of the anti-derivative process.
Negative five divided by X squared simplifies to negative five times X to the negative two power.
The reverse power rule was used to find the anti-derivatives in the second example.
The third example involved the indefinite integral of the cube root of X to the fifth DX.
The cube root was rewritten as X to the fifth to the one third to simplify the integral.
The integral of X to the five thirds was found by using the reverse power rule and adjusting the exponents accordingly.
The final anti-derivative involved X to the eight thirds divided by three eighths, which simplifies to X to the five thirds as the solution.
The video concludes with the reminder that algebraic simplification is often the most powerful technique for integration.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: