BusCalc 13 Derivative Chain Rule

The video begins with an introduction to the derivative chain rule, a concept from calculus with applications in business. To understand the chain rule, the presenter reminds viewers of function composition from algebra, where one function is placed inside another. The analogy of a turkey with a chicken inside, popularized by a YouTube video, is used to illustrate this concept. Function composition involves identifying which function acts as the 'turkey' (outer function) and which as the 'chicken' (inner function). Several examples are provided to demonstrate how to compose functions and calculate the resulting function, such as f(g(x)) and g(f(x)), where f and g are defined as specific mathematical functions. The importance of correctly placing the inner function within the outer function is emphasized.

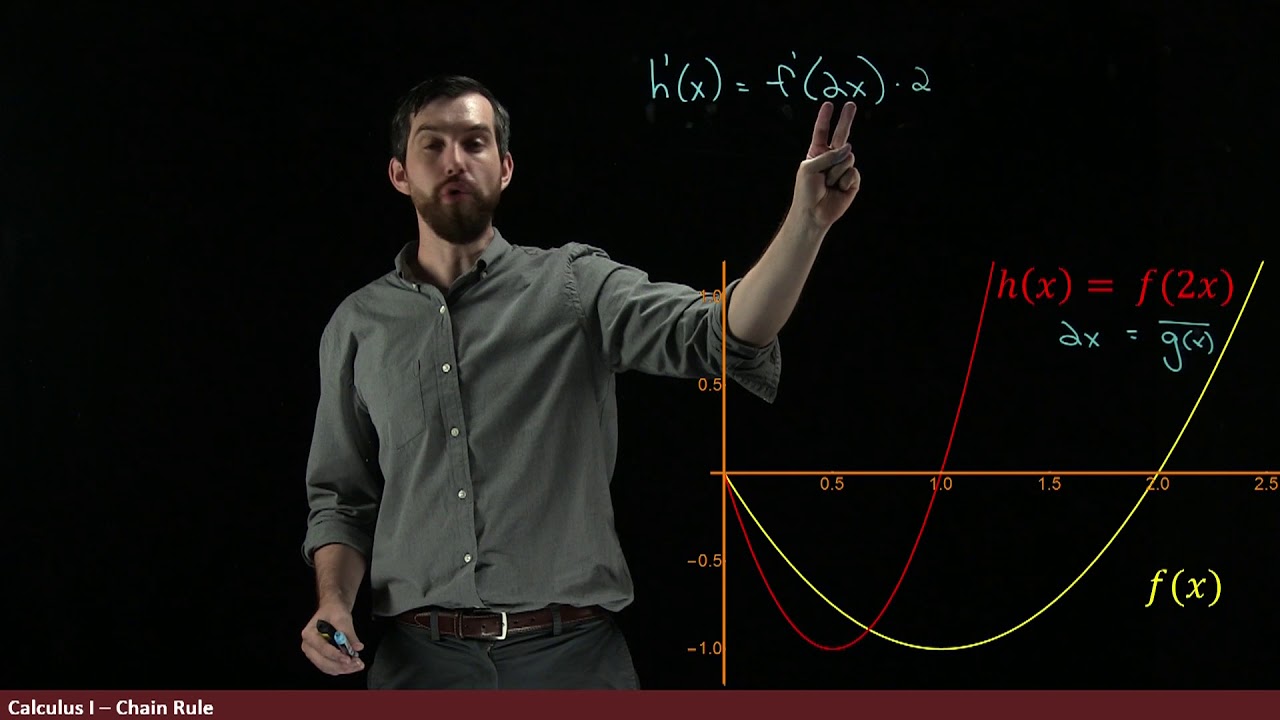
The presenter explains the derivative chain rule, which is a method to find the derivative of a function that is a composition of two simpler functions. The chain rule states that the derivative of the composed function (capital C) is the product of the derivative of the outer function (f') evaluated at the inner function (g(x)) and the derivative of the inner function (g'). The process involves identifying the outer and inner functions within the composition, applying the chain rule formula, and calculating the derivatives step by step. Examples include finding the derivative of a function defined as x to the fifth power composed with another function, as well as simplifying the expression further. The presenter also addresses different notations for representing the chain rule and encourages viewers to practice with multiple examples to gain proficiency.

The video script discusses an alternative notation for the chain rule, which involves a function u(x) that simplifies the process of finding derivatives. The presenter prefers this notation as it illustrates the concept of small changes in an intermediate function u, which cancel out when applying the chain rule. An example is given where the function y is expressed in terms of u, and the derivatives of y with respect to u and u with respect to x are calculated. The process concludes by substituting u back in terms of x to find the derivative dy/dx. The presenter emphasizes the importance of choosing a convenient function for u to facilitate the differentiation process.

The presenter applies the chain rule to a word problem involving the demand for a fidget toy as a function of its price. The demand function n is given in terms of the price p, and the task is to find the rate of change of demand with respect to price. To solve this, an intermediate variable u is introduced to simplify the derivative calculation. The function n is expressed in terms of u, and the derivatives of n with respect to u and u with respect to p are calculated. The chain rule is then applied to find the derivative of n with respect to p, which represents the rate of change of demand with respect to price. The presenter also calculates the demand when the price is three dollars, providing a numerical example of how to use the demand function.

The final paragraph focuses on finding the derivative of the demand function with respect to the price of a product. The presenter chooses an intermediate variable u to represent a part of the demand function that includes a square root, which simplifies the differentiation process. The derivative of the demand function n with respect to u is calculated first, followed by the derivative of u with respect to the price p. Applying the chain rule, the presenter multiplies these derivatives to find the rate of change of demand with respect to price. The final expression for the derivative is simplified and expressed in terms of the price p, illustrating how the chain rule can be used to solve for rates of change in real-world scenarios.