Limits of Trigonometric Functions
TLDRThis transcript discusses various limit problems involving trigonometric functions as x approaches 0. It explains how to confirm the limit of sin(x)/x as 1 by substituting values close to zero and demonstrates the use of substitution and known limit formulas to solve problems like the limit of sin(5x)/x and sin(2x)/5x. The process is also shown for more complex expressions, such as sin(7x)/sin(3x) and tan(x)/x, emphasizing the importance of showing work for a clear understanding of the concepts.
Takeaways
- 📈 The limit of sin(x)/x as x approaches 0 is 1, which can be confirmed by plugging in values close to 0 into a calculator.
- 🔢 For the limit of (1 - cos(x))/x as x approaches 0, the value is 0, demonstrated by plugging in small values like 0.1 and 0.01.
- 🌟 When calculating limits involving sin(nx)/x as x approaches 0, the answer is n, as shown by the example of sin(5x)/x yielding 5.
- 📚 To find the limit of sin(2x)/5x as x approaches 0, the process involves multiplying the numerator and denominator by 2/5 and simplification yields 2/5.
- 🔄 For limits involving sin(7x)/sin(3x) as x approaches 0, the result is 7/3 after separating and simplifying the expression using substitution.
- 🧭 The limit of tan(x)/x as x approaches 0 is 1, which can be deduced by rewriting tan(x) as sin(x)/cos(x) and applying known limits.
- 🔢 For the limit of tan(4x)/3x as x approaches 0, the answer is 4/3, following a similar process of substitution and simplification.
- ✅ The limit of (7 * (1 - cos(x)))/x as x approaches 0 is 0, since the limit of (1 - cos(x))/x is 0.
- 📐 The limit of sin^2(x)/x as x approaches 0 is 0, as sin(x)/x approaches 1 and x approaches 0, resulting in a product of 0.
- 🌀 For the limit of sin(x^2)/x as x approaches 0, the process involves multiplying the numerator and denominator by x and using substitution with y = x^2 to find the limit is 0.
Q & A
What is the value of the limit as x approaches 0 of sine x divided by x?
-The value of the limit as x approaches 0 of sine x divided by x is 1.
How can you confirm the limit using a calculator?
-You can confirm the limit by plugging in a number very close to 0 into the calculator, ensuring it's in radian mode, and then dividing the sine of that number by the number itself. As the input approaches zero, the result should approach the limit's value.
What is the formula for the limit as x approaches 0 of (1 - cosine x) divided by x?
-The formula for the limit as x approaches 0 of (1 - cosine x) divided by x is 0.
How does the value of the limit as x approaches 0 of (1 - cosine x) divided by x demonstrate its truth?
-By plugging in values close to 0, such as 0.1 and 0.01, and observing that the results approach 0, we can demonstrate that the limit as x approaches 0 of (1 - cosine x) divided by x is indeed 0.
What is the limit as x approaches 0 of sine 5x divided by x?
-The limit as x approaches 0 of sine 5x divided by x is 5. This is derived by multiplying the numerator and denominator by 5 and then using the known limit of sine x over x as x approaches 0, which is 1.
How can you evaluate the limit as x approaches 0 of sine 2x divided by 5x?
-The limit as x approaches 0 of sine 2x divided by 5x is 2 divided by 5 or 0.4. This is shown by multiplying the numerator and denominator by 2/2 and then using the known limit of sine x over x as x approaches 0.
What is the limit as x approaches 0 for sine 7x divided by sine 3x?
-The limit as x approaches 0 for sine 7x divided by sine 3x is 7 divided by 3. This is because when simplifying the expression and using the known limit of sine x over x as x approaches 0, the ratio of the coefficients (7 and 3) remains.
What is the value of the limit as x approaches 0 of tangent x divided by x?
-The value of the limit as x approaches 0 of tangent x divided by x is 1. Since tangent x is sine x divided by cosine x, and the limit of sine x over x as x approaches 0 is 1, and the limit of cosine x as x approaches 0 is 1, the result is 1.
How do you find the limit as x approaches 0 of tan 4x divided by 3x?
-The limit as x approaches 0 of tan 4x divided by 3x is 4 divided by 3. This is found by converting tangent to sine over cosine, multiplying the numerator and denominator by 4/4, and then using the known limit of sine x over x as x approaches 0.
What is the result of the limit as x approaches 0 of seven times one minus cosine x divided by x?
-The result of the limit as x approaches 0 of seven times one minus cosine x divided by x is 0. This is because the limit of one minus cosine x divided by x as x approaches 0 is 0, and any number times zero is zero.
How does the limit as x approaches 0 of sine squared x divided by x evaluate?
-The limit as x approaches 0 of sine squared x divided by x evaluates to 0. This is because sine squared x is sine x times sine x, and the limit of sine x over x as x approaches 0 is 1 while the limit of x as x approaches 0 is 0, resulting in 1 times 0, which is 0.
What is the limit as x approaches 0 of sine of x squared divided by x?
-The limit as x approaches 0 of sine of x squared divided by x is 0. This is found by multiplying the numerator and denominator by x to get the limit of sine x squared over x squared, and then using the limits as x approaches 0, which are 1 for sine x squared over x squared and 0 for x, resulting in 0.
Outlines
📚 Introduction to Trigonometric Limits
This paragraph introduces the concept of limits with trigonometric functions, focusing on the limit of sine x divided by x as x approaches 0, which is equal to 1. The explanation includes a practical technique using a calculator to approximate the limit by plugging in values close to zero. It also introduces another formula, the limit of (1 - cosine x) divided by x as x approaches 0, which equals 0, and demonstrates its confirmation through similar approximation methods.
🔢 Solving Trigonometric Limit Problems
The paragraph delves into solving specific trigonometric limit problems, such as the limit of sine 5x divided by x as x approaches 0, which simplifies to 5. It explains the process of substitution and demonstrates how to manipulate the expression to find the limit. The paragraph also covers the limit of sine 2x divided by 5x as x approaches 0, showing the steps to arrive at the answer of 2/5. Additionally, it touches on the limit of sine 7x divided by sine 3x as x approaches 0, which simplifies to 7/3, with a detailed explanation of the substitution and rearrangement of terms.
📈 Understanding Tangent and Sine Limits
This section discusses the limit of tangent x divided by x as x approaches 0, revealing that the answer is 1. It explains the relationship between tangent and sine/cosine, and how to apply the limit of sine x over x to find the solution. The paragraph also explores the limit of tan 4x divided by 3x as x approaches 0, confirming the answer as 4/3 through a step-by-step demonstration. Furthermore, it addresses the limit of (7 * (1 - cosine x)) divided by x as x approaches 0, which simplifies to 0, and the limit of sine squared x divided by x, which results in 0.
🧩 Advanced Trigonometric Limit Examples
The final paragraph presents more complex examples of trigonometric limits. It starts with the limit of sine of x squared divided by x as x approaches 0, which requires multiplying the numerator and denominator by x and using substitution to find the limit. The explanation then moves on to the limit of sine x squared divided by x, where the process involves separating the expression into two limits and simplifying to reach the answer of 0. The paragraph concludes with the limit of sine y divided by y times the limit of x as x approaches 0, which simplifies to 0, demonstrating the application of substitution and the properties of limits.
Mindmap
Keywords
💡Limits
💡Trigonometric Functions
💡Substitution
💡Direct Substitution
💡Sine Function
💡Cosine Function
💡Tangent Function
💡Calculator
💡Radian Mode
💡Factoring
💡Direct Calculation
Highlights
The limit of sine x divided by x as x approaches 0 is equal to 1.
Using a calculator in radian mode can confirm the limit by plugging in values close to 0, such as 0.1 and 0.01.
The limit of 1 minus cosine x divided by x as x approaches 0 is equal to 0.
Substitution technique involves multiplying the numerator and denominator by the same value to simplify the limit expression.
The limit of sine 5x divided by x as x approaches 0 can be found by multiplying the expression by 5 and using substitution.
The limit of sine 2x divided by 5x as x approaches 0 simplifies to 2 divided by 5 by using substitution and the known limit of sine x over x.
The limit of sine 7x divided by sine 3x as x approaches 0 is seven divided by three by separating the terms and using substitution.
The limit of tangent x divided by x as x approaches 0 is 1, as tangent is sine over cosine and the limit of sine x over x is 1.
For the limit of tan 4x divided by 3x as x approaches 0, the answer is 4 over 3, which is derived by converting tangent to sine over cosine and applying limits.
The limit of 7 times one minus cosine x divided by x as x approaches 0 is zero, as the limit of one minus cosine x divided by x is 0.
The limit of sine squared x divided by x as x approaches 0 is 0, by separating it into two limits and multiplying by 0.
The limit of sine of x squared divided by x as x approaches 0 is zero, using substitution and the fact that the limit of x as x approaches 0 is 0.
Trigonometric limits can be evaluated using direct substitution, calculator approximation, and substitution techniques.
Understanding the behavior of trigonometric functions near zero is crucial for solving limit problems.
The concept of limits allows us to determine the value a function approaches as the input gets arbitrarily close to a certain point.
The use of trigonometric identities and properties can simplify the process of finding limits.
The limit of a function can be found by breaking down complex expressions into simpler components.
The technique of substitution is particularly useful when dealing with trigonometric functions involving multiples of the variable.
The concept of limits is fundamental in calculus and is used to understand the behavior of functions at specific points.
Transcripts
Browse More Related Video
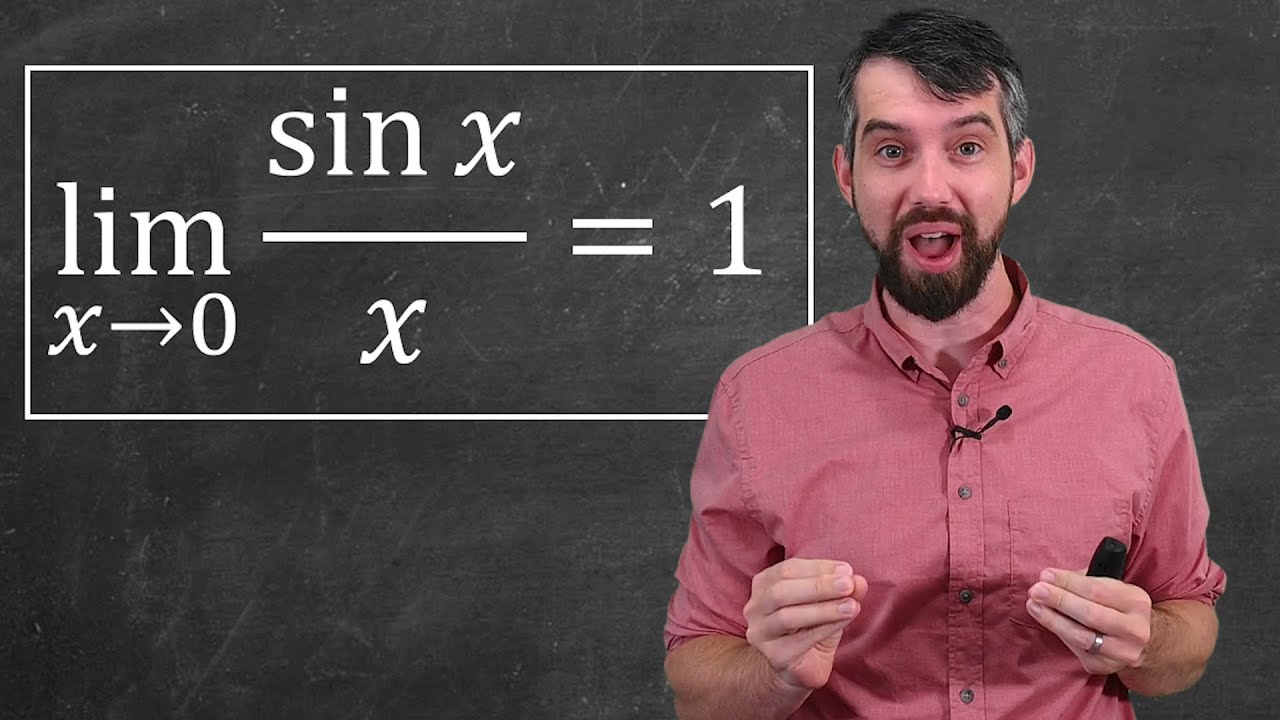
The most important limit in Calculus // Geometric Proof & Applications

Limit of (1-cos(x))/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy

Zero-Bounded Limit Theorem (with example)
Derivatives (part 9)

Quotient rule and common derivatives | Taking derivatives | Differential Calculus | Khan Academy
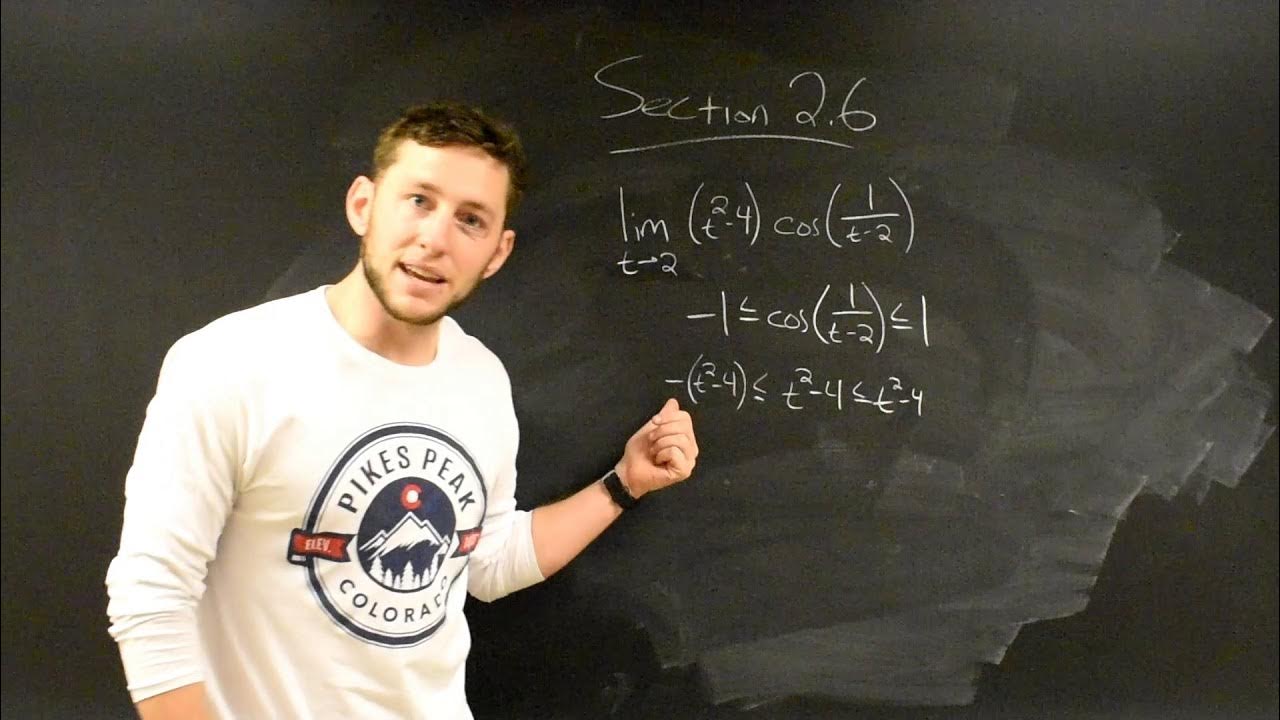
Limits Involving Sine and Cosine & The Squeeze Theorem!
5.0 / 5 (0 votes)
Thanks for rating: