Derivatives of Logarithmic Functions - More Examples
TLDRThis video script delves into the derivatives of logarithmic functions, focusing on essential formulas and their applications. It begins with the basic derivative of the natural logarithm, 'ln(x)', which is '1/x'. The script then expands on this by introducing the derivative of a more complex logarithmic function, 'ln(g(x))', emphasizing the use of the chain rule. It also covers the derivative of a logarithm with a different base, 'log_a(x)', which involves multiplying by the natural logarithm of the base. The video provides several examples to illustrate the application of these formulas, including the derivative of 'ln(x^2 + x)', '(ln(x))^(1/3)', 'ln(x^4 'cdot' sin(x))', and 'ln(x)/(1 + ln(2x))'. The script demonstrates the utility of logarithmic properties in simplifying derivative calculations, such as transforming 'ln(x^4 'cdot' sin(x))' into a sum of logarithms before differentiation. The video concludes with an encouragement for viewers to explore more examples and properties of logarithms on the presenter's website, offering help for any further questions.
Takeaways
- 📚 The derivative of \( \ln(x) \) is \( \frac{1}{x} \).
- 📈 For a more complex function \( \ln(g(x)) \), the derivative is \( \frac{1}{g(x)} \cdot g'(x) \), following the chain rule.
- 🔢 When dealing with a logarithm of a different base \( \log_a(x) \), the derivative is \( \frac{1}{x} \cdot \ln(a) \).
- 📘 For a generic logarithm \( \log_a(g(x)) \), the derivative involves \( \frac{1}{g(x)} \cdot g'(x) \cdot \ln(a) \).
- 📋 Remembering the two general formulas is crucial for deriving logarithmic functions.
- 🧮 Use standard differentiation rules (product, quotient, chain) after applying logarithmic derivative formulas.
- 🌟 Logarithms can simplify derivative calculations, as seen in the example \( \ln(x^4 \cdot \sin(x)) \).
- 📊 Rewriting expressions using logarithmic properties can make differentiation easier, as demonstrated with \( \ln(x^4) + \ln(\sin(x)) \).
- 📐 The derivative of \( \sqrt[3]{\log_7(x)} \) involves converting the root to a fractional exponent and applying the chain rule.
- 🤔 For quotients like \( \frac{\ln(x)}{1 + \ln(2x)} \), use the quotient rule to find the derivative.
- 🔁 Factoring and simplifying can help in cleaning up the derivative expressions, as shown in the final example.
Q & A
What is the derivative of the natural logarithm of x (Ln(x))?
-The derivative of the natural logarithm of x (Ln(x)) is 1/x.
How does the derivative of the logarithm of a function g(x) differ from the derivative of Ln(x)?
-The derivative of the logarithm of a function g(x), which is Ln(g(x)), involves the chain rule. It is given by (1/g(x)) multiplied by the derivative of g(x).
What is the formula for the derivative of a logarithmic function with a base other than e?
-The derivative of a logarithmic function with a base 'a' of x, which is log_a(x), is (1/(x * ln(a))) where ln(a) is the natural logarithm of the base 'a'.
How do you find the derivative of a more complex logarithmic function like log_a(g(x))?
-The derivative of log_a(g(x)) involves the chain rule and is given by (1/(g(x) * ln(a))) multiplied by the derivative of g(x).
What is the significance of knowing the four basic formulas for derivatives of logarithmic functions?
-Knowing the four basic formulas allows you to find the derivatives of a wide range of logarithmic functions. They are the foundation for applying more complex rules like the product rule, quotient rule, and chain rule to logarithmic expressions.
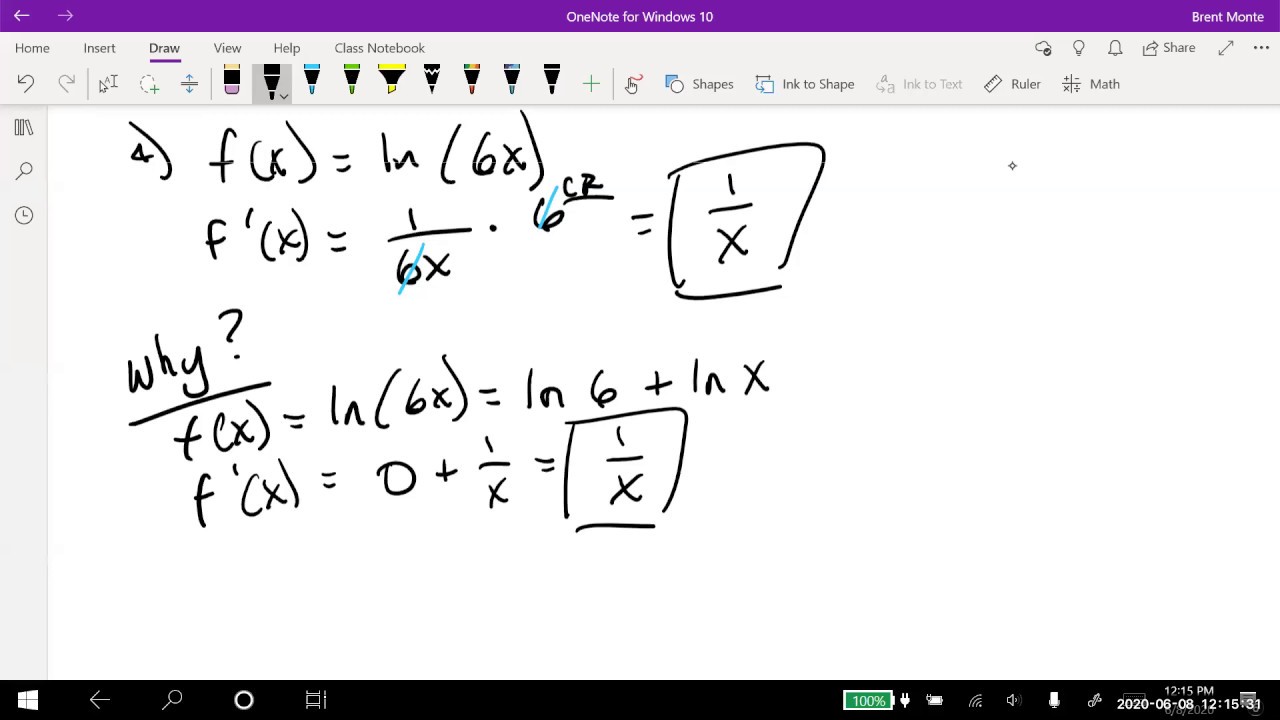
In the example provided, how is the derivative of y = ln(x^2 + x) found?
-The derivative is found by applying the rule (1/(x^2 + x)) and then multiplying by the derivative of the inside (2x + 1), resulting in (2x + 1)/(x^2 + x).
How do you rewrite the cube root of log base 7 of x to use the chain rule for derivatives?
-You rewrite the cube root of log base 7 of x as (log base 7 of x)^(1/3) and then apply the chain rule, resulting in (1/3) * (log base 7 of x)^(-2/3) * (1/x * ln(7)).
What property of logarithms allows you to simplify the derivative of ln(x^4 * sin(x))?
-The property that allows simplification is the ability to break up multiplication inside a logarithm into addition. So, ln(x^4 * sin(x)) can be rewritten as ln(x^4) + ln(sin(x)), which simplifies to ln(x) + ln(sin(x)) after using the exponent rule to pull out constants.
How is the derivative of ln(x^4 * sin(x)) simplified using the properties of logarithms?
-By using the properties of logarithms to rewrite ln(x^4 * sin(x)) as ln(x^4) + ln(sin(x)), and then applying the chain rule, the derivative is simplified to (4/x) + (cos(x)/sin(x)), which can be further simplified to (4/x) + cot(x).
What is the quotient rule used to find the derivative of y = ln(x) / (1 + ln(2x))?
-The quotient rule states that the derivative of a quotient is (bottom * derivative of top - top * derivative of bottom) / (bottom squared). For y = ln(x) / (1 + ln(2x)), the derivative is found by applying this rule, resulting in ((1 + ln(2x)) * (1/x) - ln(x) * (1/(2x) * 2)) / (1 + ln(2x))^2.
What is the final simplified form of the derivative of y = ln(x) / (1 + ln(2x))?
-After applying the quotient rule and simplifying, the derivative is (1 + ln(2x) - ln(x)) / (x * (1 + ln(2x))^2), which can be further simplified by factoring out common terms.
Outlines
📚 Introduction to Derivatives of Logarithmic Functions
The video begins with an introduction to the derivatives of logarithmic functions, focusing on the natural logarithm (Ln). The presenter explains that the derivative of f(x) = Ln(x) is simply 1/x. The video then delves into more complex scenarios, such as the derivative of Ln(g(x)), where g(x) is a more complicated function. Here, the chain rule is applied, multiplying 1/(g(x)) by the derivative of g(x). The video also covers the derivative of a logarithm with a base other than e (the natural logarithm base), which is given as 1/x multiplied by the natural logarithm of the base. Finally, the video discusses the derivative of a generic logarithm, log_a(g(x)), which follows a similar pattern but includes the natural logarithm of the base 'a'. The presenter emphasizes that knowing these formulas is crucial for understanding the derivatives of logarithmic functions and that regular differentiation rules such as the quotient rule, product rule, and chain rule are still applicable.
🧮 Derivative Examples and Logarithmic Properties
The video continues with several examples to illustrate the application of the previously discussed formulas. The first example involves the derivative of y = a natural logarithm of (x^2 + x), which is solved using the chain rule and the derivative of the inside function. The second example is the cube root of log base 7 of X, which is rewritten as a fractional exponent and solved using the chain rule, resulting in an expression involving the natural logarithm of 7. The third example is the natural logarithm of X to the fourth times the sine of X. The presenter demonstrates a simplification technique using logarithmic properties to break down the expression before differentiating, which simplifies the process significantly. The final example is the derivative of y = Ln(X) / (1 + Ln(2X)), which is solved using the quotient rule, and the presenter shows how to simplify the resulting expression. Throughout the examples, the presenter emphasizes the importance of understanding logarithmic properties and applying them to make differentiation easier.
Mindmap
Keywords
💡Derivatives
💡Logarithm Functions
💡Natural Logarithm
💡Chain Rule
💡Quotient Rule
💡Product Rule
💡Logarithmic Base
💡Fractional Exponents
💡Properties of Logarithms
💡Cotangent
💡Differentiation Examples
Highlights
Derivatives of logarithm functions are discussed with two essential formulas to know.
The derivative of f(x) = ln(x) is simply 1/x.
For a more generic function like ln(g(x)), the derivative involves the chain rule and the derivative of g(x).
If the logarithm is not base e, the derivative involves multiplying by the natural logarithm of the base.
A general formula for the derivative of log base a of G(x) is presented, emphasizing the role of the base's natural logarithm.
The importance of knowing the general formulas for taking derivatives of logarithmic functions is emphasized.
The use of regular quotient rule, product rule, and other rules in conjunction with logarithmic derivative formulas is mentioned.
An example is given where y = ln(x^2 + x), demonstrating the application of the derivative rule for logarithmic functions.
The cube root of log base 7 of X is simplified using fractional exponents and the chain rule.
The derivative of log base 7 of X to the 1/3 power involves multiplying by 1/X and the natural logarithm of the base.
An example of ln(X^4 * sin(X)) is used to showcase the simplification of derivatives using logarithmic properties.
The product rule is avoided by rewriting the logarithmic expression as a sum inside the natural logarithm.
The derivative of ln(X/(1 + ln(2X))) is calculated using the quotient rule and simplification techniques.
The cancellation of terms and factoring is used to simplify the derivative expression.
The final simplified form of the derivative of ln(X/(1 + ln(2X))) is expressed as (1 + ln(2X)^2) / (X(1 + ln(2X))) - ln(X).
The video provides several straightforward derivative examples using logarithmic functions.
The presenter offers to answer any further questions and invites viewers to explore more examples on their website.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: