Indefinite integrals: sums & multiples | AP Calculus AB | Khan Academy
TLDRThe video script discusses two fundamental properties of indefinite integrals, emphasizing their importance in calculus. The first property allows the indefinite integral of a sum of functions to be expressed as the sum of their individual integrals. The second property permits the factorization of a constant out of the integral, enabling the constant to be multiplied by the integral of the function. The instructor illustrates these concepts with examples and provides a proof using derivative properties to demonstrate the validity of these properties. Understanding these properties is crucial for solving more complex integrals, as they simplify the process and make it more manageable.
Takeaways
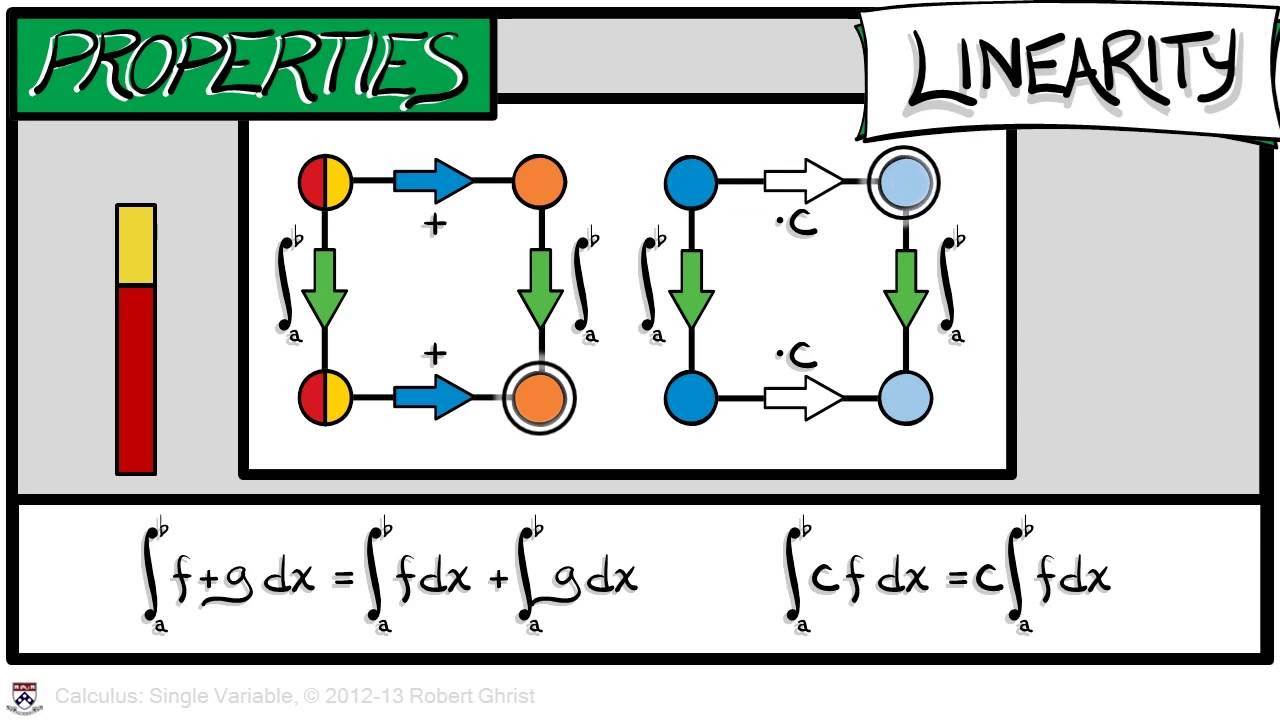
- 📚 The indefinite integral of the sum of two functions is equal to the sum of their individual indefinite integrals.
- 🔢 The indefinite integral of a constant times a function is equal to the constant times the indefinite integral of that function.
- 🔍 These properties are powerful and useful for solving more complex integrals.
- 💡 Understanding these properties can enhance one's ability to tackle more challenging integral problems.
- 📈 The properties can be proven using derivative properties by taking the derivative of both sides of the equation to show equality.
- 🌟 The derivative of the sum of two functions is the sum of their derivatives.
- 📊 When differentiating the indefinite integral of a constant times a function, the constant remains outside the differentiation process.
- 🧩 Breaking down complex integrals into simpler parts allows for easier computation and understanding.
- 🌐 Example: The indefinite integral of x squared plus cosine of x can be separated into the sum of their individual integrals for easier evaluation.
- 📱 For another example, the constant pi in the integral of pi times sine of x can be factored out, simplifying the process.
- 🎯 The key to these properties lies not only in understanding them but also in knowing when and how to apply them in solving integrals.
Q & A
What are the two significant properties of indefinite integrals mentioned in the transcript?
-The two significant properties are: (1) the indefinite integral of the sum of two functions is equal to the sum of the indefinite integrals of each function, and (2) the indefinite integral of a constant times a function is the same as the constant times the indefinite integral of that function.
How can the property of indefinite integrals be useful in solving more complex integrals?
-These properties can simplify the process of finding the indefinite integral of complex functions by breaking them down into simpler parts. For example, the integral of a sum of functions can be found by integrating each function separately and then adding the results. Similarly, a constant factor can be factored out and then multiplied back into the result of the integral.
What happens when we take the derivative of an indefinite integral with respect to x?
-When we take the derivative of an indefinite integral with respect to x, we get the original function that was integrated, according to the fundamental theorem of calculus. This is because the process of integration and differentiation are inverse operations.
Why is the constant of integration added in indefinite integrals?
-The constant of integration is added to account for the fact that differentiation produces a zero for constants, meaning that an original function could have had a constant term that does not affect its derivative. The constant of integration represents the arbitrary constant that could have been part of the original function.
How does the property of indefinite integrals relate to the derivative properties?
-The properties of indefinite integrals are derived from and are consistent with the properties of derivatives. For instance, the linearity of derivatives allows us to factor out constants and sum derivatives, which in turn corresponds to the ability to factor out constants and sum integrals in the indefinite integral properties.
What is the role of the fundamental theorem of calculus in the properties discussed?
-The fundamental theorem of calculus connects the process of differentiation and integration. It states that if a function is continuous on an interval, then the definite integral of the function over that interval can be found by evaluating the antiderivative at the endpoints of the interval and taking the difference. This theorem underpins the ability to break down and reassemble integrals as discussed in the properties.
How can we verify the properties of indefinite integrals?
-We can verify the properties of indefinite integrals by taking the derivative of both sides of the equations representing the properties and showing that the resulting expressions are equal. This process uses the reverse operation (differentiation) to confirm the validity of the integration process.
What is the practical application of taking a constant out of an integral?
-Taking a constant out of an integral simplifies the process of integration. It allows us to treat the constant as a separate factor, which can then be multiplied by the result of the integral of the remaining function. This can make the calculation easier and quicker, especially when dealing with constants that are complex or involve functions themselves.
Can you provide an example of how the properties of indefinite integrals can simplify the integration process?
-Sure, consider the indefinite integral of the function 3x^2 + 2x + 5. Using the properties of indefinite integrals, we can break this down into the sum of three separate integrals: ∫(3x^2)dx + ∫(2x)dx + ∫(5)dx. Each of these integrals can be calculated individually, and then we simply add the results to find the overall antiderivative.
What is the significance of the linearity property of indefinite integrals in calculus?
-The linearity property of indefinite integrals is significant because it allows us to break down complex integration problems into simpler, manageable parts. This property is particularly useful when dealing with sums or differences of functions or when a function is multiplied by a constant, as it enables us to handle each part of the expression separately and then combine the results, often simplifying the overall integration process.
How does the process of integration help us understand the relationship between functions and their derivatives?
-Integration is essentially the reverse process of differentiation. By understanding how a function's derivative can be integrated to find the original function (or one of its antiderivatives), we gain insight into how functions change and evolve. This relationship is fundamental to calculus and is used to solve a wide range of mathematical and real-world problems.
Outlines
📚 Properties of Indefinite Integrals
This paragraph introduces two key properties of indefinite integrals that are crucial for understanding calculus. The first property is that the indefinite integral of the sum of two functions is equal to the sum of the indefinite integrals of each function separately. This means that integration can be broken down into simpler parts, making complex integrals more manageable. The second property discussed is that the indefinite integral of a constant times a function is equal to the constant times the indefinite integral of that function. This allows for constants to be factored out of the integral, simplifying the process. The instructor also suggests that while these properties can be accepted as written, a deeper understanding can be achieved by examining their derivations. This involves taking the derivative of both sides of the equations to demonstrate that the properties hold true after the integrals are eliminated. The paragraph emphasizes the practicality of these properties in solving real-world integral problems, such as integrating a sum of functions or dealing with constants in the integrand. It concludes by encouraging the application of these properties in future calculus problems, thereby reinforcing their utility and importance.
Mindmap
Keywords
💡indefinite integral
💡sum of functions
💡constant
💡derivative properties
💡taking the derivative
💡equality
💡integral of a sum
💡constant times a function
💡proof
💡integration
💡x squared plus cosine of x
Highlights
Indefinite integrals have two significant properties that are very powerful.
The indefinite integral of the sum of two functions is equal to the sum of the indefinite integrals of each function.
The indefinite integral of a constant times a function is equal to the constant times the indefinite integral of that function.
These properties are useful for simplifying complex integrals by breaking them down into simpler parts.
The properties can be proven using derivative properties, by taking the derivative of both sides to show equality.
When differentiating the sum of two indefinite integrals, the result is the function inside the integral.
The derivative of the sum of two functions is the sum of their derivatives, which applies to the indefinite integrals as well.
For the constant times a function property, the left-hand side becomes the constant times the function when differentiated.
The right-hand side of the constant times a function property simplifies to the constant times the integral of the function.
The derivative of a constant times a function simplifies to the constant times the derivative of the function, which is key to proving the property.
These properties are not only true but also important to know when to apply them in solving integrals.
An example of applying the properties is the integral of x squared plus cosine of x, which can be broken down into separate integrals.
The integral of pi times sine of x can be simplified by taking the constant pi out of the integral, showcasing the practical use of these properties.
Understanding these properties is crucial for solving more complex integrals and can greatly simplify the process.
These properties are foundational for advanced calculus and integral calculus techniques.
The proof using derivatives reinforces the validity of these indefinite integral properties and builds confidence in their application.
Transcripts
Browse More Related Video

Breaking up integral interval | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
Calculus Chapter 3 Lecture 25 Definite Integrals

Math 1325 Lecture 13 2

Calculus 1 Lecture 4.5: The Fundamental Theorem of Calculus
Another u-subsitution example

Lec 19 | MIT 18.01 Single Variable Calculus, Fall 2007
5.0 / 5 (0 votes)
Thanks for rating: