The Chain Rule

Khan Academy

3 Oct 200709:12

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, the presenter reviews the concept of derivatives and introduces the chain rule, a powerful tool for differentiating complex functions. By walking through examples, the video explains how to apply the chain rule to break down and simplify the process of finding derivatives, emphasizing its practical applications in solving real-world problems. The presenter's approach focuses on clarity and understanding through examples, promising a more formal definition in a subsequent video.

Takeaways

📚 The concept of derivatives is being reviewed and expanded upon.
🔄 Introduction of the chain rule for taking derivatives of more complex functions.
🌟 Derivatives can be computed by taking derivatives of individual components and then combining them.
📈 Example given: f(x) = 10x^7 + 6x^3 + 15x - x^16, and its derivative is found by applying derivatives to each term.
🎢 Understanding the slope of a curve at any point x is the main application of finding f'(x), the derivative function.
🖌️ Derivative function is used to find the slope of the tangent line at any point on a curve.
🌈 Chain rule simplifies the process of finding derivatives of functions that are not simple polynomials.
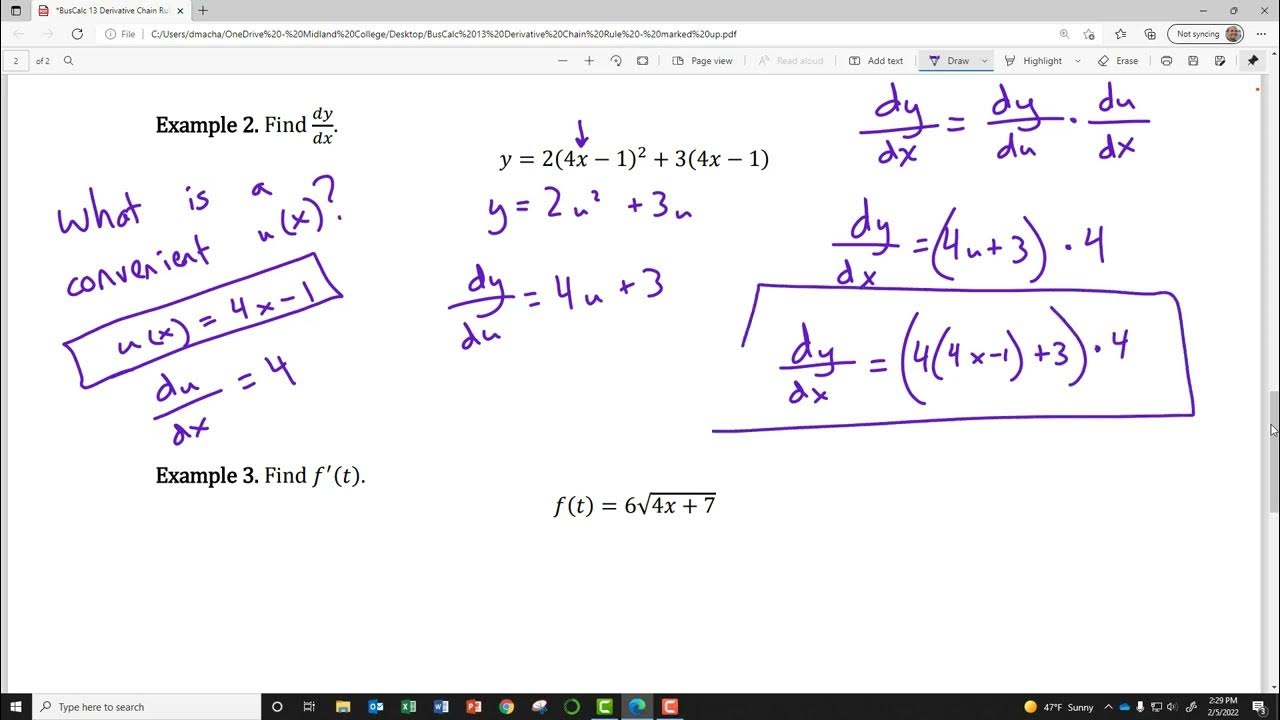
🔢 Example using chain rule: (2x + 3)^5, the derivative is found by treating (2x + 3) as a single variable and applying the chain rule.
📊 Another example: g(x) = x^2 + 2x + 3^8, its derivative is calculated using the chain rule by considering the inner function and the outer function separately.
📚 More examples and a formal definition of the chain rule will be provided in subsequent presentations.

Q & A

What is the main topic of the video script?
-The main topic of the video script is the concept of derivatives in calculus, with a focus on reviewing basic derivatives and introducing the chain rule for more complex functions.
How does the script illustrate the process of taking a derivative of a function?
-The script illustrates the process by first reviewing the method of taking derivatives of individual terms of a polynomial function and then introducing the chain rule for more complex functions, which involves taking the derivative of subfunctions and multiplying by the derivative of the entire function.
What is the chain rule?
-The chain rule is a method in calculus for finding the derivative of a composite function. It allows you to take the derivative of a function by taking the derivative of its subfunctions and then multiplying by the derivative of the entire function.
How does the script demonstrate the chain rule?
-The script demonstrates the chain rule by walking through examples of functions that are not simple polynomials. It shows how to take the derivative of the inner function, multiply by the derivative of the outer function, and then simplify the result.
What is the purpose of the derivative function?
-The purpose of the derivative function is to determine the slope of the tangent line at any point along a curve. It provides information about the rate of change or the steepness of the function at a specific point.
What is the derivative of f(x) = 10x^7 + 6x^3 - 15x^(-16)?
-The derivative of f(x) = 10x^7 + 6x^3 - 15x^(-16) is f'(x) = 70x^6 - 48x^(-15) + 15 - 16x^(-15).
How does the script suggest learning the chain rule?
-The script suggests learning the chain rule through examples rather than starting with a formal definition. It emphasizes understanding the concept through practical application and repetition.
What is the derivative of g(x) = (x^2 + 2x + 3)^8?
-The derivative of g(x) = (x^2 + 2x + 3)^8 is g'(x) = 8(x^2 + 2x + 3)^7 * (2x + 2).
Why is the chain rule useful in calculus?
-The chain rule is useful because it simplifies the process of finding derivatives for complex functions, especially composite functions, without the need to expand and differentiate each term individually.
What does the script imply about the teaching approach for the chain rule?
-The script implies that a hands-on, example-based approach is more effective for understanding the chain rule than starting with a formal definition. It suggests that practical application and repetition will lead to a better grasp of the concept.
How does the script address the challenge of erasing on a digital chalkboard?
-The script humorously acknowledges the challenge of erasing on a digital chalkboard and resorts to 'the old-fashioned way' of erasing, which is a nod to the traditional teaching methods while using modern tools.

Outlines

00:00

📚 Introduction to Derivatives and the Chain Rule

This paragraph introduces the concept of derivatives and sets the stage for a deeper exploration of the chain rule. The speaker begins by reviewing previous lessons on derivatives, emphasizing the importance of understanding how to calculate the slope of a curve at any given point. The explanation includes a practical demonstration of how to find the derivative of a polynomial function, using a specific example to illustrate the process. The speaker then transitions into discussing the chain rule, a powerful tool that expands the range of functions for which derivatives can be calculated. The paragraph concludes with a promise to delve further into the chain rule and its applications in future presentations, highlighting the utility of derivatives in solving a variety of mathematical problems.

05:01

🔍 Applying the Chain Rule to Derivatives

In this paragraph, the focus shifts to applying the chain rule to calculate derivatives of more complex functions. The speaker explains that the chain rule allows for the differentiation of composite functions by breaking them down into simpler subfunctions. The explanation is supported by a step-by-step walkthrough of how to use the chain rule, using a specific function as an example. The speaker also emphasizes the practicality of the chain rule, as it simplifies the process of differentiation compared to expanding and simplifying complex functions. The paragraph ends with a commitment to provide more examples and a formal definition of the chain rule in subsequent presentations, aiming to solidify the understanding of this fundamental calculus concept.

Mindmap

Keywords

💡derivatives

Derivatives are a fundamental concept in calculus that represent the rate of change or the slope of a function at any given point. In the context of the video, the focus is on teaching how to calculate the derivatives of various functions, which is essential for understanding the behavior of the functions and their tangent lines at different points.

💡chain rule

The chain rule is a powerful tool in calculus that simplifies the process of finding the derivative of composite functions. It allows us to break down complex functions into simpler parts, take the derivatives of these parts, and then combine them to find the derivative of the entire function. This rule is particularly useful when dealing with functions that are made up of multiple functions nested within each other.

💡slope

Slope is a measure of the steepness of a line, and in the context of the video, it refers to the slope of the tangent line to a curve at a specific point. The derivative of a function at a given point provides this slope, which is a key concept in understanding the behavior of the function at that point, including how fast it is increasing or decreasing.

💡polynomial functions

Polynomial functions are mathematical functions that involve only the variables and whole number exponents, and can include addition, subtraction, multiplication, and non-negative integer exponents of the variable. In the video, the讲师 demonstrates how to find the derivatives of polynomial functions by taking the derivatives of each term individually and then adding them together.

💡composite functions

Composite functions are functions that are made up of two or more functions combined in such a way that the output of one function becomes the input of the next. The chain rule is particularly useful for differentiating composite functions, as it allows us to break down the process into simpler steps and apply the derivatives of each individual function.

💡tangent line

A tangent line is a line that touches a curve at a single point without crossing it. The slope of the tangent line at any given point on a curve is equal to the derivative of the function representing the curve at that point. Tangent lines are important in calculus as they provide information about the local behavior of a function, including the rate of change and direction of increase or decrease.

💡rate of change

The rate of change is a measure of how quickly a quantity changes with respect to another quantity. In calculus, the rate of change is often represented by derivatives and is used to analyze the behavior of functions, particularly how they change over intervals of the independent variable.

💡exponential functions

Exponential functions are a class of functions where the variable appears in the exponent. They have distinctive growth or decay patterns and are different from polynomial functions. The video touches on the concept of differentiating such functions, specifically when they are part of composite functions.

💡differentiation

Differentiation is the process of finding the derivative of a function, which gives us information about the function's behavior, such as its rate of change and the slope of its tangent lines. It is one of the main operations in calculus and is crucial for solving a wide range of mathematical problems involving change.

💡function composition

Function composition occurs when one function is applied after another, resulting in a new function. In the context of the video, understanding function composition is important for applying the chain rule, as it involves taking the derivative of the outer function and then applying it to the derivative of the inner function.

Highlights

Introduction to the concept of derivatives and their application in understanding the slope of a curve at any given point.

Review of the process of taking derivatives of a polynomial function, emphasizing the straightforward nature of the process.

Explanation of how to calculate the derivative of a complex function by breaking it down into parts and using the sum of derivatives.

Illustration of the derivative as a function that provides the slope of the tangent line at any point on the curve, offering geometrical insight into the concept.

Introduction of the chain rule as a powerful tool for calculating derivatives of more complicated functions without the need for extensive multiplication.

Demonstration of the chain rule through examples, showing how to take derivatives of functions that involve both multiplication and exponentiation.

Use of color to differentiate between parts of the function and their derivatives, aiding in understanding the process of the chain rule.

Explanation of treating a subfunction as a variable when applying the chain rule, simplifying the process of finding derivatives.

Presentation of a method for calculating derivatives that avoids the cumbersome task of expanding complex functions.

Emphasis on the practical applications of derivatives, promising to cover a range of word problems and analytical solutions in future presentations.

Acknowledgment of the potential confusion surrounding the chain rule and the intention to clarify it through numerous examples.

Commitment to provide a formal definition of the chain rule after illustrating it with multiple examples, catering to learners who benefit from both conceptual and formal understanding.

Preview of the next presentation, which will focus on a variety of examples using the chain rule to solidify the concept.

The transcript's value lies in its ability to simplify complex mathematical concepts, making them accessible and understandable through practical examples and visual aids.

The unique approach of combining theoretical explanation with visual demonstration and practical application makes the content engaging and effective for learners.

Transcripts

Browse More Related Video

Calculus 3: The Chain Rule (Video #15) | Math with Professor V

BusCalc 13 Derivative Chain Rule

Product rule | Taking derivatives | Differential Calculus | Khan Academy

Math 1325 Lecture 9 6 Chain & Power Rule

Multivariable Chain Rule (Calculus 3)

Calculus 1 Lecture 2.6: Discussion of the Chain Rule for Derivatives of Functions

The Chain Rule

Takeaways

Q & A

What is the main topic of the video script?

How does the script illustrate the process of taking a derivative of a function?

What is the chain rule?

How does the script demonstrate the chain rule?

What is the purpose of the derivative function?

What is the derivative of f(x) = 10x^7 + 6x^3 - 15x^(-16)?

How does the script suggest learning the chain rule?

What is the derivative of g(x) = (x^2 + 2x + 3)^8?

Why is the chain rule useful in calculus?

What does the script imply about the teaching approach for the chain rule?

How does the script address the challenge of erasing on a digital chalkboard?