Calculus 3: The Chain Rule (Video #15) | Math with Professor V

Math with Professor V

17 Jun 202042:19

EducationalLearning

32 Likes 10 Comments

TLDRThis calculus lecture delves into the intricacies of the chain rule, essential for differentiating compositions of functions. The instructor illustrates the rule's application with examples, including differentiating a function involving a square root and a quadratic expression. The video progresses to more complex scenarios, such as functions of several variables, emphasizing the importance of understanding the chain rule's formal statement for these cases. The lecture also introduces tree diagrams to visualize the chain rule process and concludes with practical applications, such as implicit differentiation and related rates problems, showcasing the rule's versatility in solving real-world calculus challenges.

Takeaways

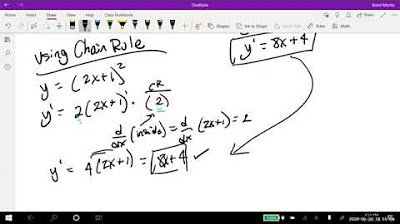
📚 The Chain Rule is essential for differentiating compositions of functions, especially when dealing with functions of a single variable like f(x) = √(3x^2 + 4).
🔍 When applying the Chain Rule, start by differentiating the outer function first, then multiply by the derivative of the inner function, as demonstrated with the example of f(x).
📉 For functions of several variables, the Chain Rule can take multiple forms depending on whether the inner function is a function of one or several variables.
🌐 Understanding the formal statement of the Chain Rule is crucial, especially when dealing with functions like Y(U(G(x))) where Y is a function of U, and U is a function of X.
📝 It's important to use the correct notation for derivatives, such as 'D' for total derivatives and 'del' for partial derivatives, especially in multivariable calculus.
📈 Tree diagrams can be a helpful tool for visualizing the Chain Rule process, especially for complex functions with multiple variables.
🔧 The Chain Rule can be used to solve implicit differentiation problems by differentiating both sides of an equation with respect to a variable and isolating dy/dx.
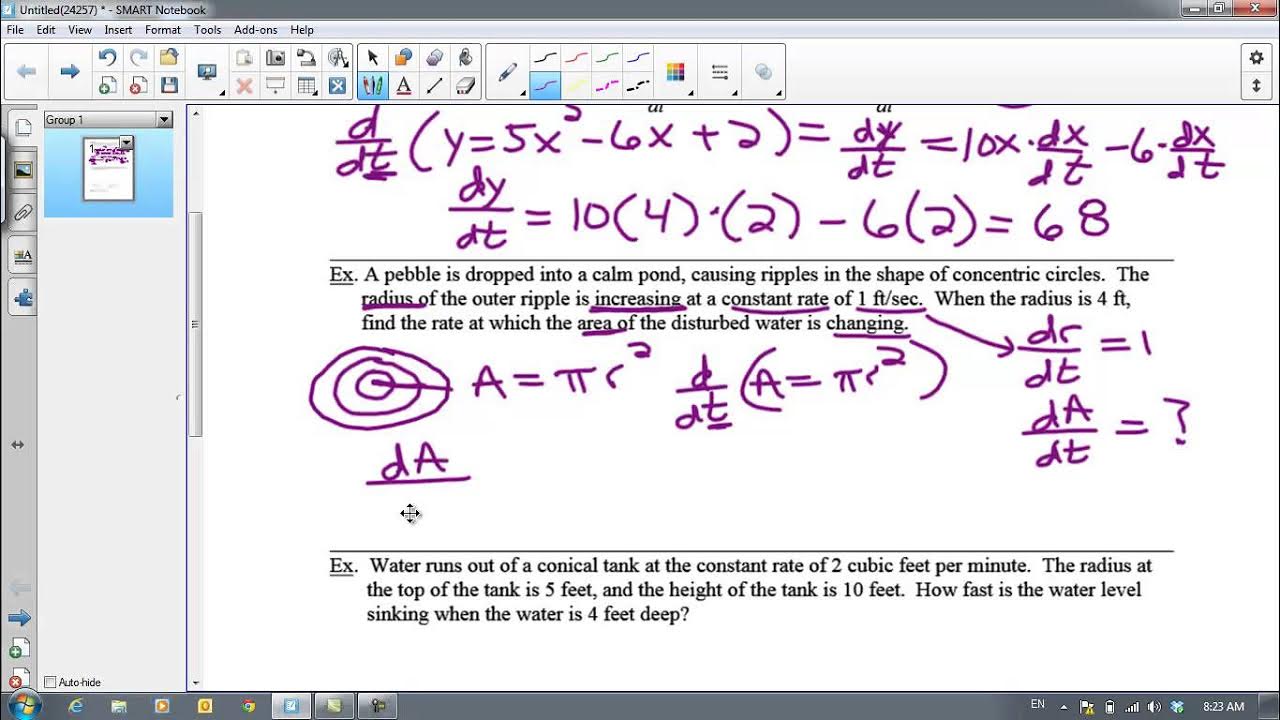
💧 Related rates problems, such as finding the rate at which the water level is rising in a cone-shaped tank, can be tackled using the Chain Rule by relating the variables with a given formula and differentiating.
📐 For related rates involving geometric shapes, it's often necessary to rewrite the volume or area formula in terms of a single variable to simplify the differentiation process.
🔑 The Chain Rule is not only limited to basic calculus but extends to more advanced topics, including directional derivatives and the gradient vector, which are covered in subsequent lessons.

Q & A

What is the chain rule used for in calculus?
-The chain rule is used for differentiating a composition of functions, where you have a function of another function.
Can you provide an example of using the chain rule with a function of one variable?
-Sure, if you have a function f(x) = √(3x^2 + 4), you would first differentiate the outer function (√x) and then multiply by the derivative of the inner function (3x^2 + 4), resulting in f'(x) = (3x)/(2√(3x^2 + 4)).
What is the formal statement of the chain rule for functions of several variables?
-If y is a function of u, and u is a function of x, with both being differentiable, then dy/dx = (dy/du) * (du/dx).
How does the chain rule change when dealing with functions of several variables?
-The chain rule can take on different forms depending on whether the inner function is a function of one or several variables. It involves taking successive derivatives as you work your way inside the composition.
What is a tree diagram in the context of the chain rule for functions of several variables?
-A tree diagram is a visual tool to help organize and understand the chain rule for functions of several variables. It starts with the outer function and branches out to each variable, showing the path of differentiation from the outer function to the inner variables.
Why is it important to use the correct notation when applying the chain rule to functions of several variables?
-Using the correct notation, such as 'D' for total derivatives and 'del' for partial derivatives, ensures clarity and accuracy in expressing the chain rule and helps avoid confusion about the order of differentiation.
Can you explain how to find the derivative of a function of several variables using the chain rule?
-Yes, if you have a function Z = f(x, y) and both x and y are functions of t, then dZ/dt = (∂Z/∂x) * (dx/dt) + (∂Z/∂y) * (dy/dt), where ∂Z/∂x and ∂Z/∂y are partial derivatives.
What is the purpose of the chain rule in implicit differentiation?
-The chain rule in implicit differentiation allows you to find the derivative of an implicitly defined function by differentiating both sides of the equation with respect to the variable of interest, isolating the desired derivative.
How can the chain rule be used to solve related rates problems?
-In related rates problems, the chain rule helps relate the rates of change of different quantities by differentiating an equation that connects these quantities with respect to time, allowing you to find an unknown rate of change.
Can you give an example of a related rates problem involving a cone?
-Certainly, if you have a cone with a base radius that is always half the height, and water is being pumped into the tank at a rate of 2 cubic meters per minute, you can use the chain rule to find the rate at which the water level is rising when the water is 3 meters deep.
What is the significance of rewriting the volume function of a cone in terms of a single variable?
-Rewriting the volume function in terms of a single variable simplifies the differentiation process and allows you to relate different variables, such as the radius and height of the cone, which can be crucial for solving related rates problems.

Outlines

00:00

📚 Introduction to the Chain Rule in Calculus

This paragraph introduces the concept of the chain rule in calculus, which is essential for differentiating compositions of functions. The lecturer uses a specific example where the function f(x) is the square root of (3x^2 + 4). The process of differentiating this function step by step is explained, starting with differentiating the outer function and then applying the chain rule to multiply by the derivative of the inner function. The formal statement of the chain rule for functions of a single variable and then for functions of several variables is discussed, with an emphasis on understanding rather than memorization. The paragraph also introduces the idea of using a tree diagram to visualize the chain rule process.

05:01

🌐 Chain Rule for Functions of Several Variables

The paragraph delves deeper into the chain rule, particularly for functions of several variables. It presents different cases where the inner function u might be a function of one or several variables, emphasizing the need to understand how to set up chain rule problems rather than memorizing specific formulas. A formal proof for one case of the chain rule is provided, involving limits and differentials, to show how the chain rule is derived. The importance of using the correct notation for total derivatives (D) and partial derivatives (del) is highlighted, and a tree diagram is used to illustrate the process of differentiating a function of two variables with respect to a single variable.

10:03

🔍 Applying the Chain Rule to Implicit Differentiation

This section discusses the application of the chain rule to implicit differentiation, starting with a review of implicit differentiation for functions of a single variable. The process involves differentiating both sides of an equation term by term and isolating dy/dx. The paragraph then extends this concept to functions of several variables, showing how to use the chain rule to find partial derivatives when an equation defines a variable implicitly. An example is provided where a function of x and y is set to zero, and the chain rule is used to solve for dy/dx by taking partial derivatives with respect to x and y.

15:05

📘 Advanced Chain Rule Applications and Related Rates

The paragraph explores advanced applications of the chain rule, including its use in related rates problems. It presents a scenario involving a water tank in the shape of a circular cone, where water is being pumped in at a certain rate, and the task is to find the rate at which the water level is rising. The solution involves rewriting the volume formula of the cone in terms of a single variable, due to the relationship between the radius and height of the cone, and then differentiating with respect to time using the chain rule. The paragraph concludes with a more complex related rates problem involving a cone where both the radius and height are changing with time.

20:17

📊 Solving Related Rates Problems with Partial Derivatives

This paragraph focuses on solving related rates problems using partial derivatives. It presents a step-by-step approach to finding the rate of change of the volume of a cone when the radius and height are changing at given rates. The solution involves taking partial derivatives of the volume formula with respect to both the radius and height, and then using the given rates of change to find the rate of change of the volume. The paragraph also emphasizes the importance of understanding the relationships between variables in related rates problems and how to differentiate equations accordingly.

25:17

🎓 Conclusion and Upcoming Topics

The final paragraph wraps up the lesson on the chain rule and its applications, highlighting the importance of understanding the chain rule for functions of several variables and its use in solving related rates problems. It also teases upcoming topics, such as directional derivatives and the gradient vector, indicating a continuation of the mathematical concepts being explored in the calculus course.

Mindmap

Keywords

💡Chain Rule

The chain rule is a fundamental principle in calculus for differentiating composite functions. It states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function. In the video, the chain rule is applied to various examples, such as differentiating a function that involves a square root of a quadratic expression, illustrating its application in simplifying complex derivative calculations.

💡Derivative

A derivative in calculus represents the rate at which a function changes with respect to its variable. It is a fundamental concept used to analyze the behavior of functions, including finding slopes of tangent lines and determining rates of change. The video script discusses finding derivatives of various functions, emphasizing the process of differentiation as a means to understand how one quantity changes in relation to another.

💡Partial Derivative

A partial derivative is the derivative of a function with respect to one variable, while treating other variables as constants. It is used in multivariable calculus to understand how a function changes with respect to one dimension while holding others constant. The script explains how to compute partial derivatives in the context of functions of several variables, such as when dealing with rates of change in different dimensions of a geometric shape.

💡Differentiation

Differentiation is the process of finding the derivative of a function. It is a key operation in calculus that allows for the analysis of a function's behavior, including finding maximum and minimum values, slopes, and understanding rates of change. The video lecture focuses on differentiation techniques, particularly the chain rule, to find derivatives of complex functions.

💡Composite Function

A composite function is created by using one function as the input to another function. For example, if f(x) and g(x) are functions, then the composite function would be f(g(x)). The chain rule is essential when differentiating composite functions because it breaks down the process into manageable steps by differentiating the outer function first and then the inner function. The script provides an example of differentiating a composite function involving a square root and a quadratic expression.

💡Variable

In calculus, a variable represents a quantity that can change or take on different values. The script discusses functions of one variable and several variables, emphasizing the importance of understanding how functions change with respect to their variables. Variables are central to the concept of differentiation, as they allow for the exploration of how one quantity affects another.

💡Function of Several Variables

A function of several variables is a mathematical function that depends on multiple inputs. For instance, a function f(x, y, z) depends on three variables. The script explains how to apply the chain rule to functions of several variables, which can become more complex due to the interplay between the variables. Understanding these functions is crucial for solving problems in multivariable calculus.

💡Implicit Differentiation

Implicit differentiation is a technique used when a function is defined implicitly, meaning the variable of interest is not isolated on one side of the equation. This method involves differentiating both sides of an equation with respect to a variable, treating all other variables as if they were functions of that variable. The script demonstrates implicit differentiation in the context of solving for dy/dx in an equation involving both x and y.

💡Related Rates

Related rates problems involve finding the rate of change of one quantity given the rate of change of another related quantity. These problems often arise in real-world scenarios, such as physics or engineering, where multiple quantities are interdependent. The script discusses related rates in the context of a water tank problem, where the rate of change of volume and radius are known, and the rate of change of height is sought.

💡Volume

Volume is a measure of the amount of space occupied by a three-dimensional object. In the context of the video, the volume of a cone is calculated using the formula V = (1/3)πr²h, where r is the radius and h is the height. The script uses this formula to explore how the volume of a cone changes with respect to time as its dimensions change, demonstrating the application of calculus in geometry.

Highlights

Introduction to the chain rule for differentiating compositions of functions.

Example given to demonstrate the process of differentiating a function using the chain rule.

Differentiation of the outer function first, followed by the inner function as per the chain rule.

Explanation of the formal statement of the chain rule for functions of several variables.

Different forms of the chain rule based on the number of variables the inner function depends on.

Case 1 of the chain rule for functions of two variables, each being a function of a single variable.

Emphasis on the correct use of total derivatives (D) and partial derivatives (del).

Instruction to write out the chain rule before computation for clarity and credit in exams.

Introduction of tree diagrams as a tool for visualizing the chain rule process.

Proof of the chain rule for the case of a function of two variables, each depending on a single variable.

Application of the chain rule to find the derivative of a function involving exponential and trigonometric functions.

Case 2 of the chain rule for functions of two variables, each now being functions of two variables.

Use of tree diagrams to formulate the chain rule for functions of multiple variables.

Implicit differentiation using the chain rule for functions of a single variable.

Generalization of implicit differentiation to functions of several variables using partial derivatives.

Application of the chain rule to related rates problems in calculus, such as the water tank problem.

Solution to a related rates problem involving the volume of a cone with changing dimensions.

Conclusion summarizing the versatility of the chain rule in calculus.

Transcripts

Browse More Related Video

Unit II: Lec 3 | MIT Calculus Revisited: Single Variable Calculus

Math 1325 Lecture 9 6 Chain & Power Rule

Chain Rule For Finding Derivatives

Related Rates

Related Rates Day 1

Math 11 - Sections 1.7-1.8

Related Tags

Chain Rule Calculus Differentiation Multivariable Partial Derivatives Implicit Differentiation Related Rates Volume Cones Educational Content Math Tutorial Lecture Script