_-substitution: multiplying by a constant | AP Calculus AB | Khan Academy

Khan Academy
28 Dec 201205:32
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a step-by-step guide on how to apply u-substitution to compute the indefinite integral of the square root of 7x plus 9 with respect to dx. Initially, it seems that u-substitution may not be directly applicable, but by multiplying the integral by 1/7, the derivative of the u-substitute (7) becomes visible. The video demonstrates the process of rewriting the integral in terms of u, applying the reverse power rule, and eventually substituting back to the original variable to obtain the final result, which is 2/21 times (7x plus 9) to the 3/2 power plus a constant, showcasing the power of creative manipulation and scalar properties in integral calculus.

Takeaways
  • 📚 The indefinite integral of √(7x+9) dx can be approached using u-substitution.
  • 🤔 Initially, the derivative of the integrand (7) is not immediately visible, prompting a closer look at the integral expression.
  • 🔄 By multiplying and dividing the integral by 7, scalar properties are used to reveal the derivative within the integral.
  • 👉 The integral is rewritten as 1/7 * ∫(√(7x+9) * 7) dx, allowing for u to be defined as 7x + 9.
  • 🎓 The derivative of u with respect to x (du = 7dx) is identified, streamlining the u-substitution process.
  • 📈 After substitution, the integral simplifies to 1/7 * ∫u^(1/2) du, focusing on the antiderivative of the transformed function.
  • 🔢 The antiderivative is found by increasing the power of u by one, resulting in u^(3/2), and applying the reverse power rule.
  • 📊 The final antiderivative is expressed as 2/21 * u^(3/2) + C, incorporating the constant of integration and the original scalar multiplier.
  • 🔄 The expression is then unsubstituted back to its original variables, replacing u with 7x + 9.
  • 🎉 The result is a simplified integral: 2/21 * (7x + 9)^(3/2) + C, showcasing the successful application of u-substitution.
Q & A

  • What is the integral being evaluated in the script?

    -The integral being evaluated is the indefinite integral of the square root of 7x plus 9 with respect to dx.

  • Why might u-substitution initially seem inapplicable for this integral?

    -U-substitution might initially seem inapplicable because the derivative of the function set to u (7x + 9) does not directly appear in the integral.

  • How does the video suggest modifying the integral to make u-substitution applicable?

    -The video suggests multiplying the integral by 1/7 to make the coefficient of the square root term equal to 7, which is the derivative of the proposed u value (7x + 9).

  • What is the value of u used in the u-substitution?

    -The value of u used in the u-substitution is 7x plus 9.

  • What is the derivative of u with respect to x after the modification?

    -After the modification, the derivative of u with respect to x is 7, as u is equal to 7x plus 9.

  • What is the antiderivative of u to the 1/2 power?

    -The antiderivative of u to the 1/2 power is u to the 3/2 power, multiplied by the reciprocal of the exponent increment, which is 2/3.

  • How is the constant of integration represented in the final answer?

    -The constant of integration is represented as 'c' in the final answer.

  • What is the final result of the indefinite integral after u-substitution and simplification?

    -The final result of the indefinite integral is 2/21 times (7x plus 9) to the 3/2 power, plus a constant.

  • How does the video emphasize the flexibility of scalars in integrals?

    -The video emphasizes that scalars can be moved in and out of the integral easily, which allows for manipulation of the integral to make u-substitution applicable.

  • What is the purpose of the u-substitution method in this context?

    -The purpose of u-substitution in this context is to simplify the integral and make it easier to evaluate by finding a suitable u such that its derivative is present in the integrand.

  • How does the video demonstrate the reverse power rule?

    -The video demonstrates the reverse power rule by increasing the exponent of u from 1/2 to 3/2 and then multiplying by the reciprocal of the new exponent to find the antiderivative.

Outlines
00:00
📚 Introduction to u-substitution for Indefinite Integral

This paragraph introduces the concept of u-substitution in solving indefinite integrals, specifically focusing on the integral of the square root of 7x plus 9 dx. It begins by questioning whether u-substitution is applicable and suggests setting u to 7x plus 9. The paragraph then discusses the importance of identifying the derivative of u in relation to the integral. It highlights the flexibility of scalar multiplication and division in integrals and demonstrates how to rewrite the integral to make the derivative of u (which is 7) apparent. The process of rewriting the integral in terms of u and applying the reverse power rule is detailed, leading to the identification of the antiderivative in terms of u. Finally, the paragraph emphasizes the need to account for the constant of integration and sets the stage for substituting back in terms of x in the subsequent paragraph.

05:01
🎓 Substituting back to solve the Indefinite Integral

This paragraph concludes the process of solving the indefinite integral using u-substitution. It starts by substituting u back into the expression derived in the previous paragraph, where u is equal to 7x plus 9. The paragraph then simplifies the expression to obtain the final result of the integral, which is 2/21 times 7x plus 9 to the power of 3/2 plus a constant. The explanation underscores the successful application of u-substitution to a complex-looking integral and reassures that, even if not immediately obvious, the method can be effectively applied.

Mindmap
Keywords
💡indefinite integral
The indefinite integral is a fundamental concept in calculus that represents the reverse process of differentiation. It is used to find the original function whose derivative is given. In the context of the video, the indefinite integral of the square root of 7x plus 9 with respect to dx is the main problem to be solved, and the process of finding this integral involves using the u-substitution method.
💡u-substitution
U-substitution is a technique used in calculus to evaluate integrals by changing the variable of integration. It is particularly useful when the integrand is a function of a combination of terms. In the video, u-substitution is suggested as a potential method to evaluate the integral, and the process of setting up the substitution is explained in detail.
💡derivative
A derivative is a concept in calculus that represents the rate of change of a function with respect to its independent variable. In the context of the video, the derivative is used to determine the appropriate substitution variable and to find the differential form of the integral.
💡scalar
In mathematics, a scalar is a quantity that has magnitude but no direction. In the context of the video, scalars are discussed in relation to their ability to be factored in and out of integrals without changing the value of the integral. This property is used to manipulate the integral to make it more suitable for u-substitution.
💡differential form
The differential form of an expression refers to its representation in terms of differentials, such as dx or du, which are infinitesimal changes in the variables. In the video, the differential form of the integral is used to express the relationship between the differentials of u and x, allowing for the application of u-substitution.
💡antiderivative
The antiderivative, also known as the indefinite integral, is a function whose derivative is the given function. It represents the reverse operation of differentiation and is used to find the original function from its derivative. In the video, the antiderivative of u to the 1/2 power is determined to be u to the 3/2 power, which is a key step in solving the integral.
💡power rule
The power rule is a fundamental rule in calculus that describes how to differentiate a function raised to a power. It states that the derivative of a function f(x) raised to the power n is n times f(x) raised to the power (n-1) times the derivative of f(x). In the video, the power rule is used in reverse to find the antiderivative of u to the 1/2 power.
💡constant of integration
The constant of integration, often denoted as 'c', is an arbitrary constant that is added to the antiderivative of a function to account for the infinite number of functions that can have the same derivative. In the video, the constant of integration is included in the final answer to represent this concept.
💡substitute
In the context of the video, substituting refers to the process of replacing one variable or expression with another in the process of solving an integral. This is a key step in the u-substitution method, where the original variable x is replaced by a new variable u.
💡simplify
Simplification in mathematics is the process of making an expression or equation more straightforward or easier to understand. In the video, the goal is to simplify the given integral to a form that can be more easily evaluated using u-substitution.
Highlights

The indefinite integral of the square root of 7x plus 9 dx is discussed.

The possibility of using u-substitution for this integral is considered.

The natural choice for u is 7x plus 9, but its derivative is not immediately visible.

The derivative of u with respect to x is determined to be 7.

The strategy of multiplying and dividing by scalars to make the derivative visible is introduced.

The integral is rewritten by multiplying by 1/7 to make the derivative of u equal to 7.

The integral is expressed in terms of u, specifically as 1/7 times the integral of the square root of u du.

The integral in terms of u is simplified to 1/7 times the integral of u to the 1/2 power du.

The antiderivative of u to the 1/2 power is found to be u to the 3/2 power.

The integral is expressed as 2/21 times u to the 3/2 power plus a constant.

The constant term is included in the integral, maintaining the general form of an antiderivative.

The integral is rewritten with the constant term distributed and simplified.

The substitution of u back into the integral is performed, resulting in the final antiderivative in terms of x.

The final result is 2/21 times (7x plus 9) to the 3/2 power plus a constant, showcasing the successful application of u-substitution.

The process demonstrates the utility of u-substitution even in cases where the derivative of the substitution variable is not immediately apparent.

The method illustrates the importance of recognizing and applying algebraic manipulations to simplify integrals.

Transcripts

Browse More Related Video

_-substitution: rational function | AP Calculus AB | Khan Academy

Fundamental Theorem of Calculus: Changing the Bounds with u-Substitution

_-substitution: definite integrals | AP Calculus AB | Khan Academy

(2^ln x)/x Antiderivative Example

_-substitution intro | AP Calculus AB | Khan Academy

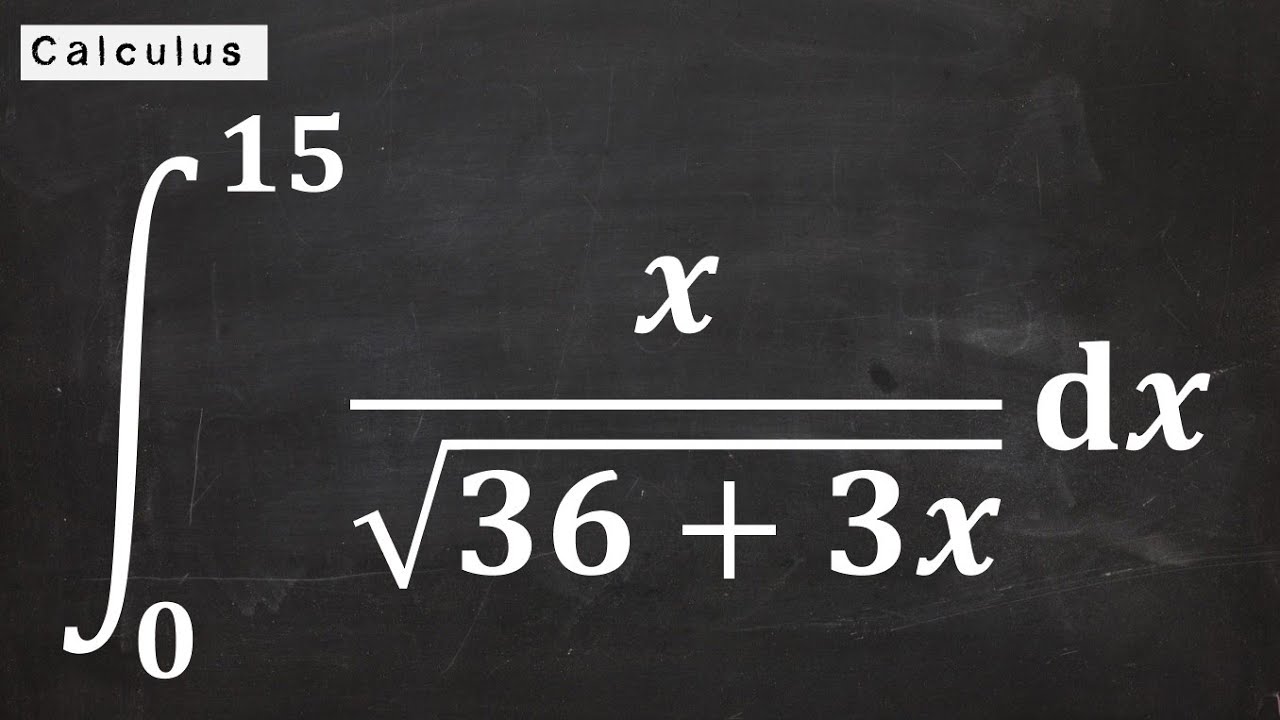
Definite Integral With U-Substitution

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsIntegrationu-SubstitutionComplex AnalysisProblem SolvingEducational ContentMath TutorialCalculus TechniquesMathematics EducationOnline Learning