Definite integral of piecewise function | AP Calculus AB | Khan Academy

Khan Academy
28 Jul 201606:13
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a step-by-step explanation of how to evaluate a piecewise function's definite integral. It introduces the function f(x) and explains the process of splitting the integral into two intervals to handle the piecewise definition. The script then demonstrates the calculation of the integral from -1 to 0 using basic antidifferentiation, resulting in a value of 1/2. Next, it tackles the integral from 0 to 1 by applying u-substitution to the cosine function, ultimately yielding a result of 0. The final answer for the entire definite integral is the sum of both parts, which is 1/2.

Takeaways
  • 📌 The function f(x) is defined piecewise, with f(x) = x + 1 for x < 0 and f(x) = cos(Ï€x) for x ≥ 0.
  • 📈 The definite integral of f(x) from -1 to 1 is evaluated by splitting the integration interval into two parts due to the piecewise definition of the function.
  • 🤔 The first part of the integral, from -1 to 0, uses the antiderivative of x + 1, which is (x^2)/2 + x.
  • 🧮 Evaluating the first part at x = 0 and x = -1 gives a result of 1/2 after applying the limits of integration.
  • 📌 The second part of the integral, from 0 to 1, involves the function cos(Ï€x), which requires a technique like u-substitution to find its antiderivative.
  • 🔄 The substitution u = Ï€x is used, and the derivative of sin(Ï€x) with respect to x is found using the chain rule, resulting in Ï€cos(Ï€x).
  • 🎓 To adjust for the substitution, the integral is multiplied and divided by 1/Ï€, which does not change the value but aligns with the derivative of sin(Ï€x).
  • 📊 The antiderivative of cos(Ï€x) is sin(Ï€x), and the integral is evaluated from 0 to 1, resulting in a final value of 0 because sin(Ï€) - sin(0) = 0.
  • 🔢 Combining the results from both parts of the integral, the total value of the definite integral from -1 to 1 is 1/2.
  • 🌟 The process demonstrates the importance of understanding the piecewise nature of functions and the appropriate techniques to evaluate their definite integrals.
  • 📚 The example serves as a lesson in the application of basic calculus concepts such as antiderivatives, u-substitution, and the evaluation of definite integrals.
Q & A

  • What is the function f(x) defined as for x less than zero?

    -For x less than zero, the function f(x) is defined as x plus one.

  • How is the function f(x) defined for x greater than or equal to zero?

    -For x greater than or equal to zero, f(x) is defined as the cosine of pi x.

  • What is the purpose of splitting the definite integral from negative one to one into two parts?

    -The purpose of splitting the definite integral is to simplify the process by separating the regions where the function f(x) has different definitions.

  • What is the antiderivative of x plus one with respect to x?

    -The antiderivative of x plus one with respect to x is x squared over two plus x.

  • How do you evaluate the definite integral from negative one to zero of f(x) dx?

    -By evaluating the antiderivative of x plus one at zero and negative one, the definite integral from negative one to zero is found to be positive 1/2.

  • What is the antiderivative of cosine of pi x with respect to x?

    -The antiderivative of cosine of pi x with respect to x is sine of pi x.

  • How can you apply u-substitution to the integral of cosine of pi x?

    -By setting u equal to pi x and using the chain rule, you can determine that the derivative of sine of pi x with respect to x is pi cosine of pi x, leading to the antiderivative being sine of pi x.

  • What is the result of the definite integral from zero to one of cosine of pi x dx?

    -The definite integral from zero to one of cosine of pi x dx evaluates to zero, as sine of pi times one minus sine of pi times zero equals zero.

  • What is the final result of the definite integral from negative one to one of f(x) dx?

    -The final result of the definite integral from negative one to one of f(x) dx is 1/2, as the sum of the two parts (1/2 and 0) equals 1/2.

  • Why is it important to split the integral at x equals zero?

    -Splitting the integral at x equals zero is important because it is the point where the function f(x) changes its definition, and this helps in evaluating the integral of each piece separately.

  • How does the chain rule help in finding the antiderivative of cosine of pi x?

    -The chain rule helps in finding the antiderivative of cosine of pi x by allowing us to differentiate the composite function sine of pi x, which results in pi cosine of pi x as the derivative, leading to the antiderivative being sine of pi x.

Outlines
00:00
Piecewise Function Integration 📚

This paragraph discusses the process of evaluating the definite integral of a piecewise function. The function is defined as f(x) = x + 1 for x < 0 and f(x) = cos(πx) for x ≥ 0. The integral is evaluated from -1 to 1, and it's noted that the function changes at x = 0. The definite integral is split into two parts to simplify the process: from -1 to 0 and from 0 to 1. The antiderivative of the first part (x + 1) is found to be (x^2/2) + x, and when evaluated from -1 to 0, it results in a value of 1/2. The second part involves the function cos(πx), and the technique of u-substitution is introduced to find its antiderivative, which is sin(πx). However, after applying the chain rule and adjusting for the factor of π, the derivative of sin(πx) is identified as πcos(πx), leading to the antiderivative being 1/π * sin(πx). When evaluated from 0 to 1, this integral evaluates to 0, as sin(π) - sin(0) equals 0.

05:02
Result of the Definite Integral 📈

In this paragraph, the results of the previously calculated integrals are combined to find the total definite integral from -1 to 1 of the piecewise function. The first part of the integral, which is from -1 to 0, evaluates to 1/2. The second part, from 0 to 1, evaluates to 0 because of the properties of the sine function. Therefore, the combined result of the definite integral is 1/2 + 0, which simplifies to 1/2. This final value represents the area under the curve of the piecewise function between -1 and 1 on the x-axis.

Mindmap
Keywords
💡Piecewise function
A piecewise function is a mathematical function that is defined by multiple sub-functions for different intervals or 'pieces' of its domain. In the video, the function f(x) is defined piecewise: for x < 0, f(x) = x + 1, and for x ≥ 0, f(x) = cos(πx). This concept is crucial for understanding how to evaluate the definite integral of the function over the interval from -1 to 1, as it requires splitting the integral into two parts corresponding to the different definitions of the function.
💡Definite integral
A definite integral is a fundamental concept in calculus that represents the accumulated area under a curve of a function over a specified interval. In the video, the goal is to evaluate the definite integral of the piecewise function f(x) from -1 to 1. The process involves finding the antiderivative of the function for each interval and then applying the Fundamental Theorem of Calculus to find the net area.
💡Antiderivative
An antiderivative, also known as an indefinite integral, is a function whose derivative is the original function. In the context of the video, finding the antiderivative of the piecewise function f(x) is necessary to evaluate the definite integral. For the first interval (-1 to 0), the antiderivative is x^2/2 + x, and for the second interval (0 to 1), it involves a u-substitution technique to find the antiderivative of cos(Ï€x).
💡u-substitution
u-substitution is a technique used in calculus to evaluate integrals by transforming them into a more manageable form. It involves replacing the integrand with a new variable (u) that is a function of the original variable (x), and then performing the integral with respect to u. In the video, u-substitution is used to evaluate the integral of cos(πx) by setting u = πx, which allows the derivative of sin(πx) to be found and used to solve the integral.
💡Chain rule
The chain rule is a fundamental calculus technique used to find the derivative of a composite function. It states that the derivative of a function composed of two or more functions is the product of the derivative of the outer function evaluated at the inner function, and the derivative of the inner function. In the video, the chain rule is implicitly used to find the derivative of sin(πx) with respect to x, which is πcos(πx).
💡Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus is a key result that connects the concepts of differentiation and integration. It states that if a function is continuous on the interval [a, b] and F(x) is an antiderivative of the function on that interval, then the definite integral of the function from a to b is equal to F(b) - F(a). This theorem is used in the video to evaluate the definite integral of the piecewise function by finding the antiderivative and evaluating it at the bounds of the interval.
💡Cosine function
The cosine function is a trigonometric function that describes periodic changes in a right-angled triangle or periodic waves. In the video, the cosine function is part of the piecewise definition of f(x) for x ≥ 0, where f(x) = cos(πx). The integral of the cosine function is evaluated using u-substitution and the properties of trigonometric functions.
💡Sine function
The sine function is a trigonometric function that, like the cosine function, describes periodic changes and is used to model oscillatory phenomena. In the context of the video, the sine function is relevant when evaluating the integral of cos(Ï€x) using u-substitution, where the derivative of sin(Ï€x) is needed. The relationship between the sine and cosine functions is used to find the antiderivative of cos(Ï€x).
💡Trigonometric functions
Trigonometric functions, including sine and cosine, are mathematical functions that relate the angles and sides of a right-angled triangle. They are also used to analyze periodic phenomena. In the video, both sine and cosine functions are integral to understanding and evaluating the piecewise function's integral. The properties of these functions are used to find the antiderivative and evaluate the integral.
💡Evaluation
In mathematics, evaluation refers to the process of determining the value of an expression or function at a specific point or for a given input. In the video, evaluation is used to find the values of the antiderivative at the bounds of the integration interval (-1 and 1) to calculate the definite integral. The process involves substituting the bounds into the antiderivative and simplifying the result.
💡Area under the curve
The area under the curve of a function is a geometric concept that represents the quantity being sought when evaluating a definite integral. It corresponds to the portion of the graph of the function that lies between the x-axis and the curve over a specified interval. In the video, the definite integral of the piecewise function represents the area under the curve from -1 to 1, which is calculated by breaking the integral into two parts and summing their areas.
Highlights

The definite integral of a piecewise function is evaluated by splitting the integration interval.

The function f(x) is defined piecewise: f(x) = x + 1 for x < 0 and f(x) = cos(πx) for x ≥ 0.

The definite integral from negative one to one of f(x) dx is split into two integrals: one from negative one to zero and another from zero to one.

The antiderivative of x + 1 is found by incrementing the exponent and dividing by the new exponent.

The antiderivative of x + 1 is evaluated at zero and negative one to find the definite integral from negative one to zero.

The definite integral from negative one to zero evaluates to positive 1/2.

The antiderivative of cos(πx) is found using the chain rule and the fact that the derivative of sin(πx) is πcos(πx).

The integral from zero to one of cos(πx) dx is evaluated using u-substitution with u = πx.

The derivative of sin(πx) with respect to x is πcos(πx), which is used to find the antiderivative of cos(πx).

The antiderivative of cos(πx) is sine of πx, and the integral from zero to one is evaluated by substituting the limits into the antiderivative.

The integral from zero to one of cos(πx) evaluates to zero because sine of π and zero both equal zero.

The final result of the definite integral from negative one to one is 1/2, combining the results from both intervals.

The method of splitting the integral into intervals is useful for handling piecewise functions with different expressions.

The use of u-substitution and the chain rule is demonstrated for dealing with trigonometric functions in integral calculus.

The process of evaluating definite integrals involves finding antiderivatives and applying the Fundamental Theorem of Calculus.

This transcript provides a step-by-step guide on evaluating a definite integral involving a piecewise function and trigonometric substitution.

The importance of correctly applying the limits of integration when evaluating antiderivatives is emphasized.

The transcript showcases the application of calculus techniques in solving mathematical problems involving piecewise-defined functions.

Transcripts

Browse More Related Video

Fundamental Theorem of Calculus: Changing the Bounds with u-Substitution

The Definite Integral Part III: Evaluating From The Definition

Definite integral of absolute value function | AP Calculus AB | Khan Academy

AP Calculus AB Crash Course Day 8 - Integration and Riemann Sums

Periodic Definite Integral

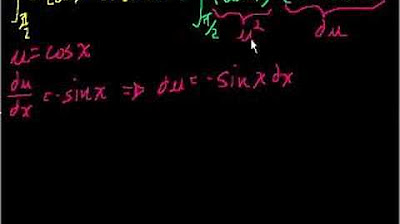
Definite integral with substitution

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsPiecewise FunctionsIntegral CalculusEducational ContentMath TutorialDeductive ReasoningTrigonometryAntiderivativeMathematics EducationOnline Learning