_-substitution intro | AP Calculus AB | Khan Academy

Khan Academy
28 Dec 201205:11
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the process of solving a complex indefinite integral using u-substitution, a technique akin to unwinding the chain rule. It explains how recognizing the derivative of the polynomial in the integrand leads to setting up u as the integral expression itself. By rewriting the integral in terms of u and applying the exponential function's property of being its own antiderivative, the solution is simplified and the constant of integration is included. The final step involves unsubstituting to express the result in terms of x, demonstrating the power of u-substitution in simplifying complex integrals.

Takeaways
  • 📚 The indefinite integral involves a polynomial multiplied by an exponential expression.
  • 🤔 The complexity of the integral suggests the use of u-substitution as a solution technique.
  • 🧠 The intuition for u-substitution comes from unwinding the chain rule, which is a fundamental calculus concept.
  • 🔄 Recognizing that the derivative of the polynomial (x^3 + x^2) is the same as the expression being multiplied by e^x is crucial for applying u-substitution.
  • 🎯 Setting u equal to x^3 + x^2 allows us to rewrite the integral in terms of u, simplifying the problem.
  • 📈 The derivative of u with respect to x is 3x^2 + 2x, which is found by differentiating the polynomial.
  • 🔄 The differential form du = (3x^2 + 2x) dx is obtained by multiplying both sides of the u equation by dx.
  • 📊 The integral can be rewritten in terms of u, with du replacing the original dx, leading to a more recognizable indefinite integral form.
  • 🌟 The antiderivative of e^u with respect to u is simply e^u, which is a basic property of exponential functions.
  • 🔄 Unsubstituting u back into the solution gives us the final antiderivative in terms of x, including the constant factor c.
  • 💡 Verifying the solution by differentiating the antiderivative and applying the chain rule should yield the original integrand.
Q & A

  • What is the integral given in the script?

    -The integral given in the script is ∫(3x^2 + 2x)e^(x^3 + x^2) dx.

  • Why is the integral considered complicated?

    -The integral is considered complicated because it involves a polynomial being multiplied by an exponential expression, and the exponent itself is another polynomial.

  • What technique is suggested for solving the integral?

    -U-substitution is suggested as the technique for solving the integral.

  • How does u-substitution relate to the chain rule?

    -U-substitution is essentially unwinding the chain rule, which helps in simplifying the complex integral by separating the variables and the function.

  • What is the insight that leads to using u-substitution in this case?

    -The insight is recognizing that the derivative of the expression x^3 + x^2 (which is 3x^2 + 2x) is present in the integral, indicating that u-substitution could simplify the problem.

  • What is u set equal to in this context?

    -In this context, u is set equal to x^3 + x^2.

  • What is the derivative of u with respect to x?

    -The derivative of u with respect to x is du/dx = 3x^2 + 2x.

  • How is the integral rewritten using u-substitution?

    -The integral is rewritten as ∫(3x^2 + 2x) dx * e^(u), where u = x^3 + x^2.

  • What is the antiderivative of e^u in terms of u?

    -The antiderivative of e^u in terms of u is e^u + C (where C is the constant of integration).

  • How is the final answer expressed in terms of x?

    -The final answer, in terms of x, is e^(x^3 + x^2) + C.

  • What is the significance of taking the derivative of the final answer?

    -Taking the derivative of the final answer and using the chain rule will lead you back to the original function, confirming that the antiderivative is correct.

Outlines
00:00
📚 Solving a Complex Indefinite Integral Using u-Substitution

The paragraph discusses the process of solving a complex indefinite integral involving a polynomial multiplied by an exponential function. The speaker introduces the integral, which includes 3x squared plus 2x times e, to the power of (x cubed plus x squared), and dx. The key insight is to use u-substitution, a technique akin to unwinding the chain rule. The speaker explains that the exponent part of the integral, x cubed plus x squared, is a derivative of the same expression, which is a clue to apply u-substitution. By setting u as x cubed plus x squared, the speaker proceeds to find the derivative of u with respect to x, which is 3x squared plus 2x. This leads to rewriting the integral in terms of du, and then isolating du to simplify the integral. The speaker then integrates the exponential function with respect to u, finds the antiderivative, and finally subs back to x to obtain the final result, including the constant of integration, c.

05:00
🔄 Verifying the Solution by Taking the Derivative

The second paragraph encourages the audience to verify the solution by taking the derivative of the found antiderivative. The speaker suggests that by doing so, one would use the chain rule and end up with the original integral expression, thereby confirming the correctness of the solution. This step is meant to reinforce the understanding of the relationship between integration and differentiation, and the utility of the chain rule in verifying complex integral solutions.

Mindmap
Keywords
💡indefinite integral
An indefinite integral represents the process of finding the antiderivative, or the reverse process of differentiation, of a given function. In the context of the video, the indefinite integral is the main focus as the goal is to solve for the antiderivative of the complex function 3x^2 + 2x * e^(x^3 + x^2). The process involves identifying the appropriate technique, such as u-substitution, to simplify the integral and find the antiderivative.
💡u-substitution
U-substitution is a technique used in calculus to simplify the process of finding the integral of a complex function. It involves setting a part of the integrand equal to a new variable, u, and then using the derivative of u with respect to x to rewrite the integral in terms of du and the new function of u. This method often makes the integral easier to solve by transforming it into a more familiar or simpler form.
💡chain rule
The chain rule is a fundamental calculus concept used to find the derivative of a composite function. It states that the derivative of a function that is made up of other functions is the product of the derivative of the outer function evaluated at the inner function, and the derivative of the inner function. In the context of the video, the chain rule is analogous to u-substitution, as it involves working with the derivatives of related functions.
💡derivative
A derivative is a mathematical concept that represents the rate of change or the slope of a function at a particular point. In the process of integration, derivatives are used to find the original function by reversing the process of differentiation. The video script discusses the derivatives of the terms within the integrand, such as the derivative of x^3 being 3x^2 and the derivative of x^2 being 2x, which are crucial for applying u-substitution.
💡antiderivative
An antiderivative, also known as an indefinite integral, is a function whose derivative is equal to the given function. The process of finding an antiderivative is called integration. In the video, the main goal is to find the antiderivative of the complex function 3x^2 + 2x * e^(x^3 + x^2), which is achieved through the method of u-substitution.
💡exponential expression
An exponential expression is a mathematical expression that involves a base raised to a power. In the context of the video, the exponential expression e^(x^3 + x^2) is part of the integrand that needs to be integrated. Exponential functions are important in calculus because they often appear in the solutions to differential equations and can be transformed using integration techniques like u-substitution.
💡polynomial
A polynomial is a mathematical expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. In the video, the polynomials 3x^2 and x^3 + x^2 are part of the integrand that the video aims to integrate.
💡differential form
Differential form refers to the representation of a function in terms of its differential, denoted as du or dx, which is the infinitesimal change in the function. In calculus, differential forms are used to express relationships between variables and their rates of change, and they are particularly useful in integration and differentiation.
💡integration
Integration is the process of finding a function whose derivative is a given function, the integral. It is the reverse operation of differentiation and is a fundamental concept in calculus. The video focuses on the method of integration, specifically using u-substitution to solve a complex integral involving polynomials and exponential functions.
💡constant of integration
The constant of integration, often denoted as C, is an additional term that appears in the antiderivative of a function. It accounts for the fact that the derivative of a constant is zero, and thus, there can be multiple antiderivatives that differ by a constant. In the context of the video, after finding the antiderivative e^u, the constant of integration is added to account for the possibility of different constant terms in the family of functions that are antiderivatives of the integrand.
💡unsubstitute
Unsubstitute is the process of replacing the new variable introduced during u-substitution back with the original expression for which the integral was being solved. This step transforms the solution in terms of the new variable (u) back into the solution in terms of the original variable (x).
Highlights

The indefinite integral involves a polynomial multiplied by an exponential expression.

The key insight for solving this integral is recognizing the opportunity to use u-substitution.

U-substitution essentially unwinds the chain rule, which is a fundamental calculus technique.

The derivative of the polynomial x^3 + x^2 is recognized as a clue to apply u-substitution.

By setting u as x^3 + x^2, the derivative du/dx is calculated as 3x^2 + 2x.

The integral can be rewritten in differential form, showing du as a function of dx.

The integral is transformed to a more recognizable form by substituting du for the differential expression.

The new integral expression features e^(u), which simplifies the process of finding the antiderivative.

The antiderivative of e^(u) with respect to u is e^(u), plus a constant factor.

The final step involves unsubstituting u back into the expression in terms of x.

The antiderivative is found to be e^(x^3 + x^2) + C, demonstrating the power of u-substitution.

The process showcases the utility of recognizing patterns in calculus problems to simplify complex integrals.

The method also emphasizes the importance of understanding the chain rule and its applications in calculus.

The example serves as a practical application of u-substitution, which is a valuable technique in solving advanced calculus problems.

The transcript provides a detailed walkthrough of the steps involved in u-substitution, which is beneficial for educational purposes.

The explanation encourages users to verify the solution by taking the derivative, reinforcing the understanding of calculus concepts.

The transcript's detailed explanation and step-by-step approach make it a valuable resource for learning and teaching calculus.

Transcripts

Browse More Related Video

_-substitution: definite integrals | AP Calculus AB | Khan Academy

Back Substitution - When a u-sub doesn't match cleanly!

(2^ln x)/x Antiderivative Example

Integration Of Exponential Functions [ Substitution Method ]

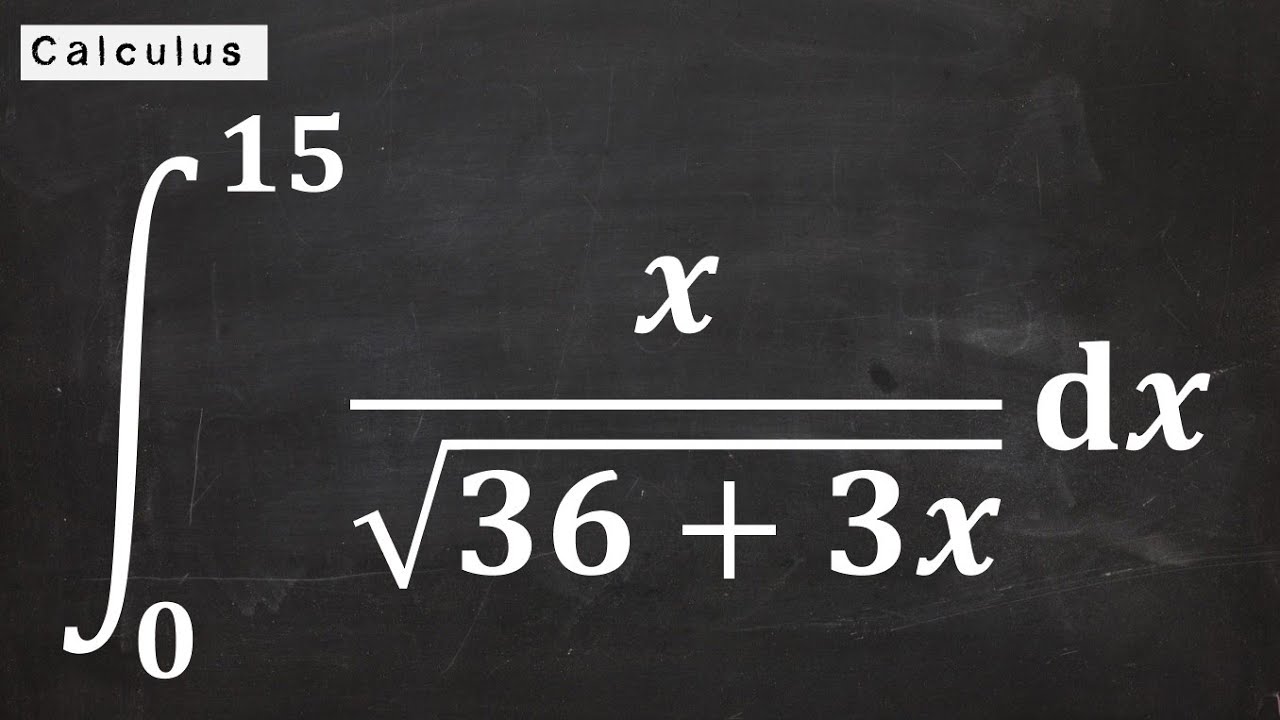
Definite Integral With U-Substitution

_-substitution: rational function | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsCalculusIntegrationu-SubstitutionPolynomial FunctionsExponential FunctionsDerivative ConceptsEducational ContentMath TutorialAdvanced Math