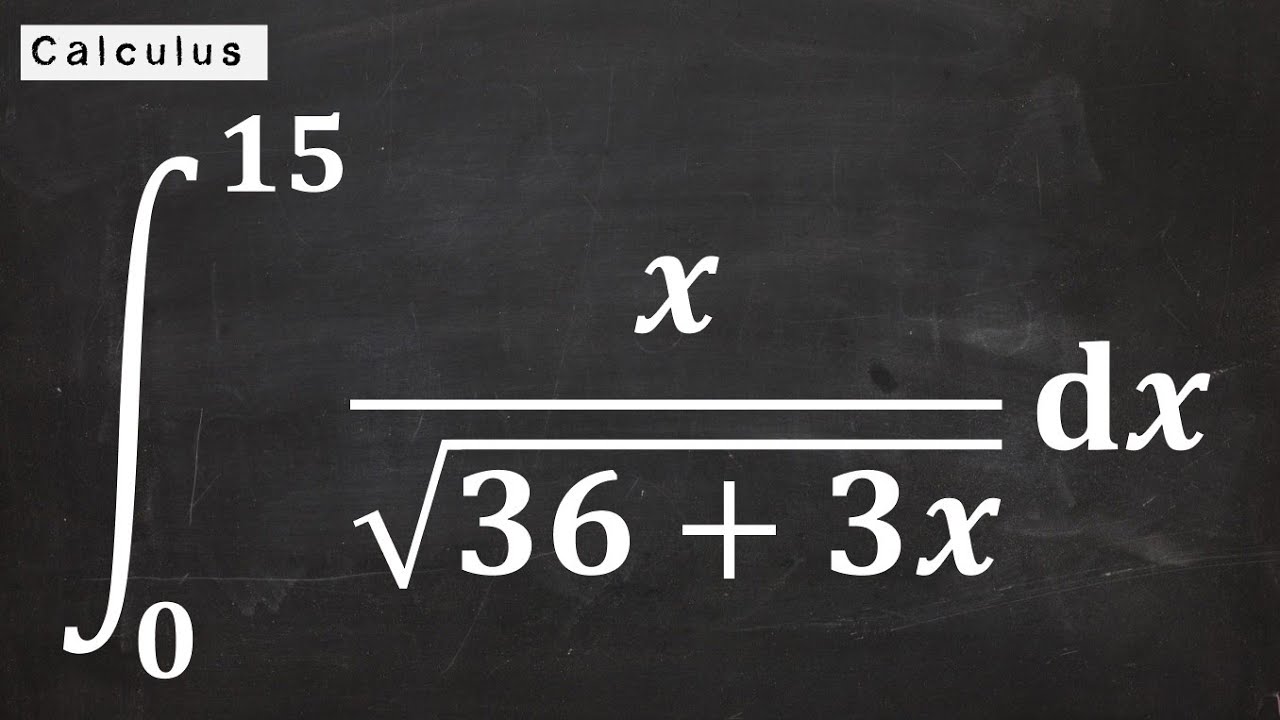_-substitution: defining _ | AP Calculus AB | Khan Academy
TLDRThe video script introduces the concept of u-substitution, a technique used in calculus to simplify the process of integration. It emphasizes the importance of recognizing when u-substitution is appropriate and how to define the variable 'u'. The script uses the example of integrating a function involving a square root of a polynomial in x to illustrate the steps of u-substitution, including identifying the inside function, finding its derivative, and rewriting the integral in terms of 'u' and 'du'. The goal is to transform the integral into a more manageable form, making it easier to evaluate using standard integration techniques.
Takeaways
- 📘 The video focuses on practicing the first step of u-substitution, which is recognizing when it is appropriate to use.
- 🔍 The first step in u-substitution is to identify patterns in the integral that resemble the chain rule.
- 🧠 Remembering the chain rule is crucial: the derivative of a composite function is the outer function's derivative times the inner function's derivative.
- 🌟 The goal of u-substitution is to simplify the integral by transforming the problem into a simpler form where the derivative of the inner function is evident.
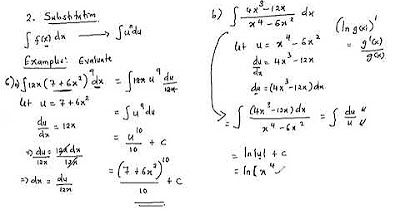
- 📌 An example given is the indefinite integral of (2x + 1) * sqrt(x^2 + x) dx, where u-substitution can be applied.
- 👉 If we set u = x^2 + x, the derivative du/dx = 2x + 1, which matches the pattern we're looking for.
- 🤝 By treating differentials like variables, we can rewrite the integral as ∫(sqrt(u) * (2x + 1) dx), which simplifies the process.
- 📈 The integral can be further rewritten to emphasize the product of its components, making it clearer how u-substitution simplifies the problem.
- 🎯 After substitution, we can evaluate the integral using the power rule, specifically the reverse power rule.
- 🔄 Finally, we reverse substitute the x expression back in for u to find the antiderivative.
Q & A
What is the main topic of the video?
-The main topic of the video is practicing the first step of u-substitution in integration, specifically recognizing when u-substitution is appropriate and defining an appropriate u.
What is u-substitution used for in calculus?
-U-substitution is used to simplify the process of integration by transforming a complex integral into a more manageable one, often by undoing the chain rule.
How can we identify when to use u-substitution?
-We can identify when to use u-substitution by looking for a pattern inside the integral that resembles a composite function, where the derivative of the inside function is being multiplied.
What is the chain rule in calculus?
-The chain rule states that the derivative of a composite function, f(g(x)), with respect to x, is equal to the derivative of the outside function (f') evaluated at the inside function (g(x)) times the derivative of the inside function (g'(x)).
In the given example, what is the integral we are trying to evaluate?
-The integral we are trying to evaluate is the indefinite integral of (2x + 1) times the square root of (x^2 + x) with respect to x, denoted as ∫(2x + 1)√(x^2 + x) dx.
How do we define u in the context of the example provided?
-In the example, we define u as x^2 + x, since it is the expression inside the square root that we can differentiate to get the term 2x + 1.
What is the derivative of u with respect to x in the example?
-The derivative of u with respect to x, where u = x^2 + x, is 2x + 1.
How can we rewrite the integral using u and du?
-We can rewrite the integral as ∫√u * du, where u = x^2 + x and du = (2x + 1)dx, simplifying the process of finding the antiderivative.
What is the reverse power rule in integration?
-The reverse power rule states that the integral of a function f(x)^n (where n is a constant) is (f(x)^(n+1))/(n+1) + C, where C is the constant of integration.
How do we reverse substitute after finding the antiderivative?
-After finding the antiderivative, we reverse substitute by replacing the u variable back with its original x expression to get the final answer in terms of x.
What is the significance of u-substitution in solving integrals?
-U-substitution is significant in solving integrals as it often simplifies complex integration problems by breaking them down into more straightforward calculations, making the process more manageable and easier to understand.
Outlines
📚 Introduction to u-Substitution
This paragraph introduces the concept of u-substitution, a technique used in calculus for evaluating integrals. The tutor explains that the first step in u-substitution, recognizing when it's appropriate, can be challenging for beginners. The paragraph presents an example of finding the indefinite integral of a function and illustrates how to identify when u-substitution can be applied. The tutor guides the viewer through the process of defining an appropriate u by examining the derivative of the function inside the integral.
Mindmap
Keywords
💡u substitution
💡indefinite integral
💡chain rule
💡derivative
💡composite function
💡antiderivative
💡integration
💡square root
💡algebraic expression
💡reverse power rule
💡anti-derivative
Highlights
The video focuses on practicing the first step of u substitution, which is recognizing when it is appropriate to use.
An example is given to illustrate the process, involving the indefinite integral of a function involving a square root and a linear term.
The chain rule is introduced as a foundational concept to understand u substitution, highlighting its role in the differentiation process.
The video emphasizes the importance of identifying a pattern within the integral that resembles the chain rule for u substitution to be applicable.
A specific function, x squared plus x, is chosen as the potential u, and its derivative is calculated to determine the substitution.
The derivative of the chosen u (x squared plus x) is found to be two x plus one, which is key for the u substitution process.
The concept of treating differentials like variables or numbers is introduced to facilitate the substitution process.
The integral is rewritten to reflect the u substitution, showing the product of three distinct terms for clarity.
The integral is then reformulated to express it in terms of u and du, simplifying the evaluation process.
The video suggests the possibility of rewriting the integral in a less conventional but legitimate way to better illustrate the u substitution.
The concept of the reverse power rule is introduced as a tool to evaluate the integral after the u substitution.
The process of reversing the substitution to find the antiderivative in terms of x is explained.
The video encourages pausing and thinking about the problem before proceeding, promoting active engagement with the material.
The video's approach to explaining u substitution is methodical, breaking down complex concepts into manageable parts.
The practical application of u substitution in solving integrals is demonstrated, making the concept more accessible.
The video highlights the mathematical flexibility in rearranging terms within the integral to facilitate the substitution process.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: