Math 1325 Lecture 9 6 Chain & Power Rule
TLDRThis transcript is from a calculus lecture focusing on the chain rule, particularly relevant for business and social science students. The lecturer begins by reviewing composite functions, using an everyday example of hourly wage and taxes to illustrate the concept. They then introduce the chain rule for finding derivatives of composite functions, emphasizing the strategy of 'working from the outside in.' The rule is further explained through various examples, including simplifying expressions and applying the rule to more complex scenarios. A unique analogy likens the chain rule to dining at a fancy restaurant, suggesting to start with the outer function and progressively work towards the inner function. The lecture also tackles an applied problem involving the relationship between the length and weight of fish, guiding students on how to use the chain rule to find the rate of growth in weight with respect to length. The summary underscores the importance of attention to detail and methodical approach in solving calculus problems, highlighting the chain rule's utility in both abstract and real-world applications.
Takeaways
- 📚 **Composite Functions**: Functions are often stacked, where the output of one function (G of X) becomes the input to another (F of G of X).
- 💼 **Real-World Example**: An example of a composite function is an hourly wage where the gross pay is processed through a tax and benefits function to determine net pay.
- 🔢 **Function G and F**: G is a function that squares the input and adds 2 (G of X = X^2 + 2), while F doubles the input and subtracts 3 (F of X = 2X - 3).
- 🧮 **Derivative of Composite Functions**: To find the derivative, substitute the inner function (G of X) into the outer function (F) and then apply algebra.
- 📉 **Chain Rule**: The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function.
- 🍴 **Chain Rule Analogy**: Think of the chain rule like eating at a fancy restaurant; start from the outside (outer function) and work your way in (inner function).
- 🔑 **Identifying Outer and Inner Functions**: In composite functions, the outer function operates on the result of the inner function, which is often indicated by parentheses.
- 📌 **Substitution with 'u'**: The chain rule often involves substituting the inner function with a variable 'u' for simplicity in finding derivatives.
- 📐 **Power Rule Application**: When applying the chain rule, the power rule is used to find the derivative of the outer function, treating the inner function as a single entity.
- 🔄 **Simplifying Expressions**: After applying the chain rule, simplify the expression by combining like terms and reducing where possible.
- ⚖️ **Allometric Relationships**: An example problem involves using the chain rule to find the rate of growth of a fish's weight in relation to its length, given an allometric relationship and a growth rate formula.
Q & A
What is a composite function in the context of calculus?
-A composite function in calculus is a function that is formed by using one function within another. It is represented as f(G(x)), where G is the inner function and f is the outer function.
How does the concept of composite functions relate to real-life scenarios?
-Composite functions can be related to real-life scenarios such as calculating an hourly wage where the gross pay is first computed and then subjected to a tax and benefit function to determine the net pay.
What is the chain rule in calculus?
-The chain rule is a fundamental rule in calculus for differentiating composite functions. It states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function.
Can you provide an example of how to apply the chain rule?
-An example of applying the chain rule is given by the functions f(x) = 3x^2 and G(x) = 2x - 1. The composite function is f(G(x)) = 3(2x - 1)^2. Using the chain rule, the derivative is found by taking the derivative of the outer function (3 times the square of the inner function) and multiplying it by the derivative of the inner function (2x - 1), which results in 12x - 6.
What is the process of finding the derivative of a composite function using the chain rule?
-To find the derivative of a composite function using the chain rule, first identify the outer and inner functions. Then, take the derivative of the outer function with respect to the inner function (keeping the inner function as a whole), and multiply it by the derivative of the inner function with respect to the original variable (x).
How can one simplify the process of applying the chain rule?
-One can simplify the process by using an analogy such as eating at a fancy restaurant, where you start from the outside and work your way in. This means taking the derivative of the outer function first, and then multiplying by the derivative of the inner function.
What is the relationship between the length and weight of a species of fish in the Pacific Ocean, as given in the script?
-The relationship between the length (L in meters) and weight (W in kilograms) of a species of fish in the Pacific Ocean is given by the formula W = 10.375 * L^3.
What is the rate of growth in length of a fish, as given in the script?
-The rate of growth in length of a fish, given in the script, is represented by the formula dL/dt = 0.36 - 0.18L, where L is the length of the fish and t is time in years.
How can you find the rate of growth in weight of a fish, given its weight and the rate of growth in length?
-To find the rate of growth in weight (dW/dt), you first need to express the weight (W) in terms of length (L) using the given relationship between W and L. Then, you differentiate this relationship to find dW/dL. Finally, you use the chain rule to find dW/dt by multiplying dW/dL by the rate of growth in length dL/dt.
What is the formula for the rate of growth in weight of a fish in terms of its length?
-The formula for the rate of growth in weight (dW/dt) in terms of length (L) is derived from the chain rule and is given by dW/dt = (dW/dL) * (dL/dt), which simplifies to 11.205L^2 - 5.6025L^3 when substituting the given expressions for dW/dL and dL/dt.
How can you approximate the rate of growth in weight of a fish that weighs 30 kilograms?
-To approximate the rate of growth in weight for a fish that weighs 30 kilograms, first find the length (L) corresponding to that weight using the weight-length relationship W = 10.375 * L^3. Then, substitute the value of L into the formula for the rate of growth in weight (dW/dt) to find the approximate rate of weight growth at that length.
Outlines
😀 Introduction to Composite Functions and the Chain Rule
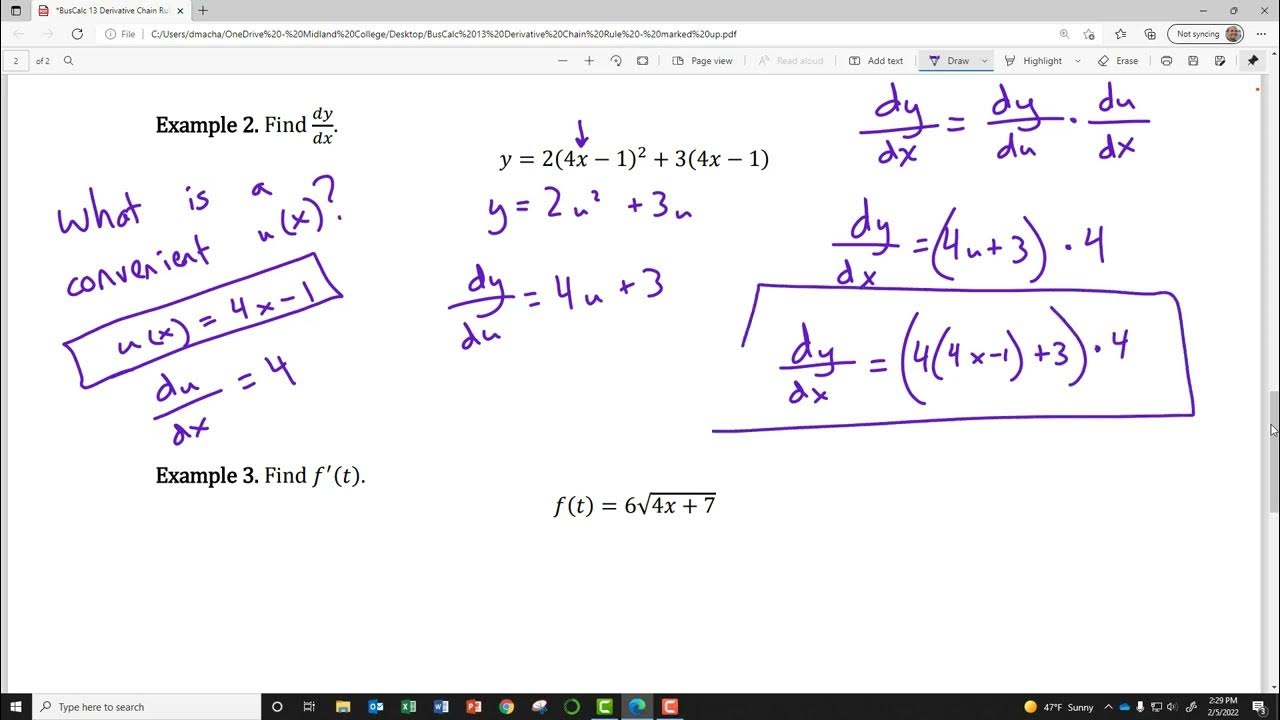
This paragraph introduces the concept of composite functions and the chain rule in the context of calculus for business and social science. It explains that composite functions are functions 'stacked' on one another, where the output of one function becomes the input for the next. The paragraph uses the example of an hourly wage to illustrate how composite functions work in real life. It also presents a simple mathematical example involving squaring the input and adding 2, followed by doubling the result and subtracting 3, to demonstrate the process of finding the derivative of a composite function. The chain rule is introduced as a method for finding derivatives of such functions, emphasizing the need to differentiate the outer function with respect to an intermediate variable (u), and then multiply by the derivative of the inner function with respect to the original variable (x).
📚 Applying the Chain Rule to Find Derivatives
The second paragraph delves deeper into the application of the chain rule for finding derivatives. It uses the example of a composite function involving the square of a linear function to demonstrate the process. The paragraph emphasizes the importance of identifying the outer and inner functions and uses substitution with a variable 'u' for the inner function. It also provides a step-by-step guide on how to apply the chain rule, including setting up the derivative of the outer function, multiplying by the derivative of the inner function, and simplifying the result. The analogy of eating at a fancy restaurant is used to help students remember to start with the outer function and work their way inwards to the inner function.
🧮 Advanced Chain Rule Problems and Allometric Relationships
The third paragraph presents more complex applications of the chain rule, including a real-world example involving the relationship between the length and weight of a species of fish in the Pacific Ocean. The problem provides an allometric relationship and a rate of growth for the length of the fish and asks for the rate of growth of the weight in terms of length. The paragraph demonstrates how to use the chain rule to find the derivative of the weight with respect to time, given the derivative of the length with respect to time. It also emphasizes the importance of careful reading and understanding of the problem, as well as the need to use proper notation to avoid confusion.
🔍 Solving for Rate of Growth in Weight Using Chain Rule
This paragraph focuses on solving a specific problem related to the rate of growth in weight of a fish given its weight. It outlines the steps to find the length of the fish when it weighs 30 kilograms, using the provided formula that relates weight to length. The paragraph cautions against common mistakes, such as confusing weight with length, and stresses the importance of attention to detail. It then guides through the process of substituting the known values into the derived formula to approximate the rate of growth in weight for the fish.
📘 Final Thoughts on Problem-Solving and Attention to Detail
The final paragraph emphasizes the importance of careful problem-solving and attention to detail, especially in calculus. It reminds students to be methodical and to use scratch paper and proper notation to avoid errors. The paragraph also encourages students to fully understand the problem and the formulas involved before attempting to solve it, highlighting the need for precision in fields such as engineering, business, and economics where calculus is applied.
Mindmap
Keywords
💡Chain Rule
💡Composite Functions
💡Derivative
💡Function
💡Algebra
💡Integration
💡Differentiable Functions
💡Exponential Functions
💡Quotient Rule
💡Product Rule
💡Allometric Relationships
Highlights
Composite functions are a fundamental concept in calculus, often representing real-world scenarios where one process follows another.
The chain rule is a method for finding derivatives of composite functions, which are functions within functions.
An example of a composite function is an hourly wage, where the hours worked are input into a payroll function, and the output is then taxed and deducted.
To apply the chain rule, identify the outer function and the inner function, then multiply the derivative of the outer function by the derivative of the inner function.
The chain rule can be intuitively understood through the analogy of eating at a fancy restaurant, starting from the outside and working your way in.
When applying the chain rule, treat the inner function as a single entity (a 'boxed' variable) and differentiate the outer function with respect to this box.
The derivative of a composite function is found by taking the derivative of the outer function with respect to the inner function and multiplying by the derivative of the inner function with respect to the original variable.
The chain rule can simplify complex derivative problems by breaking them down into manageable parts.
When differentiating composite functions, it's crucial to correctly identify the outer and inner functions to apply the chain rule accurately.
The chain rule is not just a mathematical tool but also a strategy for problem-solving, especially in complex or overwhelming problems.
In problems involving rates of change, such as growth rates in biology or economics, the chain rule can be used to relate one rate to another.
When given a formula relating two variables, the chain rule can help find the rate of change of one variable with respect to another.
Careful attention to detail is crucial when applying the chain rule, especially when substituting values into formulas.
The chain rule can be used to find the rate of growth in weight of a fish species in relation to its length, given the rate of growth in length.
Understanding the relationship between variables is key to using the chain rule effectively, as demonstrated in the fish growth problem.
Rewriting complex formulas in a simpler form or using standard notations can make applying the chain rule and solving calculus problems more straightforward.
The chain rule is a versatile mathematical concept that can be applied across various disciplines, from pure mathematics to the sciences and social sciences.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: