Product rule | Taking derivatives | Differential Calculus | Khan Academy

Khan Academy
3 Oct 200708:49
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces viewers to the product rule and chain rule for solving derivatives, essential tools in calculus. By using these rules, one can tackle complex derivative problems by understanding the derivatives of basic functions. The script provides detailed examples, demonstrating how to apply the product rule to a polynomial and how to use the chain rule for more complex functions, highlighting the efficiency of these methods over traditional algebraic manipulation.

Takeaways
  • πŸ“š Introduction to new tools for solving derivatives, focusing on the product rule and chain rule.
  • πŸ”’ Explanation of the product rule with an example: if f(x) = h(x) * g(x), then f'(x) = h'(x)g(x) + h(x)g'(x).
  • πŸ“ˆ Application of the product rule demonstrated with a polynomial function: 5x^5 - x^7 * 20x^2 + 3x^-7.
  • 🌟 Use of the chain rule for composite functions, where f(x) = h(g(x)).
  • 🧠 Breakdown of a complex derivative problem involving multiple terms and the use of both product and chain rules.
  • 🎨 Use of different colors to aid in understanding the differentiation process in the examples.
  • πŸ”„ Step-by-step process of finding the derivative of a function by applying the product and chain rules.
  • πŸ“Š Explanation of how the chain rule allows for the differentiation of inner functions before applying the outer function's derivative.
  • πŸ”‘ Importance of understanding the product and chain rules for tackling a variety of derivative problems.
  • πŸš€ι’„ε‘Š of upcoming topics, including trigonometric functions, natural log, logarithm, and exponential functions.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the introduction and application of the product rule and chain rule for solving derivatives of functions.

  • What is the product rule mentioned in the video?

    -The product rule states that if f(x) = h(x) * g(x), then the derivative f'(x) is equal to the derivative of the first function times the second function plus the first function times the derivative of the second function.

  • How does the chain rule relate to the product rule?

    -The chain rule is a method used to find the derivative of a composite function. It involves taking the derivative of the outer function, multiplying it by the inner function's derivative, and then multiplying by the inner function itself.

  • What is an example of a function that uses the product rule in the video?

    -An example function given in the video is f(x) = 5x^5 - x^7 * (20x^2 + 3x^-7).

  • How does the video demonstrate the application of the product rule?

    -The video demonstrates the application of the product rule by breaking down the given example function into its components, taking the derivative of each component, and then combining them to find the derivative of the entire function.

  • What is the significance of using the product and chain rules in calculus?

    -The product and chain rules are significant in calculus as they provide a systematic way to find the derivatives of more complex functions, especially those that are products or compositions of simpler functions.

  • What is the purpose of changing colors in the video while solving the derivatives?

    -The purpose of changing colors in the video is to visually distinguish between different terms and steps in the process of finding the derivative, making it easier for the viewer to follow along.

  • How does the video suggest the use of these rules for functions other than polynomials?

    -The video suggests that the product and chain rules become even more useful when dealing with derivatives of functions beyond polynomials, such as trigonometric functions, natural logarithms, and exponential functions.

  • What is the next topic the video promises to cover?

    -The next topic the video promises to cover is the application of the product and chain rules to trigonometric functions, natural logarithms, and exponential functions.

  • What is the final outcome of using the chain and product rules in the given examples?

    -The final outcome of using the chain and product rules in the given examples is obtaining the derivative of the complex functions, which allows for the evaluation of the slope of these functions at any point.

  • How does the video emphasize the importance of these rules in solving derivative problems?

    -The video emphasizes the importance of these rules by showing that they allow for the simplification and solving of derivative problems that would otherwise be very complex and time-consuming if done through polynomial expansion and manual algebra.

Outlines
00:00
πŸ“š Introduction to Derivatives and Product Rule

This paragraph introduces the concept of solving derivatives using the product rule and chain rule. It emphasizes the importance of understanding these rules alongside the derivatives of common functions to tackle various derivative problems. The explanation begins with the product rule, detailing how to apply it when the function f(x) is the product of two other functions, h(x) and g(x). The process of finding the derivative of the given function, a polynomial expression, is demonstrated using the product rule. The explanation is further clarified with an example, showcasing the step-by-step application of the product rule to find the derivative of a complex polynomial. The paragraph also mentions the chain rule briefly and sets the stage for more examples and a deeper dive into the product and chain rules.

05:02
🎨 Applying Chain Rule to Complex Functions

This paragraph delves into the application of the chain rule for finding the derivative of complex functions. It introduces a new notation where 'y' is used instead of 'f(x)', and the goal is to find dy/dx. The explanation walks through the process of using the chain rule to find the derivative of a function composed of multiple terms, including polynomials and expressions with negative exponents. The paragraph highlights the use of colors to differentiate between the derivatives of different terms and the process of multiplying these derivatives with their respective terms. The application of the chain rule is demonstrated through a comprehensive example, showing how to break down complex expressions and find their derivatives step by step. The paragraph concludes by emphasizing the usefulness of the chain and product rules, especially when dealing with functions beyond polynomials, and mentions the upcoming topics of trigonometric functions, natural log, logarithm, and exponential functions.

Mindmap
Keywords
πŸ’‘Derivatives
Derivatives are a fundamental concept in calculus that represent the rate of change of a function with respect to its variable. In the context of the video, derivatives are used to solve problems involving the slope of a curve or the rate of change of various mathematical expressions. The video script introduces methods for calculating derivatives, such as the product rule and chain rule, and provides examples of their application to different functions.
πŸ’‘Product Rule
The product rule is a vital calculus formula used to find the derivative of a product of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the video, the product rule is demonstrated through the example of finding the derivative of the function f(x) = 5x^5 - x^7 * 20x^2 + 3x^7.
πŸ’‘Chain Rule
The chain rule is another essential calculus formula used to find the derivative of a composite function, which is a function composed of multiple functions nested within each other. The chain rule involves taking the derivative of the outer function and multiplying it by the derivative of the inner function. The video script illustrates the chain rule with a complex function and emphasizes its utility in simplifying the process of finding derivatives, especially when dealing with composite functions.
πŸ’‘Function
In mathematics, a function is a relation that pairs each element from a set (called the domain) with exactly one element from another set (the range). Functions are central to the video's content as they are the primary objects for which derivatives are calculated. The video discusses various functions and the methods to find their derivatives, showcasing how these derivatives can provide insights into the behavior of the functions.
πŸ’‘Slope
The slope of a curve at a particular point is a measure of how steep the curve is at that point and indicates the rate of change of the function's value with respect to its variable. In the video, the concept of slope is important as it relates to the derivative of a function, which can be thought of as the slope of the tangent line to the curve represented by the function. The video aims to teach how to calculate this slope using derivatives.
πŸ’‘Polynomial
A polynomial is an algebraic expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. Polynomials are important in the video because they are one of the types of functions for which derivatives can be calculated using the product and chain rules. The video provides examples of polynomial functions and demonstrates how to find their derivatives.
πŸ’‘Trigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, are mathematical functions that relate angles to real numbers. They are named after the study of triangle ratios in trigonometry but are used in a wide range of applications, including calculus. Although not explicitly discussed in the provided script, the mention of trigonometric functions suggests that future content will cover their derivatives, which are essential in many calculus problems involving angles and periodic behavior.
πŸ’‘Natural Log
The natural log, or logarithm with base 'e' (where 'e' is the mathematical constant approximately equal to 2.71828), is a key concept in calculus and many other areas of mathematics. It is used to solve equations where the variable is an exponent. In the context of the video, while the natural log is not directly discussed, it is implied that upcoming content will include its derivative, which is crucial for understanding logarithmic functions and their rates of change.
πŸ’‘Logarithm
A logarithm is the inverse operation to exponentiation, and it helps find the exponent to which a given base must be raised to obtain a specific number. Logarithms, like the natural log, are important in calculus for analyzing the growth and decay rates of functions. The video script alludes to future lessons on logarithmic functions and their derivatives, which will be essential for understanding how these functions change with respect to their variable.
πŸ’‘Exponential Functions
Exponential functions are mathematical functions of the form f(x) = a^x, where 'a' is a constant and 'x' is the variable. These functions are characterized by rapid growth or decay and are fundamental in various fields, including finance, physics, and biology. The video script suggests that future content will cover the derivatives of exponential functions, which are crucial for understanding their behavior and rates of change.
πŸ’‘Rate of Change
The rate of change is a measure of how quickly a quantity changes with respect to another quantity. In calculus, the rate of change is often used to describe the instantaneous rate of change of a function at a particular point, which is found by taking the derivative of the function. The video script focuses on teaching methods to calculate derivatives, which are directly related to finding the rate of change of functions.
Highlights

Introduction to a new tool for solving derivatives.

Explaining the product rule and chain rule for derivatives.

Product rule application when f(x) is a product of two functions.

Derivative calculation using the product rule for the function f(x) = 5x^5 - x^7 * (20x^2 + 3x^-7).

Using the product rule to simplify derivative problems.

Example of derivative calculation for f(x) = 10x^3 + 5x^2 - 7 * 20x^8 - 7.

Derivative calculation using the chain rule for complex functions.

Explanation of the chain rule with y = x^2 + 2x^5 * 3x^-3 + x^-7.

Combining the product and chain rules for more complicated derivatives.

Derivative calculation involving exponents and negative powers.

Using derivatives to find the rate of change (slope) of a function.

Potential of simplifying complex functions using the chain and product rules.

Upcoming topics on trigonometric functions, natural log, logarithm, and exponential functions.

The importance of understanding derivatives for various mathematical applications.

The ability to evaluate the slope of a function at any point using derived expressions.

The transcript provides a comprehensive guide on tackling derivative problems using the product and chain rules.

Transcripts

Browse More Related Video

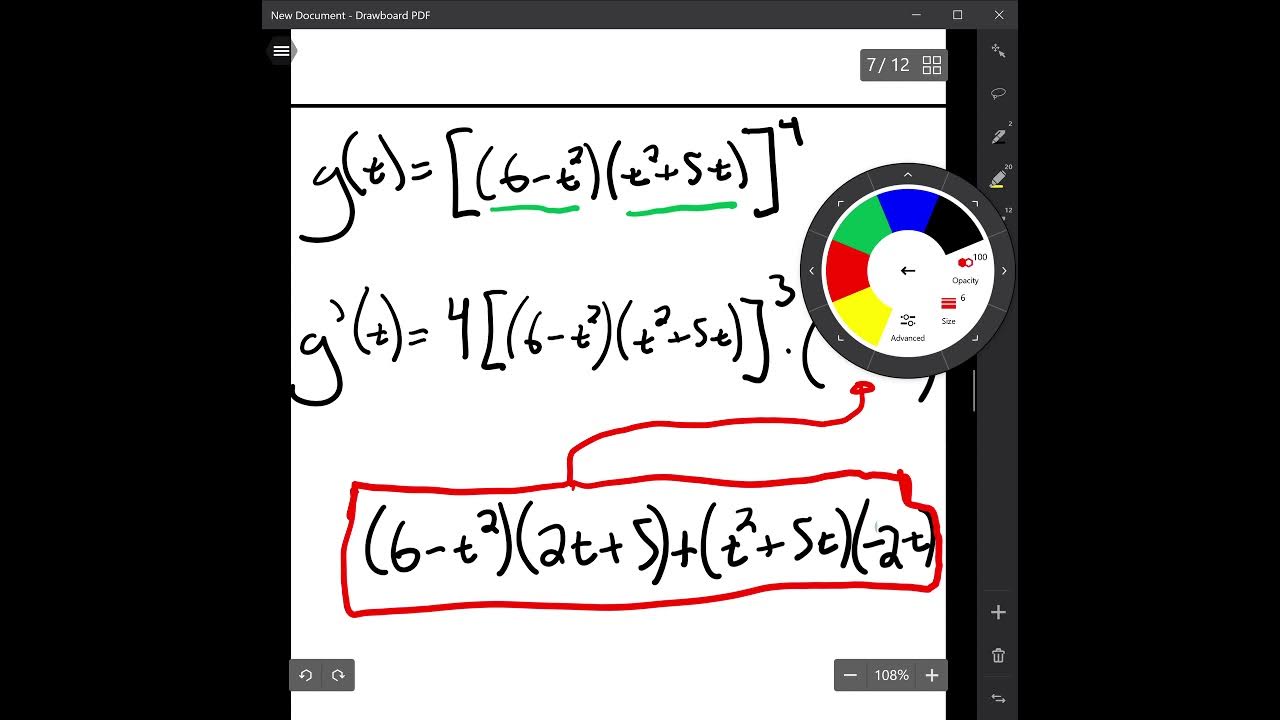
Derivatives with Multiple Rules

Calculus AB Lesson 3.4 The Chain Rule

Derivatives of Trig Functions - Calculus | MCV4U

Visualizing the chain rule and product rule | Chapter 4, Essence of calculus

Math 1325 Lecture 9 7 - Using Derivative Forumulas

Calculus 1 Lecture 2.3: The Product and Quotient Rules for Derivatives of Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DerivativesCalculusProduct RuleChain RuleMathematicsPolynomialsTrigonometricLogarithmsExponentialsEducational