Multivariable Chain Rule (Calculus 3)
TLDRThis video from Houston Math Prep dives into the multi-variable chain rule in calculus, a topic typically covered in Calculus 3. It explains the concept by starting with single-variable functions and progressing to functions of multiple variables, focusing on the total differential and how to apply the chain rule when variables are functions of another variable, such as time. The video uses a tree diagram to illustrate the process of finding derivatives, providing clarity on when to use ordinary versus partial derivatives. It also works through examples to demonstrate the application of the multi-variable chain rule in various scenarios, including cases where intermediate variables are functions of more than one variable.
Takeaways
- 🔗 The video covers the chain rule for multi-variable calculus, typically taught in Calculus 3.
- 🧩 The chain rule for single-variable functions can be found in a linked video.
- 🔄 The concept of differentials and their application in calculus is reviewed.
- 📐 The total differential for a multi-variable function involves partial derivatives with respect to each variable.
- 📉 The multi-variable chain rule is introduced, where variables are functions of another variable, commonly t.
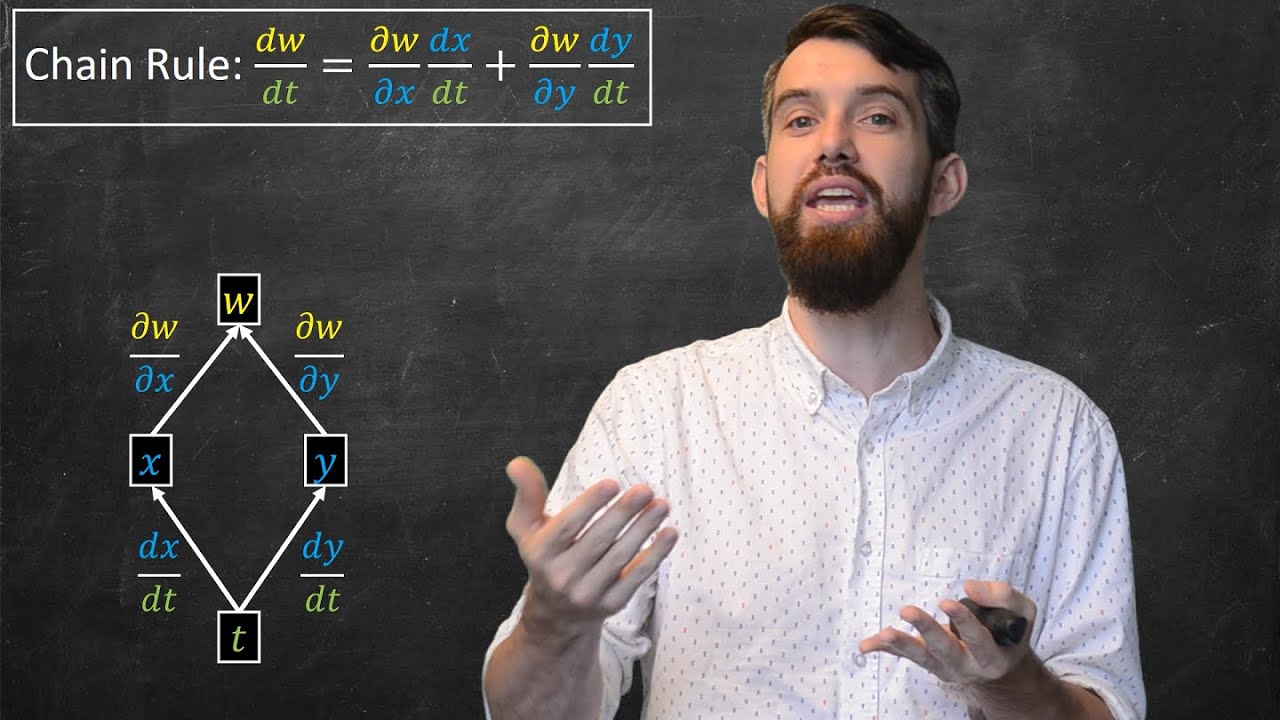
- 🌳 A tree diagram helps visualize the chain rule for functions of multiple variables, clarifying the notation.
- 🧮 Example 1: Calculating dz/dt for a function z = x^3 + y^3 where x = 2sin(t) and y = 3cos(t).
- 📊 Example 2: Handling cases where x and y are functions of two variables, s and t, and setting up the corresponding tree diagram.
- 🔍 Example 3: Calculating partial derivatives dz/ds and dz/dt for z as a function of x and y, and x and y as functions of s and t.
- 🎓 The video emphasizes converting derivatives into terms of the lowest row variables and discusses different ways to express the final answer.
Q & A
What is the main topic of the video?
-The main topic of the video is the chain rule for multi-variable calculus, typically covered in a calculus 3 course.
What is the purpose of the differentials dy and dx in calculus?
-In calculus, differentials dy and dx represent very small changes in y and x, respectively, and are used in various applications such as u-substitution for integration, linear approximations, and solving separable differential equations.
What is the formula for the differential of a function of one variable?
-The formula for the differential of a function of one variable y with respect to x is given by dy = (dy/dx) dx.
How is the differential of a function of multiple variables different from that of a single variable?
-For a function of multiple variables, the differential takes into account small changes in all variables. For example, if z is a function of x and y, the total differential for z is given by dz = (∂z/∂x) dx + (∂z/∂y) dy.
What is the multi-variable chain rule used for?
-The multi-variable chain rule is used to find the derivative of a function with respect to a variable when the function's variables are also expressed in terms of other variables, commonly functions of t.
How can a tree diagram help in understanding the chain rule for multi-variable functions?
-A tree diagram helps visualize the relationships between variables and functions, indicating which derivatives are ordinary or partial, and guides the calculation of the chain rule by showing the paths from the function to the variable of interest.
What does the bottom row of a tree diagram represent in the context of the chain rule?
-The bottom row of a tree diagram represents the variables that are directly involved in the derivative being sought. If there is only one variable in the bottom row, the derivative is an ordinary derivative.
What is the significance of a 'fork' in a tree diagram for the chain rule?
-A 'fork' in a tree diagram indicates a point where a variable is a function of more than one other variable, which means that the derivative at that point will be a partial derivative due to the multiple paths available.
Can you provide an example of how to calculate the derivative of a function with respect to t using the chain rule?
-Sure. Given z = x^3 + y^3, x = 2sin(t), and y = 3cos(t), the derivative of z with respect to t, denoted as dz/dt, is calculated by taking the partial derivative of z with respect to x, multiplying by the derivative of x with respect to t, and adding the partial derivative of z with respect to y, multiplied by the derivative of y with respect to t.
How does the chain rule change when a function's variables are functions of more than one variable?
-When a function's variables are functions of more than one variable, the chain rule becomes more complex, involving multiple partial derivatives and paths in the tree diagram. The derivative with respect to a variable will be a partial derivative, and the calculation will consider all paths leading to the variable of interest.
What is the final step in calculating the derivative using the chain rule for multi-variable functions?
-The final step is to express the result in terms of the variables present in the bottom row of the tree diagram, which represent the variables with respect to which the derivative is being calculated.
Outlines
📚 Introduction to Multi-variable Chain Rule
This paragraph introduces the concept of the chain rule in multi-variable calculus, typically covered in Calculus 3. It contrasts the single-variable chain rule with the multi-variable case, where functions are dependent on more than one variable. The paragraph explains the differential notation and how it is used in various calculus applications. The focus then shifts to the multi-variable chain rule, especially when intermediate variables are also functions of another variable, such as 't'. The formula for the differential 'dz/dt' is derived by considering differentials and partial derivatives, leading to a comprehensive understanding of how to compute the derivative of a function of multiple variables with respect to a single variable.
🔍 Applying the Chain Rule with Tree Diagrams
The second paragraph delves into the practical application of the chain rule using tree diagrams, which help visualize the process and determine the type of derivatives—ordinary or partial—required at each step. The paragraph provides a step-by-step guide on setting up a tree diagram for functions of multiple variables and explains how to identify the correct paths to compute the derivative with respect to a given variable. It also illustrates how to convert the final expression into terms of the variable of interest, using an example where 'z' depends on 'x' and 'y', which in turn depend on 't'. The process of distributing and simplifying the resulting expression is also covered.
🌐 Complex Functions with Multiple Dependent Variables
This paragraph extends the concept to cases where 'z' is a function of both 'x' and 'y', and both 'x' and 'y' are functions of two variables, 's' and 't'. It discusses the setup of a more complex tree diagram to handle such scenarios and the importance of identifying all paths leading to the derivative with respect to a specific variable. The paragraph provides an example calculation for 'dz/dt', emphasizing the need to express the final answer in terms of the variables present in the bottom row of the tree diagram, which in this case are 's' and 't'.
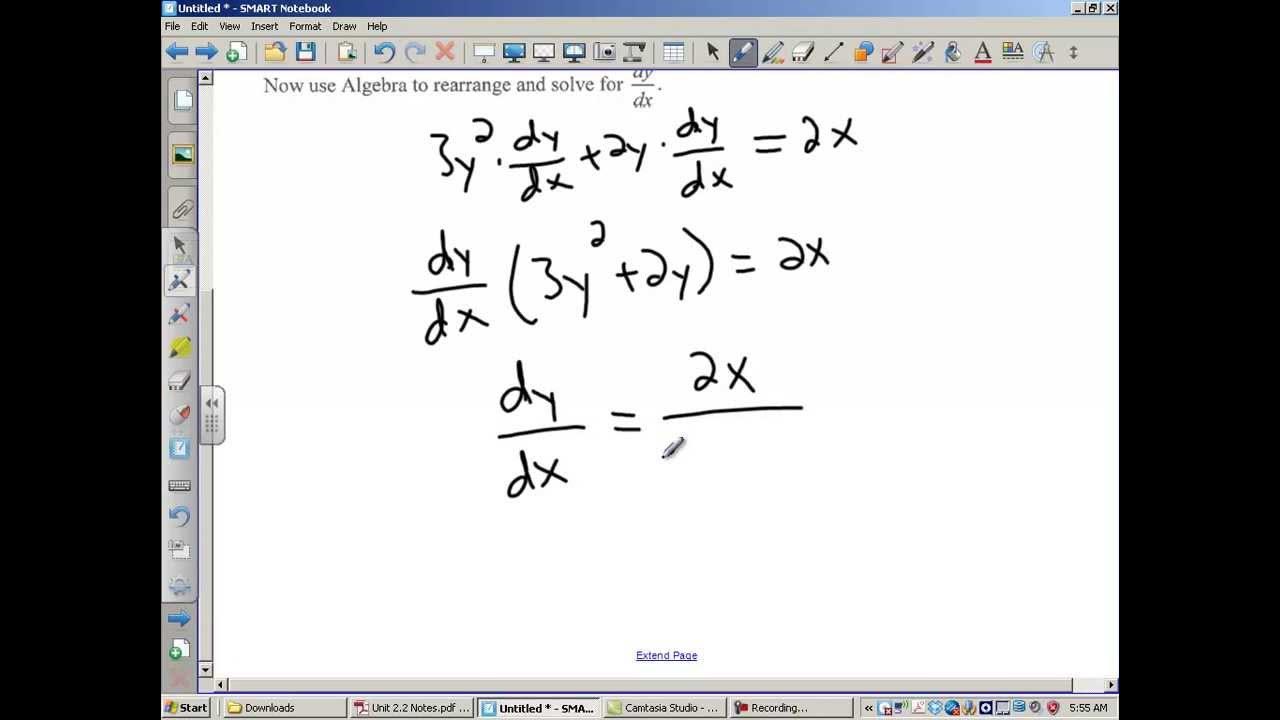
📝 Calculating Partial Derivatives in Advanced Scenarios
The final paragraph presents an advanced example of calculating partial derivatives when 'z' is a function of 'x' and 'y', and both 'x' and 'y' are functions of 's' and 't'. It demonstrates the process of finding both '∂z/∂s' and '∂z/∂t', using the previously derived derivatives and the tree diagram to guide the calculation. The paragraph shows the conversion of intermediate results into terms of 's' and 't', and the simplification of the final expression. It also touches on the possibility of further factoring the result for clarity, depending on the preference of the individual or instructor.
Mindmap
Keywords
💡Chain Rule
💡Multi-Variable Calculus
💡Partial Derivative
💡Differentials
💡Ordinary Derivative
💡Tree Diagram
💡Composite Function
💡Function of a Variable
💡Linear Approximation
💡Separable Differential Equations
Highlights
Introduction to the chain rule for multi-variable calculus, typically seen in Calculus 3.
Explanation of the differential 'dy' in the context of functions of one variable and its applications.
Introduction of the total differential 'dz' for functions of multiple variables, such as z being a function of x and y.
The multi-variable chain rule is discussed, especially when variables are functions of another variable, like t.
Derivation of the formula for 'dz/dt' using differentials and partial derivatives.
Use of tree diagrams to visualize and understand the chain rule for functions of multiple variables.
Differentiation between ordinary and partial derivatives based on the structure of the tree diagram.
Example calculation of 'dz/dt' for a function z = x^3 + y^3 with x and y as functions of t.
Conversion of variables to a common denominator, such as t, to express the derivative in terms of the independent variable.
Demonstration of a case where both x and y are functions of two variables, s and t.
Calculation of partial derivatives 'dz/ds' and 'dz/dt' for a function z(x, y) with x and y functions of s and t.
Restatement of derivatives in terms of the lowest level variables in the tree diagram for clarity.
Factoring of the resulting expressions for a cleaner and potentially simplified form.
Emphasis on the importance of correctly identifying the type of derivative (ordinary or partial) based on the tree diagram.
Highlighting the practical application of the multi-variable chain rule in various mathematical problems.
Final example illustrating the process of calculating partial derivatives in a complex scenario with multiple variables.
Conclusion summarizing the importance of the multi-variable chain rule and its applications in advanced calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: