Understand Calculus In 10 Minutes – Part 2 Derivatives and Rate of Change
TLDRIn this educational video, John, founder of Taba class math and an experienced math teacher, dives into the applications of derivatives and related rates of change in calculus. Focusing on a classic problem involving the rate at which the height of fluid in a cylinder decreases as the fluid is pumped out, John explains the concept of related rates and demonstrates how to solve such problems step-by-step. He emphasizes the importance of understanding units of measurement and the relationship between volume and height in cylinders, offering insights into calculus' foundational concepts and encouraging viewers to persevere through the challenges of learning calculus.
Takeaways
- 📚 John, founder of Taba class math and a math teacher, highlights the importance of understanding derivatives and related rates of change in calculus.
- 🔮 Recommends the book 'The Humongous Book of Calculus Problems' for calculus students, emphasizing its step-by-step solutions to over a thousand problems.
- 🧩 Uses a classic calculus problem involving a cylinder and fluid volume changes to explain related rates of change and the application of derivatives.
- 📈 Explains how the rate at which fluid is removed from a cylinder (DV/DT) affects the height of the fluid level (DH/DT), introducing a real-world application of calculus.
- 📝 Emphasizes the need to consider units of measure in calculus problems, illustrating with liters and cubic meters in the context of volume change.
- 📊 Demonstrates the calculation process by relating the volume of a cylinder (V) to its height (H), using the formula V = 1000πr^2H to account for units of measure.
- 📉 Breaks down the differentiation process with respect to time (T), showcasing how to derive the rate of height change (DH/DT) from the volume change rate (DV/DT).
- 🛠 Highlights the importance of conversion factors in calculus, using meters and liters as an example to maintain consistency in units throughout calculations.
- 💡 Provides insights into how the radius of a cylinder impacts the rate at which the fluid level drops, offering two examples to visualize the concept.
- 📱 Encourages viewers to subscribe to his YouTube channel for more math tutorials and expresses gratitude for the support on his calculus videos.
Q & A
What is the main focus of the video?
-The main focus of the video is on applications of derivatives and related rates of change in calculus, specifically aimed at helping calculus students understand these fundamental concepts through a classic problem involving fluid levels in a cylinder.
Who is the target audience for the video?
-The target audience for the video is calculus students, likely at the college level, who are seeking to learn or deepen their understanding of derivatives and related rates of change.
What example is used to explain the concept of related rates of change?
-The example used to explain the concept of related rates of change involves a cylinder with fluid being removed at a certain rate, and the problem is to find how fast the fluid level drops as the volume is pumped out.
Why is the DV/DT described as negative in the calculus problem?
-DV/DT is described as negative because fluid is being removed from the cylinder, indicating a decrease in volume over time.
What is the significance of using meters and liters in the problem?
-The significance of using meters and liters is to maintain consistency in units of measure, particularly because the rate of fluid removal is given in liters per minute. A conversion factor is necessary to align the units used for volume (liters) with those used for the dimensions of the cylinder (meters).
How is the relationship between volume, radius, and height of the cylinder represented in the calculus problem?
-The relationship is represented by modifying the standard formula for the volume of a cylinder (V=πr²h) to account for units of measure, resulting in a formula that incorporates a conversion factor to relate volume in liters with radius and height in meters.
What is the purpose of the 'Humongous Book of Calculus Problems' recommended in the video?
-The 'Humongous Book of Calculus Problems' is recommended as a resource for calculus students to assist them in practicing and solving a wide variety of calculus problems, helping to deepen their understanding through step-by-step solutions in easy-to-understand language.
What does DH/DT represent in the context of the calculus problem?
-DH/DT represents the rate of change of the height of the fluid in the cylinder with respect to time, indicating how fast the fluid level is dropping as volume is being removed.
How do the dimensions of the cylinder affect the rate at which the fluid level drops?
-The dimensions of the cylinder, specifically the radius, significantly affect the rate at which the fluid level drops. A cylinder with a smaller radius will have its fluid level drop faster compared to a wider cylinder, assuming the same rate of fluid removal.
What advice is given to students facing challenges in their calculus courses?
-The video advises students not to give up when faced with challenges in their calculus courses, emphasizing that perseverance and hard work will eventually lead to understanding, despite the abstract and complex nature of calculus.
Outlines
📚 Introduction to Derivatives and Related Rates
The video begins with an introduction to the topic of derivatives and related rates of change, aimed at calculus students. The speaker, John, shares his background as a math teacher and his experience with creating educational content on YouTube. He recommends a book called 'The Humongous Book of Calculus Problems' for those looking to deepen their understanding of calculus. John sets the stage for a classic calculus problem involving a cylinder and the rate at which fluid levels drop when the fluid is being removed.
🧮 The Classic Calculus Problem
John presents a specific problem related to the rate of change of a fluid's height in a cylinder as it is being pumped out. The problem involves a cylinder with fluid being removed at a rate of 3,000 liters per minute, and the goal is to find out how fast the fluid level drops. He explains the need to relate the volume and height of the cylinder using calculus, specifically the first derivative, to solve this related rates of change problem.
📐 Setting Up the Equation
John discusses the importance of setting up the correct equation to relate the volume (V) and height (H) of the cylinder. He points out that the volume of the cylinder is given by the formula πR^2H, but adjustments must be made to account for the units of measurement, specifically converting from cubic meters to liters. He emphasizes the importance of using the correct conversion factors to ensure the units are consistent throughout the calculation.
🔄 Differentiating with Respect to Time
John explains the process of differentiating both sides of the volume-height equation with respect to time (T) to find the rate of change of the height (dh/dt). He clarifies that the radius (R) is constant in this scenario and proceeds to differentiate the equation, leading to an expression for dh/dt. The speaker then demonstrates how to solve for dh/dt by substituting the known values and simplifying the equation.
📊 Applying the Formula to Different Cylinders
John applies the derived formula to two different scenarios involving cylinders with radii of one meter and ten meters. He calculates the rate of change of the fluid level (dh/dt) for each cylinder and discusses the implications of the results. The smaller cylinder shows a faster drop in fluid level (95 centimeters per minute), while the larger cylinder has a much slower drop (less than one centimeter per minute). This illustrates the impact of cylinder size on the rate of fluid level change.
🌟 Wrapping Up and Encouragement
In the conclusion, John reflects on the power and applications of calculus, encouraging viewers to persevere through the challenges of learning it. He reiterates the importance of not giving up and continuing to work hard, as understanding calculus can lead to a deeper appreciation of its real-world applications. John thanks the viewers for their time and wishes them success in their mathematical endeavors.
Mindmap
Keywords
💡Derivatives
💡Related rates of change
💡Calculus problem
💡Volume
💡Height
💡Cylinder
💡Conversion factors
💡Rate of change
💡First derivative
💡Unit of measure
Highlights
Introduction to the importance of understanding derivatives and related rates of change in calculus.
John, a math teacher with a strong background in mathematics, introduces the topic and his educational work.
Recommendation of 'The Humongous Book of Calculus Problems' as a helpful resource for calculus students.
Explanation of a classic calculus problem involving a cylinder and fluid dynamics to illustrate related rates of change.
Discussion on the impact of cylinder dimensions on the rate of fluid level drop.
Introduction to the concept of related rates of change using a practical problem.
Explanation of the relationship between volume removal rate and the change in fluid height.
Overview of calculus notation for rates of change, emphasizing the importance of derivatives.
Detailed explanation of setting up and solving a calculus problem involving fluid dynamics.
Emphasis on the significance of units of measure in calculus problems, specifically in relation to volume and rate.
Introduction to converting units of measure to align with the problem's given data for accurate calculus application.
Step-by-step breakdown of differentiating both sides of an equation with respect to time to solve for the rate of height change.
Application of calculus to solve for how fast the fluid level drops in a cylinder given a specific volume removal rate.
Comparison of fluid level drop rates in cylinders with different radii to illustrate the practical application of calculus.
Final thoughts on the power and utility of calculus in solving real-world problems and encouragement for students facing challenges in learning calculus.
Transcripts
Browse More Related Video

Algebra vs. Calculus – What’s The Difference?
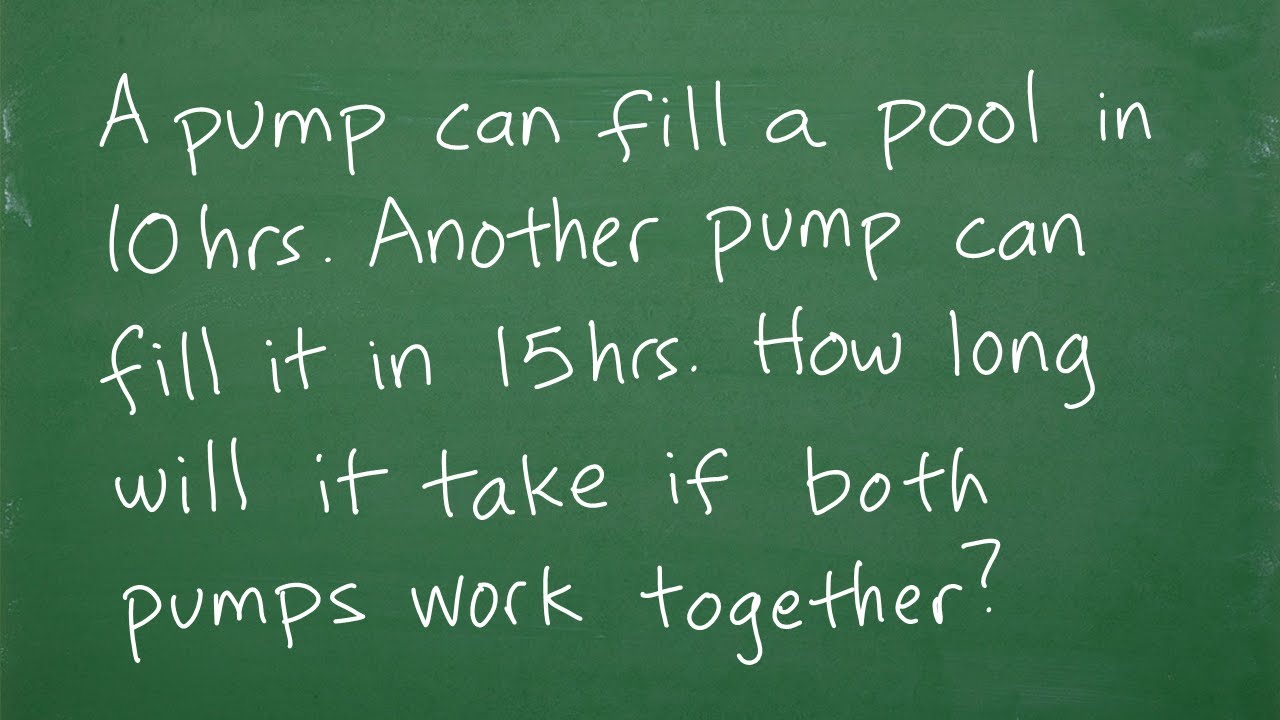
A pump can fill a pool in 10hrs. Another pump can fill it in 15hrs. Both pumps together will take?

Find the Derivative Using The PRODUCT RULE (Calculus Basics)

Math1325 Lecture 11-4 - Related Rates

Lesson 7 - Related Rates Problems in Calculus (Calculus 1 Tutor)

Related Rates Cone Example (Calculus)
5.0 / 5 (0 votes)
Thanks for rating: