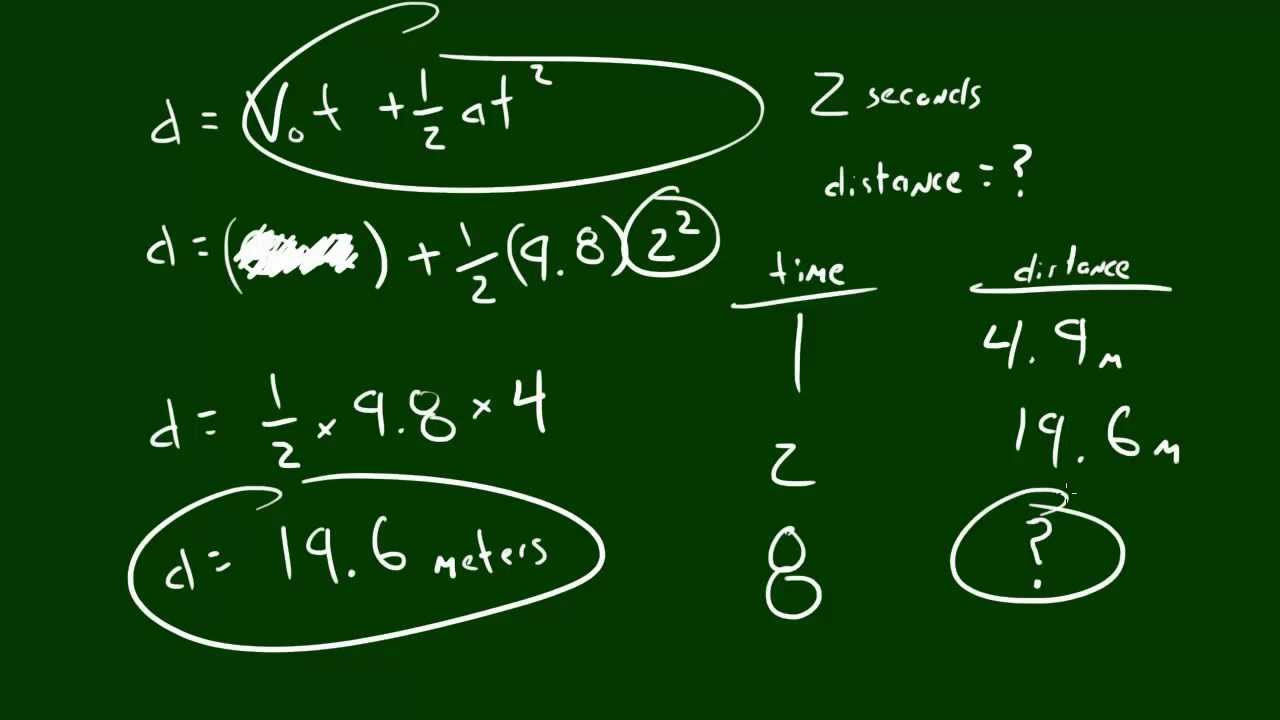Free Fall Problems
TLDRThe video script delves into the physics of free fall, exploring three distinct scenarios: dropping an object from a height, throwing an object upwards, and throwing it downwards. It employs kinematic equations to calculate the object's position, velocity, and time taken in each case, with a focus on the constant acceleration due to gravity (9.8 m/s^2). The tutorial provides step-by-step solutions, emphasizing the importance of vector direction and algebraic manipulation to arrive at accurate results.
Takeaways
- 📚 The script discusses three types of free fall physics problems: dropping an object from rest, throwing an object upwards, and throwing an object downwards.
- 🌟 Kinematic equations are essential for analyzing motion, specifically the equations relating final velocity, initial velocity, acceleration, time, and displacement.
- 🔢 For free fall problems, acceleration is considered uniform and is represented by 'g' (9.8 m/s²), directed downwards as the negative direction.
- 🏢 The first problem involves dropping an object from a height and analyzing its position and velocity as a function of time using the appropriate kinematic equations.
- 🏆 The second problem examines the motion of an object thrown upwards, focusing on maximum height reached, time to reach the top, and total flight time.
- 🎯 The third problem looks at an object thrown downwards, calculating the time it takes to reach the ground and its velocity upon impact.
- 📈 The script provides a step-by-step approach to solving these problems, emphasizing the importance of understanding the direction of motion and applying vector quantities correctly.
- 🤔 The script encourages viewers to practice problem-solving skills and engage with the content by subscribing, liking, and commenting on the video.
- 📊 The video uses examples and simplifications to illustrate the application of kinematic equations, such as neglecting the initial velocity in the case of an object dropped from rest.
- 🌐 The script emphasizes the importance of the vector nature of acceleration and the convention of defining positive and negative directions for the problems.
- 🔍 The analysis of each problem involves identifying the correct kinematic equation to use based on the information given and the unknowns to be solved for.
- 🎓 The tutorial serves as a comprehensive guide for understanding and solving free fall problems, highlighting the practical application of physics concepts.
Q & A
What are the three types of free fall problems discussed in the video?
-The three types of free fall problems discussed are: 1) Dropping an object from a height and analyzing its position and velocity as a function of time, 2) Throwing an object up in the air and analyzing its motion until it reaches its maximum height and falls back down, and 3) Throwing an object down from a height and analyzing the time it takes to reach the bottom.
What are the kinematic equations used to solve free fall problems?
-The three kinematic equations used to solve free fall problems are: 1) Final velocity (v) equals initial velocity (u) plus acceleration (a) times time (t), 2) Displacement (s) equals initial velocity (u) times time (t) plus one-half the acceleration (a) multiplied by time (t) squared, and 3) Final velocity (v) squared equals initial velocity (u) squared plus two times the acceleration (a) multiplied by the displacement (s).
What is the value of acceleration due to gravity (g) on the surface of the Earth?
-The value of acceleration due to gravity (g) on the surface of the Earth is 9.8 meters per second squared.
How is the acceleration due to gravity (g) represented in the free fall equations?
-In the free fall equations, the acceleration (a) is represented as minus the acceleration due to gravity (-g), indicating that the direction of acceleration is downward and has a value of -9.8 meters per second squared.
What is the initial velocity of an object when it is dropped from rest?
-When an object is dropped from rest, its initial velocity (u) is zero meters per second.
How is the time taken for an object to fall from a height of 7 meters calculated?
-The time taken for an object to fall from a height of 7 meters is calculated using the equation: s = ut - (1/2)gt^2, where s is the displacement (7 meters), u is the initial velocity (0 m/s), g is the acceleration due to gravity (9.8 m/s^2), and t is the time. Solving for t gives approximately 1.2 seconds.
What is the final velocity of an object just before it hits the ground after falling from a height of 7 meters?
-The final velocity of an object just before it hits the ground after falling from a height of 7 meters is calculated using the equation: v = u - gt, where v is the final velocity, u is the initial velocity (0 m/s), g is the acceleration due to gravity (9.8 m/s^2), and t is the time (1.2 seconds). The result is approximately -11.7 meters per second, indicating a downward velocity.
How long does it take for an object thrown upwards with an initial velocity of 6 m/s to reach its maximum height?
-To find the time it takes for an object thrown upwards with an initial velocity of 6 m/s to reach its maximum height, we use the equation: v = u - gt, where v is the final velocity (0 m/s at the top), u is the initial velocity (6 m/s), g is the acceleration due to gravity (9.8 m/s^2), and t is the time. Solving for t gives approximately 0.61 seconds.
What is the maximum height reached by an object thrown upwards with an initial velocity of 6 m/s?
-The maximum height reached by an object thrown upwards with an initial velocity of 6 m/s is calculated using the equation: s = ut - (1/2)gt^2, where s is the displacement, u is the initial velocity (6 m/s), g is the acceleration due to gravity (9.8 m/s^2), and t is the time to reach the top (0.61 seconds). The object reaches a maximum height of approximately 7.84 meters above the ground.
How is the total flight time of an object thrown upwards calculated?
-The total flight time of an object thrown upwards is calculated by determining the time to reach the maximum height and the time to fall back down from that maximum height. It is given by solving the quadratic equation derived from the displacement equation: s = ut - (1/2)gt^2, where s is the total displacement (negative of the initial height), u is the initial velocity, g is the acceleration due to gravity, and t is the time. The positive solution of this equation gives the total flight time.
What is the time taken for an object to fall 7 meters when thrown downwards with an initial velocity of 8 m/s?
-The time taken for an object to fall 7 meters when thrown downwards with an initial velocity of 8 m/s is calculated using the equation: s = ut - (1/2)gt^2, where s is the displacement (negative of 7 meters), u is the initial velocity (-8 m/s, considering the downward direction as negative), g is the acceleration due to gravity (9.8 m/s^2), and t is the time. Solving for t gives approximately 0.63 seconds.
What is the final velocity of an object just before it hits the ground after being thrown downwards with an initial velocity of 8 m/s?
-The final velocity of an object just before it hits the ground after being thrown downwards with an initial velocity of 8 m/s is calculated using the equation: v = u - gt, where v is the final velocity, u is the initial velocity (-8 m/s), g is the acceleration due to gravity (9.8 m/s^2), and t is the time (0.63 seconds). The result is approximately -14.2 meters per second, indicating a downward velocity of 14.2 meters per second.
Outlines
📚 Introduction to Free Fall Problems
The video begins with an introduction to free fall physics problems, outlining three different scenarios that will be analyzed. The first scenario involves dropping an object from a building and examining its position and velocity over time. The second scenario complicates the problem by throwing the object upwards, requiring analysis of its motion until it reaches maximum height and falls back down. The third scenario involves throwing the object downwards, which should take less time to reach the bottom. The video emphasizes the importance of understanding kinematic equations and their application to solve these free fall problems. The speaker also encourages viewers to support the channel and engage with the content by leaving comments and questions.
🔢 Kinematic Equations and Problem Solving
This paragraph delves into the kinematic equations necessary for solving free fall problems. The speaker introduces three fundamental equations for 1D motion with uniform acceleration. These equations relate final velocity, initial velocity, acceleration, time, and displacement. The speaker then adapts these equations specifically for free fall by incorporating the acceleration due to gravity (-g). The equations are as follows: final velocity equals initial velocity minus the product of g and time, displacement equals initial velocity times time minus half the product of g and time squared, and the square of the final velocity equals the square of the initial velocity minus twice the product of displacement and g. The speaker applies these equations to the first free fall scenario, where an object is dropped from a height, to determine the time it takes to fall and its final velocity.
📈 Analysis of Dropped Object's Motion
The speaker continues with the analysis of the dropped object, focusing on the object's motion, velocity, and time taken to fall from a height of seven meters. The paragraph explains how to use the second kinematic equation to calculate the time it takes for the object to hit the ground, given the initial velocity is zero and the acceleration is due to gravity. The speaker also explains how to determine the object's final velocity just before impact using the first kinematic equation. Additionally, the speaker explores the application of the third equation to confirm the result, emphasizing the vector nature of velocity and the importance of considering direction (downward being negative).
🚀 Throwing Object Up and Finding Maximum Height
This paragraph discusses the scenario of throwing an object upwards from a height of seven meters with an initial velocity of six meters per second. The speaker highlights the importance of understanding that at the maximum height, the vertical velocity is zero. The speaker uses the first kinematic equation to find the time it takes to reach the maximum height and then applies either the second or third equation to calculate the maximum height. The paragraph also covers how to find the speed of the object just before it hits the ground using the third kinematic equation, emphasizing the need to consider the total displacement for the entire motion, from the initial height to the ground.
📉 Time and Velocity Analysis for Object Thrown Downward
The final paragraph examines the scenario of throwing an object downward from a height of seven meters with an initial velocity of eight meters per second. The speaker explains how to use the second kinematic equation to calculate the time it takes for the object to fall seven meters. The speaker also discusses two methods for finding the object's velocity just before it hits the ground, using both the first and third kinematic equations. The paragraph concludes with a reminder to be careful with algebraic manipulation to ensure accurate results. The speaker wraps up the video tutorial by encouraging viewers to practice these problems and appreciates their engagement with the content.
Mindmap
Keywords
💡Free Fall
💡Kinematic Equations
💡Acceleration due to Gravity (g)
💡Displacement
💡Initial Velocity
💡Final Velocity
💡Vector Quantity
💡Maximum Height
💡Total Flight Time
💡Throwing Down
Highlights
Introduction to free fall problems and the three types of problems that will be analyzed.
Explanation of the kinematic equations and their application to free fall problems, including the importance of considering the direction of acceleration.
Discussion of the first problem, which involves dropping an object from a height and analyzing its position and velocity as a function of time.
Solution to the first problem using the appropriate kinematic equation and the concept of displacement.
Calculation of the time it takes for the ball to fall a distance of 7 meters using the derived equation.
Determination of the final speed of the ball just before it hits the ground using the first kinematic equation.
Application of the third kinematic equation to confirm the final speed result and the importance of considering the vector nature of velocity.
Introduction to the second problem, which involves throwing an object upwards and analyzing its motion to find the time to reach the top, maximum height, and total flight time.
Explanation of the importance of the vertical velocity being zero at the top position and how it simplifies the problem.
Use of the first kinematic equation to find the time to reach the maximum height and the simplification due to the initial velocity being positive upwards.
Calculation of the maximum height using either the second or third kinematic equation and the concept of displacement.
Determination of the speed just before hitting the ground using the third kinematic equation and the total displacement of the motion.
Solution for the total flight time using the second kinematic equation and the transformation into a quadratic equation.
Introduction to the third problem, which involves throwing an object downwards and analyzing the time to drop and the final velocity.
Calculation of the time it takes to drop seven meters with an initial downward velocity using the second kinematic equation.
Determination of the final velocity just before hitting the ground using both the first and third kinematic equations and their consistency.
Conclusion of the free fall video tutorial and encouragement for viewers to practice solving these problems.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: