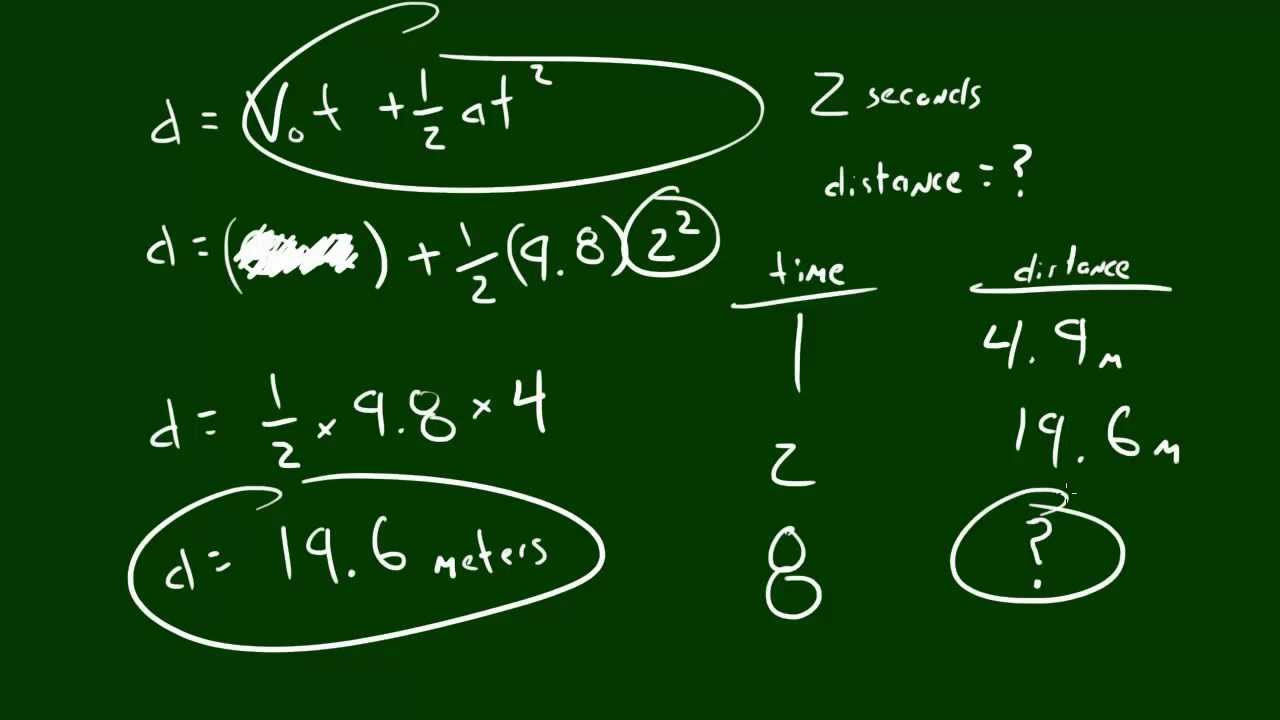AP Physics B Kinematics Presentation #32

The New Jersey Center for Teaching and Learning
26 Jun 201203:15
EducationalLearning
32 Likes 10 Comments

TLDRThis educational transcript explains the physics of a dropped ball falling 8 meters, using kinematic equations to calculate its final velocity. Starting with an initial velocity of 0 m/s and an acceleration due to gravity of 9.8 m/s², the formula \( v^2 = v_0^2 + 2a\Delta x \) is applied. After plugging in the values, the final velocity is determined to be 12.5 m/s, illustrating the principles of motion in a clear and concise manner.

Takeaways
  • 📉 The ball falls from a height of 8 meters to the ground.
  • 🚫 The initial velocity of the ball is 0 m/s because it is dropped.
  • 📉 The acceleration due to gravity (g) is 9.8 m/s², acting downwards.
  • 🔍 The problem involves solving for the final velocity (v) of the ball.
  • 📚 Three kinematic equations are presented: v = u + at, v² = u² + 2as, and x = ut + 1/2at².
  • 🎯 The chosen equation to solve for final velocity is v² = u² + 2as.
  • 🔢 The initial velocity (u) is substituted as 0 m/s in the equation.
  • 🔢 The acceleration (a) is substituted as 9.8 m/s², and the change in position (Δx) as -8 m.
  • 🔄 The negative sign in Δx is accounted for, making the result positive.
  • 🧮 The calculation involves squaring the acceleration and multiplying by the change in position, resulting in 156.25.
  • 📏 The square root of 156.25 is taken to find the final velocity, which is 12.5 m/s.
Q & A

  • What is the scenario described in the transcript?

    -The scenario involves a ball that is dropped from a certain height, resulting in a fall of 8 meters to the ground.

  • What is the initial velocity of the ball when it is dropped?

    -The initial velocity of the ball is 0 m/s, as it starts from rest.

  • What is the acceleration acting on the ball during its fall?

    -The acceleration acting on the ball is the gravitational acceleration, which is 9.8 m/s².

  • What is the final position of the ball after the fall?

    -The final position of the ball is at ground level, which is 0 meters in height from the starting point.

  • What kinematic equation is chosen to solve for the final velocity of the ball?

    -The chosen kinematic equation to solve for the final velocity is v^2 = v_0^2 + 2aΔx.

  • What is the change in position (Δx) of the ball during its fall?

    -The change in position (Δx) is 8 meters, as the ball falls from a height to the ground.

  • How is the final velocity calculated from the given equation?

    -The final velocity is calculated by taking the square root of the sum of the square of the initial velocity and twice the product of acceleration and change in position.

  • What is the mathematical operation performed to isolate the final velocity (v) in the equation?

    -The mathematical operation performed is taking the square root of both sides of the equation to isolate v.

  • What is the result of the calculation for the final velocity of the ball?

    -The final velocity of the ball is calculated to be 12.5 m/s.

  • Why do the negatives in the equation become positive when calculating the final velocity?

    -The negatives become positive because the ball is falling downwards, and the acceleration due to gravity is also in the downward direction, making the product of acceleration and change in position positive.

  • What is the significance of the negative sign in the change in position (Δx) in the equation?

    -The negative sign in Δx indicates the direction of the fall is downwards, which is the opposite of the positive direction typically used in calculations. However, since both the acceleration and the change in position are in the same direction, the result is positive.

Outlines
00:00
📉 Calculating Final Velocity of a Dropped Ball

This paragraph explains the physics problem of calculating the final velocity of a ball that has fallen 8 meters. The initial conditions are set: the ball is dropped, so the initial velocity is 0 m/s, and the acceleration due to gravity (g) is -9.8 m/s². The kinematic equation v^2 = v_0^2 + 2aΔx is chosen to solve for the final velocity (v). The process involves substituting the given values into the equation, simplifying, and taking the square root to find v. The calculation results in a final velocity of 12.5 m/s, which is derived from the equation v = √(0 + 2 * 9.8 * (-8)), where the negatives cancel out, leading to a positive result.

Mindmap
Keywords
💡Dropped Ball
A 'dropped ball' refers to an object, in this case a ball, that is released from rest and falls freely under the influence of gravity. In the video, the dropped ball is the subject of the physics problem, illustrating the concept of free fall motion. The ball falls 8 meters, and the video discusses how to calculate its final velocity using kinematic equations.
💡Final Velocity
The 'final velocity' is the speed at which an object is moving at the end of its motion. It is a key quantity in the script, as the problem presented involves calculating the ball's final velocity after falling 8 meters. The video uses kinematic equations to demonstrate how to find this velocity from the given initial conditions.
💡Change in Position (Delta X)
'Change in position' or 'Delta X' is the difference in an object's position from its starting point to its endpoint. In the context of the video, Delta X is the distance the ball falls, which is 8 meters. This term is crucial for applying the kinematic equations to find the final velocity.
💡Initial Velocity
The 'initial velocity' is the speed of an object at the beginning of its motion. In the script, the initial velocity of the dropped ball is specified as 0 m/s, indicating that it starts from rest. This information is essential for solving the kinematic equation for final velocity.
💡Acceleration (G)
'Acceleration' is the rate of change of velocity of an object. In the video, 'G' represents the acceleration due to gravity, which is 9.8 m/s². This constant acceleration is used in the kinematic equations to calculate the final velocity of the falling ball.
💡Kinematic Equations
Kinematic equations are formulas used in physics to relate an object's displacement, initial velocity, final velocity, acceleration, and time. The video script discusses three of these equations, ultimately choosing one to solve for the final velocity of the ball as it falls.
💡Square Root
The 'square root' is a mathematical operation that finds a number which, when multiplied by itself, gives a specified number. In the script, the square root is used to solve for the final velocity after rearranging the kinematic equation, showing the mathematical process involved in the calculation.
💡Free Fall Motion
'Free fall motion' describes the motion of an object when it is solely under the influence of gravity, starting from rest. The video's theme revolves around this concept, as it calculates the final velocity of a ball in free fall, using the principles of physics to solve the problem.
💡Displacement
In physics, 'displacement' refers to the change in position of an object. In the context of the video, displacement is the 8 meters the ball falls, which is a key piece of information used in the kinematic equations to find the final velocity.
💡Calculation
The 'calculation' in the video involves using the given values and kinematic equations to find the final velocity of the ball. It demonstrates the process of applying mathematical operations to solve a physics problem, which is central to the video's educational content.
💡Velocity
In the script, 'velocity' is the measure of an object's speed in a specific direction. The video focuses on calculating the final velocity of the ball, which is a fundamental concept in understanding the motion of objects under gravity.
Highlights

The problem involves calculating the final velocity of a ball dropped from a height of 8 meters.

The initial velocity of the ball is given as 0 m/s because it is dropped.

The acceleration due to gravity (g) is taken as 9.8 m/s^2.

The kinematic equation v^2 = v0^2 + 2aΔx is chosen to solve for the final velocity.

The initial velocity (v0) is substituted as 0 m/s in the kinematic equation.

The change in position (Δx) is given as -8 m, indicating the downward direction.

The equation simplifies to v^2 = 2aΔx due to the initial velocity being zero.

The square root of the equation is taken to isolate the final velocity (v).

The values are substituted into the equation: v = √(2 * 9.8 * -8).

The negative sign in the equation is resolved, resulting in a positive value.

The calculation simplifies to v = √(156.25).

The final velocity of the ball is determined to be 12.5 m/s.

The process involves basic physics principles and kinematic equations.

The problem demonstrates the application of the equation of motion for free fall.

The solution requires understanding the relationship between initial velocity, acceleration, and displacement.

The calculation is straightforward once the correct kinematic equation is chosen.

The final velocity is a critical parameter in various physics problems involving motion.

The problem-solving approach can be applied to other scenarios with constant acceleration.

The method highlights the importance of considering the direction of displacement in kinematic equations.

The solution process is a clear example of how to apply physics formulas to real-world problems.

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation #31

AP Physics B Kinematics Presentation #03

AP Physics B Kinematics Presentation #35

Kinematic Equations in One Dimension | Physics with Professor Matt Anderson | M2-04

Physics Lecture - 4 - Calculating Distance Traveled

AP Physics Workbook 1.J Vertrical Motion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsKinematicsVelocityAccelerationFree FallGravityMotion AnalysisEducationalScienceCalculation