Deriving Natural Logarithms!
TLDRThe video script provides an in-depth exploration of logarithms, focusing on their derivation and application in solving exponential equations. It begins by motivating the need for logarithms through the example of solving equations like 2^x = 8, and moves on to define logarithms as the inverse operation to exponentiation. The script then delves into the properties of natural logarithms (log base e), illustrating how they can be simplified using key relationships such as log(a*b) = log(a) + log(b), log(a/b) = log(a) - log(b), and log(a^b) = b*log(a). The importance of algebraic manipulation before differentiation is emphasized to avoid complex rules. The video continues with the application of the chain rule to derive functions involving natural logs, including examples with different algebraic structures. It concludes with the use of implicit differentiation to find equations of tangent lines for functions involving natural logs, highlighting the utility of logarithmic properties in calculus. The script is an excellent resource for those looking to understand the conceptual underpinnings and practical applications of logarithms in mathematical problem-solving.
Takeaways
- 📚 Logarithms are used to solve exponential equations, such as finding the power x in 2^x = 8.
- 🔑 The definition of a logarithm is log base B of Y equals x, which translates to B^x = Y.
- 🌱 Logarithms can be used with any base, but the focus is on the natural logarithm (base e), denoted as ln.
- 🔍 To find the value of a logarithm, you can translate the logarithmic equation back to its exponential form and solve for x.
- ➡️ The natural log and the exponential function with base e are inverse functions, meaning ln(e^x) = x and e^(ln(x)) = x.
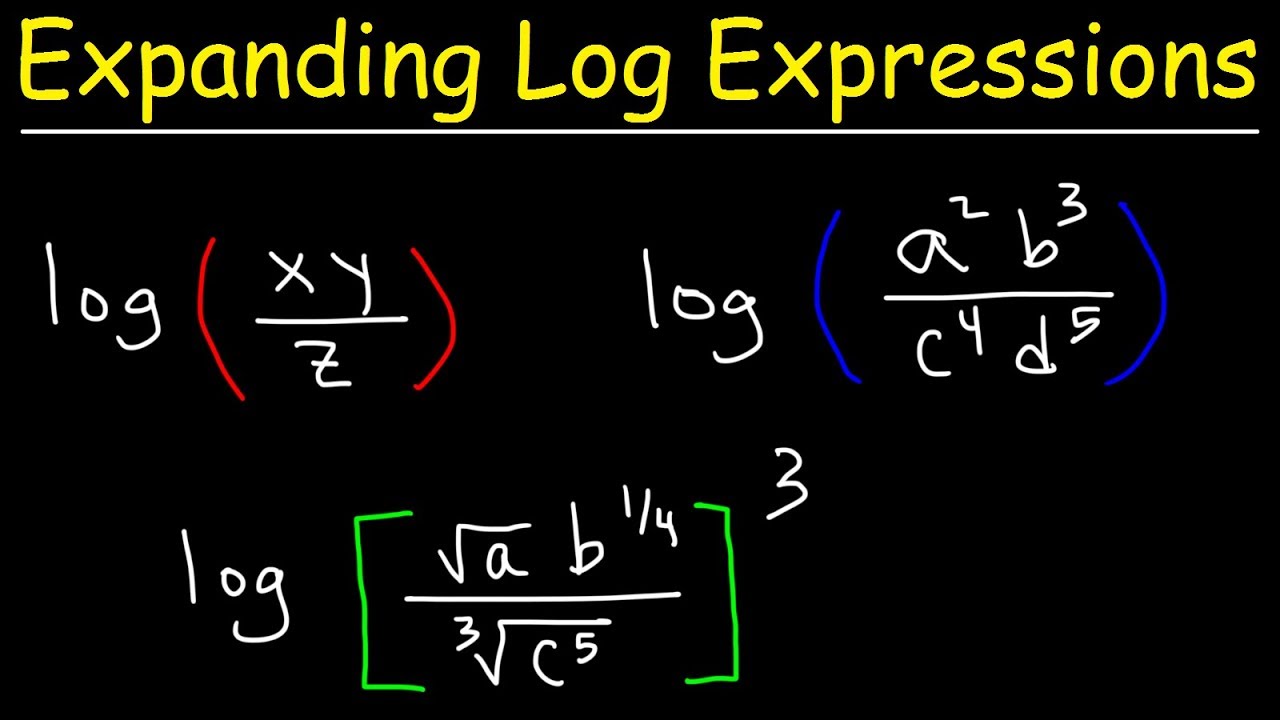
- ✅ Key logarithmic properties include: log(a*b) = log(a) + log(b), log(a/b) = log(a) - log(b), and log(a^b) = b * log(a).
- 📝 When simplifying logarithms, you can use these properties to change products inside the log to sums outside, quotients to differences, and powers to multiplications.
- 🔧 To derive the natural log of a function, use the chain rule: (d/dx) ln(g(x)) = (g'(x) / g(x)).
- 🧮 For more complex logarithmic expressions, break them down using the properties of logarithms before applying the derivative rules.
- 📈 When finding the equation of a tangent line to a logarithmic function, first find the derivative, then use the point-slope form of a line.
- 📉 Implicit differentiation is used when the equation is not explicitly solved for y, applying logarithmic properties and the chain rule to find dy/dx.
Q & A
What is the primary use of logarithms?
-Logarithms are primarily used to help solve exponential equations. They allow us to translate questions about exponential growth or decay into a more manageable form.
How is the logarithm defined mathematically?
-Logarithms are defined as log base B of Y equals X, which is the translation of B to the power of X equals Y. This allows us to convert between exponential and logarithmic forms.
What is the natural logarithm?
-The natural logarithm, often denoted as ln(X), is a special case of the logarithm where the base is the mathematical constant e (approximately equal to 2.71828). It is a commonly used logarithm and is abbreviated to simplify notation.
What is the relationship between the natural log and the exponential function e^x?
-The natural log and the exponential function e^x are inverse functions. This means that the natural log of e^x is equal to x, and e to the power of the natural log of X is also equal to X.
How can you simplify the logarithm log(x * y)?
-Using the logarithm properties, the expression log(x * y) can be simplified to log(x) + log(y). This is because multiplication inside the logarithm becomes addition outside the logarithm.
What is the derivative of the natural log of x with respect to x?
-The derivative of the natural log of x with respect to x is 1/x. This is derived using the chain rule, where the derivative of the inside (which is x) is divided by the original inside (which is also x).
How does the chain rule apply to the derivative of a natural log function?
-The chain rule states that the derivative of a composition of functions, such as the natural log of a function of x (ln(g(x))), is the derivative of the inside function times the derivative of the outside function. For ln(x), this simplifies to 1/x * g'(x).
What is the process to find the equation of a tangent line to a curve at a given point?
-To find the equation of a tangent line, first find the derivative of the function at the given point to get the slope of the tangent line. Then use the point-slope form of a line (y - y1 = m(x - x1)) and plug in the point and the derivative (slope) to find the equation of the tangent line.
How does implicit differentiation help in finding the equation of a tangent line?
-Implicit differentiation allows us to find the derivative of an equation that is not explicitly in the form y = f(x). By differentiating both sides of the equation with respect to x and isolating dy/dx, we can find the slope of the tangent line at any point on the curve without explicitly solving for y.
What is the significance of the natural log of e?
-The natural log of e (ln(e)) is equal to 1. This is a useful property because e is the base of the natural logarithm, and it simplifies calculations involving natural logs, especially when evaluating the derivative of ln(x) at x = e.
What is the general approach to simplifying complex logarithmic expressions before differentiation?
-The general approach involves using logarithm properties to simplify the expression. Multiplication inside a logarithm becomes addition outside, division becomes subtraction, and exponentiation becomes multiplication outside the logarithm. This simplification often makes differentiation easier.
Outlines
🧮 Introduction to Logarithms and Derivatives
The video begins with an introduction to logarithms, explaining their role in solving exponential equations. It illustrates how logarithms are derived from questions like solving for x in 2^x = 8, and how they are used to find values of x in more complex equations like 2^x = 10. The concept of logarithms as the inverse operation to exponentiation is introduced, with a focus on the natural logarithm (base e). The video also explains the translation of logarithmic expressions and their importance in mathematical problem-solving.
🔢 Key Relationships and Simplification Techniques
This paragraph delves into the fundamental relationships of natural logarithms, such as how ln(e^x) is equal to x and e^(ln(x)) equals x. The video emphasizes the utility of algebraic manipulation before differentiation to simplify expressions within logarithms. It covers how multiplication inside a logarithm translates to addition outside, division to subtraction, and powers to multiplication outside the logarithm. The paragraph also includes examples of simplifying complex logarithmic expressions using these relationships.
📚 Deriving Natural Logs and Applying the Chain Rule
The video moves on to the process of deriving natural logarithms. It introduces the rule that the derivative of the natural log of x is 1/x and extends this to more complex cases using the chain rule. Several examples are provided to demonstrate how to apply this rule to various functions involving natural logs, including those with multiplication, division, and powers. The importance of algebraic simplification before differentiation is reiterated for its efficiency.
🔁 Simplifying Expressions Using Logarithm Properties
The script focuses on simplifying logarithmic expressions by applying properties such as rewriting multiplication inside a logarithm as addition outside, and division as subtraction. It also covers how to handle powers inside a logarithm. The paragraph demonstrates how these properties can simplify the process of differentiation, especially when applying product, quotient, and chain rules.
🧵 Implicit Differentiation and Tangent Lines
This section introduces implicit differentiation and finding the equation of tangent lines involving natural logarithms. The video explains how to deal with x times y terms and how to use logarithmic properties to simplify the differentiation process. It also shows how to find the slope of a tangent line and derive the equation of the tangent line at a specific point on a graph defined by a function involving natural logs.
🎓 Summary and Final Thoughts on Logarithm Derivatives
The video concludes with a summary of the key points covered, emphasizing the origin of logarithms from solving exponential equations and their utility in simplifying complex expressions. It reiterates the logarithmic properties and the process of deriving natural logs, particularly using the chain rule for more complicated expressions. The presenter encourages viewers to practice with the new rules and offers help for any questions, wrapping up with well wishes.
Mindmap
Keywords
💡Logarithms
💡Natural Logarithm
💡Derivative
💡Chain Rule
💡Exponential Equations
💡Logarithmic Properties
💡Implicit Differentiation
💡Tangent Line
💡Product Rule
💡Quotient Rule
💡Exponential Functions
Highlights
Logarithms are used to solve exponential equations and come from the need to find the power x in equations like 2^x = 8.
Logarithms are defined as log base B of y equals x, which translates to B^x = y.
Natural logarithm, or log base e, is a special case of logarithm and is often denoted as ln.
The natural log of 1 is always 0, as any number to the power of 0 equals 1.
The natural log and e^x are inverse functions, meaning the natural log of e^x is x and vice versa.
Logarithmic properties allow multiplication inside the log to be rewritten as addition outside, and division as subtraction.
When simplifying logarithms, powers inside the log can be rewritten as multiplication outside.
Derivatives of natural logarithms follow the rule: if f(x) = ln(g(x)), then f'(x) = g'(x) / g(x).
Algebraic simplification before differentiation can often simplify the process and avoid more complicated rules.
The chain rule is essential for deriving more complex natural logarithm functions, such as ln(x^2 + 5x).
Implicit differentiation is used when the equation is not explicitly solved for y, such as in ln(x*y + 5x) = 30.
The equation of a tangent line can be found using the point-slope form and the derivative of the function at the point of interest.
The natural log of e is a special case that equals 1, simplifying many expressions involving ln(e).
The quotient rule is applied when differentiating expressions like ln(x/(x^3)) by considering it as a division.
When a power is outside of a logarithm, as in (ln(x))^4, the chain rule must be applied to differentiate it.
The derivative of a natural log involving a root or fractional power can be simplified by rewriting the root as a power and applying logarithmic properties.
The process of finding the equation of a tangent line involves finding the derivative of the function, evaluating it at a specific point, and using the point-slope form.
The natural log function has a wide range of applications in mathematics, including simplifying derivatives and solving exponential equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: