AP Physics B Kinematics Presentation #55

The New Jersey Center for Teaching and Learning
26 Jun 201203:19
EducationalLearning
32 Likes 10 Comments

TLDRThis script explores the concept of vector addition, emphasizing that the resultant vector is largest when vectors are aligned at zero degrees. By contrasting scenarios with angles of 0, 45, 90, and 180 degrees, the explanation demonstrates that misalignment reduces the magnitude of the resultant vector. The conclusion is clear: the maximum resultant vector occurs when vectors are in the same direction, debunking the idea that 90 or 180 degrees might yield a greater result.

Takeaways
  • πŸ“š The resultant of two vectors is the vector sum of their magnitudes and directions.
  • πŸ“ The largest resultant occurs when the angle between the two vectors is zero degrees.
  • 🧭 A vector pointing east with a magnitude of 7 meters and another pointing east with 3 meters results in a 10-meter resultant vector.
  • πŸ”„ If one vector is 180 degrees out of phase with the other, the resultant is smaller, sometimes less than the magnitude of one vector.
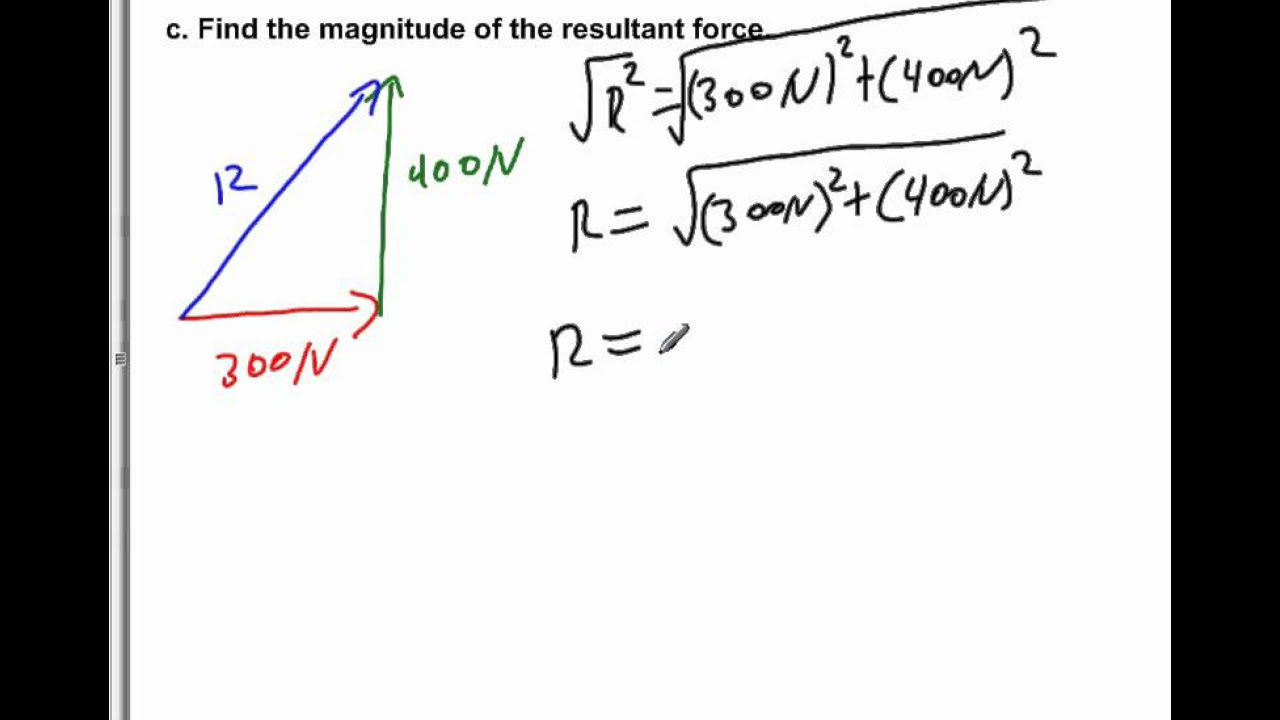
  • πŸ”’ The resultant of two vectors at a 90-degree angle is found using the Pythagorean theorem, resulting in a smaller magnitude than when they are aligned.
  • πŸ€” The script explores the effect of different angles (0, 45, 90, and 180 degrees) on the magnitude of the resultant vector.
  • πŸ“‰ At a 90-degree angle, the resultant vector is smaller than when vectors are aligned in the same direction.
  • πŸ“ˆ The magnitude of the resultant vector decreases as the angle between the two vectors increases from 0 to 180 degrees.
  • πŸ” The script uses examples with specific vector magnitudes to illustrate the principles of vector addition.
  • πŸ“ˆ The resultant vector is maximized when all components of the vectors are in the same direction, indicating a 0-degree angle.
  • 🎯 The conclusion is that a 0-degree angle between two vectors yields the largest possible resultant vector.
Q & A

  • What is the resultant of two vectors?

    -The resultant of two vectors is the vector that represents the combined effect of the two vectors when they are added together.

  • What is the angle between two vectors when their resultant is the largest?

    -The resultant of two vectors is the largest when the angle between them is zero degrees, meaning they are in the same direction.

  • Why is the resultant smaller when the angle between vectors is 180 degrees?

    -When the angle is 180 degrees, the vectors are in opposite directions, which results in a smaller resultant because they partially cancel each other out.

  • What is the effect of a 90-degree angle between two vectors on their resultant?

    -A 90-degree angle between two vectors results in a resultant that is smaller than if they were aligned in the same direction, due to the perpendicular nature of their addition.

  • How does a 45-degree angle affect the resultant of two vectors?

    -A 45-degree angle between two vectors results in a resultant that is not as large as when the vectors are aligned in the same direction, due to the diagonal nature of their addition.

  • What is the mathematical formula used to calculate the resultant of two vectors at a given angle?

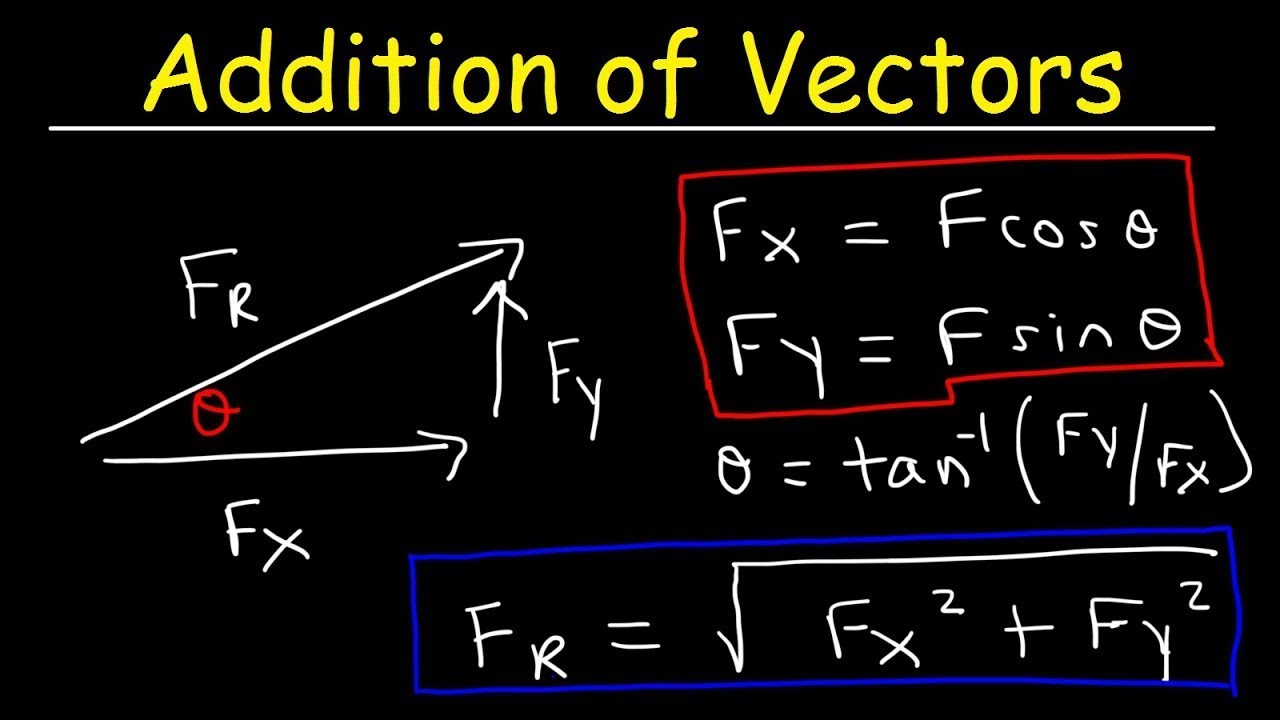
    -The formula for the magnitude of the resultant vector R when two vectors A and B are at an angle ΞΈ is \( R = \sqrt{A^2 + B^2 + 2AB\cos(\theta)} \).

  • Can the resultant of two vectors ever be greater than the sum of their magnitudes?

    -No, the resultant of two vectors cannot be greater than the sum of their individual magnitudes because the maximum resultant occurs when the vectors are aligned, which is simply the sum of their magnitudes.

  • What is the significance of the cosine function in the formula for the resultant of two vectors?

    -The cosine function in the formula represents the component of one vector that is in the direction of the other vector, affecting the magnitude of their resultant.

  • How can you visualize the addition of two vectors?

    -You can visualize the addition of two vectors by placing them head-to-tail and drawing the resultant vector from the tail of the first vector to the head of the second vector.

  • What happens to the resultant when the angle between two vectors decreases from 90 degrees to 0 degrees?

    -As the angle between two vectors decreases from 90 degrees to 0 degrees, the magnitude of their resultant increases, reaching its maximum when the vectors are aligned.

  • Why is it important to understand the concept of vector addition?

    -Understanding vector addition is important in various fields such as physics, engineering, and graphics, where forces, velocities, and other quantities are often represented as vectors.

Outlines
00:00
πŸ“š Vector Resultants at Different Angles

This paragraph discusses the concept of vector addition and how the resultant vector's magnitude varies with the angle between two vectors. It explains that the resultant is largest when vectors are aligned (0 degrees) and smallest when they are in opposite directions (180 degrees). The script uses examples with vectors of different magnitudes and angles, including 45 and 90 degrees, to illustrate the principles. The conclusion is that zero degrees yields the largest resultant vector, confirming option A as the correct answer to the initial question.

Mindmap
Keywords
πŸ’‘Resultant
The 'resultant' refers to the combined effect of two or more vectors, which can be thought of as the single vector that represents the net displacement or force in a given situation. In the video, the resultant is used to illustrate the effect of adding two vectors together, with the largest resultant occurring when the vectors are in the same direction, i.e., at zero degrees.
πŸ’‘Vectors
Vectors are quantities with both magnitude and direction, used to represent physical quantities such as force, velocity, or displacement. In the context of the video, vectors are used to demonstrate how different angles between them affect the magnitude of their resultant, with examples given for vectors pointing east and west.
πŸ’‘Angle
The 'angle' between two vectors is the measure of the space between their directions, typically measured in degrees. The video script explores how varying the angle between two vectors affects the magnitude of their resultant, showing that the resultant is maximized at zero degrees and minimized at 180 degrees.
πŸ’‘Magnitude
The 'magnitude' of a vector is its length or size, which represents the strength of the vector without considering its direction. The script explains that the magnitude of the resultant vector is greatest when the vectors are aligned in the same direction, thus maximizing the resultant's magnitude.
πŸ’‘Zero Degrees
A 'zero-degree' angle between two vectors indicates that they are pointing in exactly the same direction. The video uses this concept to show that the resultant vector is at its maximum magnitude when the angle is zero degrees, as all the components of the vectors add up directly.
πŸ’‘45 Degrees
A '45-degree' angle between two vectors suggests that they are at a diagonal to each other. The script demonstrates that even though the vectors contribute to the resultant, the magnitude of the resultant at a 45-degree angle is not as large as when the vectors are aligned at zero degrees.
πŸ’‘90 Degrees
A '90-degree' angle, or a right angle, between two vectors indicates that they are perpendicular to each other. The video explains that the resultant of two vectors at a 90-degree angle is less than the sum of their magnitudes, as they do not add directly to each other.
πŸ’‘180 Degrees
An '180-degree' angle between two vectors means they are directly opposite in direction. The script uses this to illustrate that the resultant of such vectors is minimal, as one vector's effect is almost completely negated by the other.
πŸ’‘Addition
In the context of vectors, 'addition' refers to the process of combining two or more vectors to find their resultant. The video script discusses the addition of vectors at various angles to demonstrate how the angle affects the outcome of the addition.
πŸ’‘Direction
The 'direction' of a vector is the orientation in which it points. The video emphasizes the importance of direction in determining the resultant vector, showing that the direction of the vectors plays a crucial role in the magnitude of the resultant.
πŸ’‘Displacement
While not explicitly mentioned in the script, 'displacement' is a physical quantity that can be represented by a vector, indicating the change in position of an object. The concept of displacement is implicitly discussed when the script talks about vectors pointing in different directions to represent movement.
Highlights

The resultant of two vectors is largest when the angle between them is zero degrees.

Drawing vectors helps to understand the concept of resultant vectors.

Example with one vector 7 meters to the east and another 3 meters to the east shows resultant of 10 meters at 0 degrees angle.

If one vector is 3 meters to the west, the resultant is reduced to 4 meters at 180 degrees angle.

180 degrees angle between vectors results in a smaller resultant than the individual vectors.

Two vectors at 90 degrees, 3 meters and 4 meters, have a resultant of 5 meters.

Resultant is greater when vectors are in the same direction compared to 90 degrees.

45 degrees angle between vectors, 3 meters and 4 meters, results in a smaller resultant than when aligned.

45 degrees does not create the largest resultant vector.

90 degrees angle reduces the overall value of the resultant vector.

Zero degrees alignment of vectors results in the largest possible resultant value.

The angle between vectors significantly impacts the magnitude of the resultant vector.

Vectors in opposite directions (180 degrees) yield a smaller resultant than individual vectors.

Vectors at 90 degrees do not produce the maximum resultant vector.

Vectors aligned in the same direction (0 degrees) give the maximum resultant vector.

The concept of resultant vectors is crucial in understanding vector addition.

Practical applications of resultant vectors include physics and engineering.

Transcripts

Browse More Related Video

How to use vectors to solve a word problem

AP Physics B Kinematics Presentation General Problems #08

AP Physics B Kinematics Presentation General Problems #07

Addition of Vectors By Means of Components - Physics

Vectors Full Topic -Physics

AP Physics B Kinematics Presentation #51

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Vector AnalysisAngles ImpactResultant VectorPhysics ConceptsMathematicsVector AdditionDirectional ForcesZero DegreesAngle EffectVector Magnitude