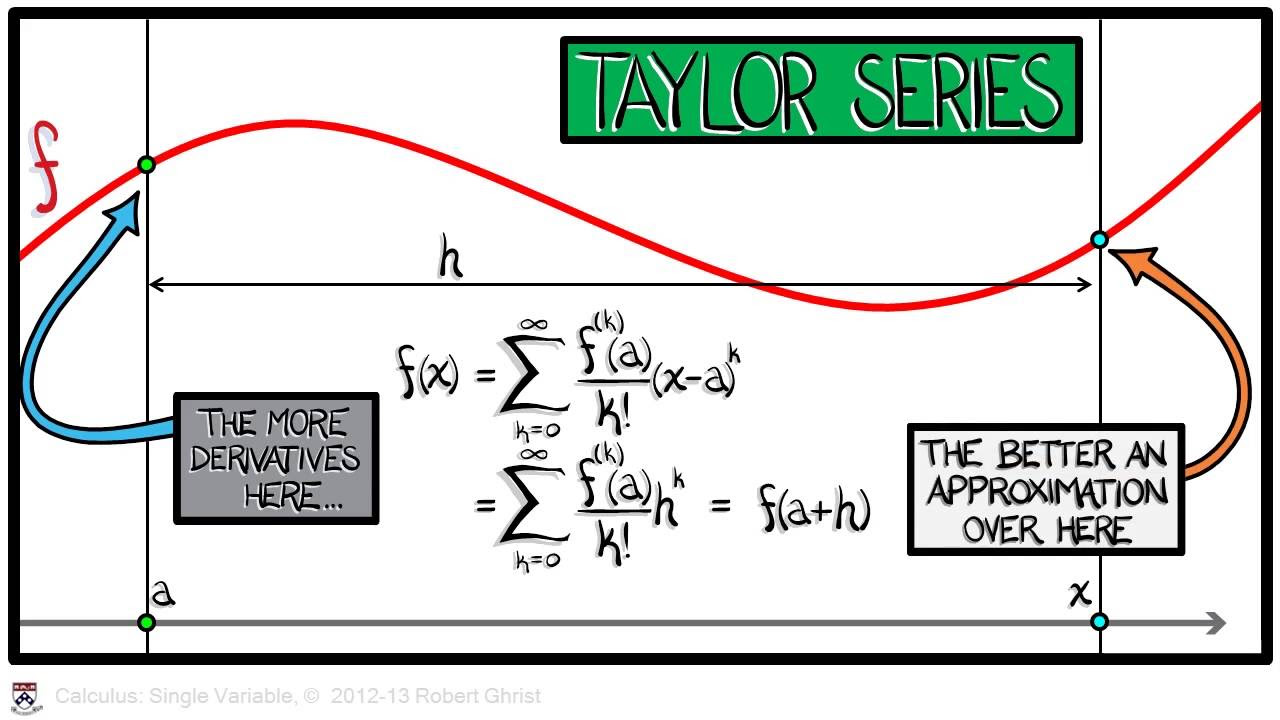
Calculus Chapter 5 Lecture 56 Approximation & Error
TLDRIn this calculus lecture, Professor Greist explores the intricacies of approximation and error within Taylor series and polynomial approximations. He delves into the convergence of the series 1/N^2 and its approximation to π^2/6, demonstrating the impact of summing varying numbers of terms. The lecture also covers error bounds for alternating series, the integral test, and Taylor expansions, providing methods to approximate values like 1/√e and log(2) with high precision. The professor emphasizes the importance of understanding and controlling error in mathematical approximations.
Takeaways
- 📚 The lecture discusses the concept of approximation and error in the context of calculus, particularly focusing on Taylor series and polynomial approximations.
- 🔍 It explains the convergence of the series 1/N^2 to a value related to π^2/6, and the difficulty in precisely determining this value, suggesting the use of approximations instead.
- 💻 The importance of computational tools in approximating values is highlighted, showing how adding more terms of a series can yield results closer to the true value.
- 🔢 The script provides an example of using the first 10, 20, 100, and 1000 terms of a series to approximate π^2/6, demonstrating the improvement in approximation with more terms.
- 📉 The concept of error in approximation is introduced, denoted as e_sub_n, and the idea of bounding this error to ensure the approximation is within an acceptable margin of error.
- 📈 The lecture explains the use of the alternating series test for series that meet certain criteria, providing a simple and useful way to bound the error in such series.
- 📚 An example of approximating 1/√e using an expansion of e^(-x) is given, illustrating how to determine the number of terms needed to achieve a specific error margin.
- 📐 The script delves into the use of the integral test for series that can be represented by an integrable function, offering a method to bound the error from below and above.
- 📘 The importance of understanding the error bounds associated with different types of series, such as alternating series and those that can be tested by integration, is emphasized.
- 🔑 The lecture introduces the Taylor expansion error bound, which provides a way to estimate the error in approximations when the function is smooth and expanded around x=0.
- 🔍 The script concludes by discussing the challenges of bounding errors when neither the alternating series test nor the integral test is applicable, suggesting the use of Taylor's theorem or logical reasoning as alternatives.
Q & A
What is the main topic of Professor Greist's lecture 56?
-The main topic of the lecture is approximation and error, focusing on how Taylor series and polynomial approximations work and the process of approximation.
Why is the sum of 1 over N squared significant in the lecture?
-The sum of 1 over N squared is significant because it is an example of an infinite series that converges, and it is used to approximate the value of PI squared over 6.
What is the claim about the sum of 1 over N squared in relation to PI squared over 6?
-The claim is that the sum of 1 over N squared converges to PI squared over 6, which is a deep mathematical result that cannot be easily derived.
How does Professor Greist suggest approximating the true value of PI squared over 6?
-Professor Greist suggests using a computer to sum up the terms of the series to get an approximation of PI squared over 6, and increasing the number of terms summed to improve the approximation.
What is the concept of error in the context of approximation?
-In the context of approximation, error refers to the difference between the approximation and the true value. It is denoted by e sub n and can be controlled or bounded but not computed exactly.
How does the alternating series test help in bounding the error of an approximation?
-The alternating series test provides a simple and useful way to get an upper bound on the error e sub n in absolute value, which is precisely a sub n plus 1, the next term in the series.
What is the goal when approximating 1 over the square root of E using the expansion for e to the X?
-The goal is to add up a finite number of terms from the expansion to get the error less than one one-thousandth, which requires finding a capital n such that a sub capital n plus 1 is less than 1/1000.
How does the integral test provide a bound for the error in an approximation?
-The integral test provides a natural lower and upper bound for the error by integrating the function a of X from n plus 1 to infinity, which gives a strict lower bound, and by sliding everything over by one unit to get an upper bound.
What is the general approach when you don't have an alternating series or an integral test for bounding the error?
-When you don't have an alternating series or an integral test, you can resort to the Taylor theorem for an error bound, which involves Taylor expansion and provides a more complex but potentially more precise error bound.
How does Professor Greist illustrate the use of the Taylor theorem for approximating the square root of e?
-Professor Greist illustrates the use of the Taylor theorem by showing that the error u sub n is less than some constant C over n plus 1 factorial times X to the n plus 1, where C bounds the n plus first derivative of e to the X for all values of X between 0 and 1/2.
What is the final advice given by Professor Greist regarding bounding errors in approximations?
-Professor Greist advises that bounding errors is inherently difficult, and if the Taylor theorem doesn't work and it's not an alternating series, one must think critically and use their judgment to find a suitable approach for bounding errors.
Outlines
📚 Introduction to Approximation and Error in Calculus
Professor Greist begins lecture 56 with an exploration of approximation and error in the context of calculus. He discusses the convergence of the sum of 1 over N squared and its relation to PI squared over 6. The professor uses computational examples to demonstrate how many terms are needed to approximate this value within a certain percentage of accuracy. He introduces the concept of error (denoted as e sub n) and how it can be bounded, especially in the case of alternating series, providing a simple and useful method for error estimation.
🔍 Error Bounds in Alternating Series and the Integral Test
The lecture continues with an in-depth look at error bounds in alternating series, using the approximation of 1 over the square root of E as an example. The professor explains how to determine the number of terms needed to achieve a specific error threshold. He then contrasts this with non-alternating series, introducing the integral test as a method for establishing error bounds. The professor illustrates how the integral test provides a natural lower and upper bound for the error, offering precise control over the approximation's accuracy.
📉 Advanced Error Bounds Using Taylor Expansion
In this segment, Professor Greist delves into the complexities of error bounds using Taylor expansion. He explains the general form of the error term in a Taylor series and how it can be bounded by a constant times a power of X over a factorial. The professor provides a stronger version of the error bound, which involves the n plus first derivative of the function at a point between 0 and X. He demonstrates how this can be used to approximate the square root of E and the arcsine of 1/10 with high precision, emphasizing the importance of understanding the behavior of the function's derivatives.
🎓 Conclusion and Reflection on Approximation Techniques
The final paragraph wraps up the lecture with a summary of the main topics covered, including the challenges and strategies for bounding errors in various mathematical series. The professor reflects on the importance of thinking critically when traditional methods like Taylor bounds or the integral test are not applicable. He concludes by highlighting the broader implications of these concepts in calculus and mathematics, encouraging students to continue exploring these ideas beyond the lecture.
Mindmap
Keywords
💡Calculus
💡Taylor Series
💡Approximation
💡Error
💡Alternating Series
💡Integral Test
💡Convergence
💡P-Series
💡Error Bound
💡Taylor Expansion
💡Derivative
Highlights
Introduction to Lecture 56 on approximation and error in the context of Taylor series and polynomial approximations.
Explanation of the convergence of the sum of 1 over N squared and its relation to PI squared over 6.
Demonstration of how many terms are needed to approximate PI squared over 6 within a certain decimal accuracy using a computer.
Discussion on the general inability to reach the true value due to the nature of limits and the concept of approximation error.
Introduction of the error term e sub n and its significance in bounding the approximation error.
The criteria for the alternating series test and its application in bounding the error of an approximation.
Application of the alternating series test to approximate 1 over the square root of E within one one-thousandth.
The challenge of approximating log of 2 using the alternating harmonic series and the number of terms required.
Introduction of the integral test and its use in providing a natural lower and upper bound for the error term in non-alternating series.
The use of the integral test to approximate PI squared over 6 within one one-thousandth and the number of terms needed.
Discussion on the limitations of the Taylor expansion for error bounding when the series is not alternating and does not meet the integral test criteria.
Introduction of the strong form of the Taylor theorem that provides a more explicit bound for the error term.
Application of the Taylor theorem to approximate the square root of E within 10 to the negative 10 and the method to determine the number of terms.
The process of estimating the arcsine of 1/10 within 10 to the negative 10 using the Taylor expansion and the challenges in bounding the error term.
The importance of critical thinking in bounding errors when standard methods like the Taylor theorem or alternating series test are not applicable.
Conclusion of the main topics of the course and a look ahead to broader ideas in calculus and mathematics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: