Calculus Chapter 1 Lecture 5 Convergence
TLDRIn this calculus lecture, Professor Greist delves into the intricacies of series convergence, highlighting the challenges of adding infinite terms. He introduces the geometric series, demonstrating its convergence to 2 with algebraic manipulation, and discusses its domain of convergence, emphasizing caution at the borders. The lecture further explores the Taylor series for functions like log(1+x) and arctan(x), noting their limited convergence domains. The binomial series is also examined, showcasing its utility with different values of alpha. The key takeaway is the importance of operating within the convergence domain for accurate mathematical manipulation.
Takeaways
- 📚 The lecture introduces the concept of convergence in calculus, emphasizing the importance of understanding the behavior of infinite series.
- 🔍 It highlights the limitations of Taylor series, such as the inability of polynomials to capture the complexities of functions like the logarithm at x=0.
- 🌐 The script explains the geometric series and its convergence to 2 when the sum of \( \sum_{k=0}^{\infty} \left(\frac{1}{2}\right)^k \) is considered.
- 📝 A general formula for the geometric series is provided: \( \sum_{k=0}^{\infty} x^k = \frac{1}{1-x} \) for \( |x| < 1 \).
- 🔄 The process of proving the convergence of a geometric series is demonstrated through algebraic manipulation, with caution advised for values of x outside the domain of convergence.
- ❗ The dangers of adding an infinite number of terms are discussed, with examples showing that the sum can diverge or be undefined for certain values of x.
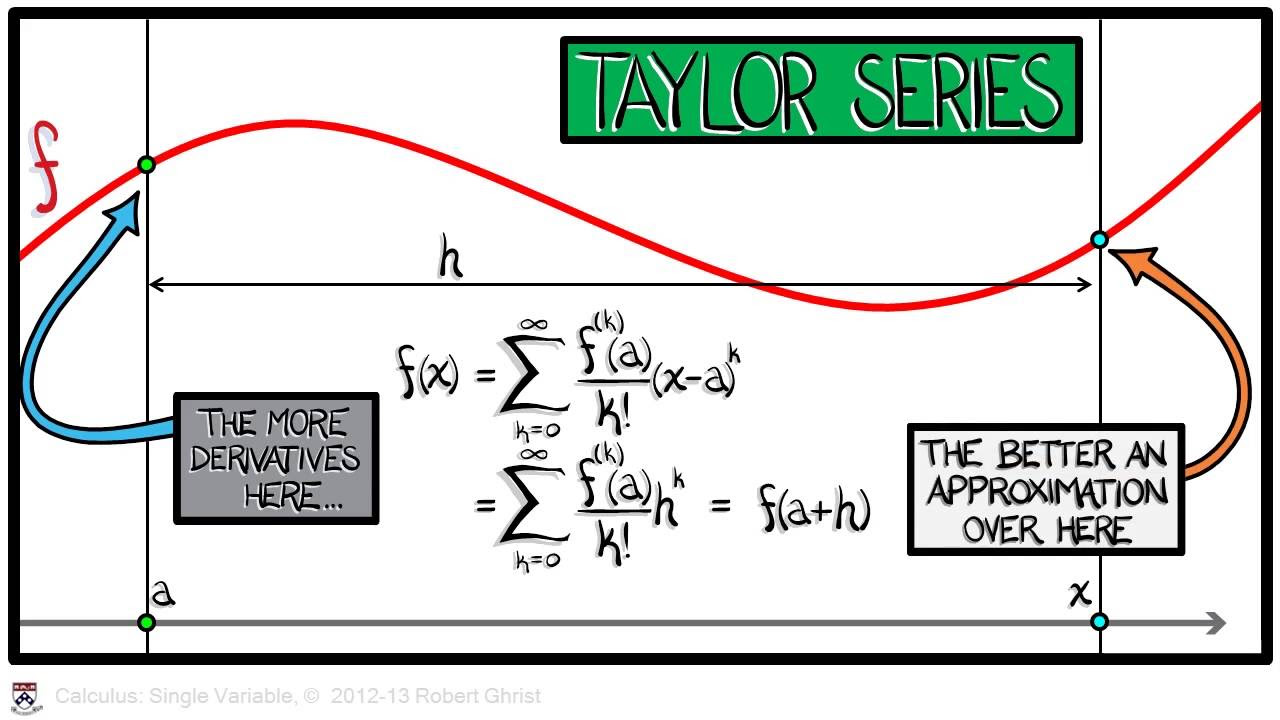
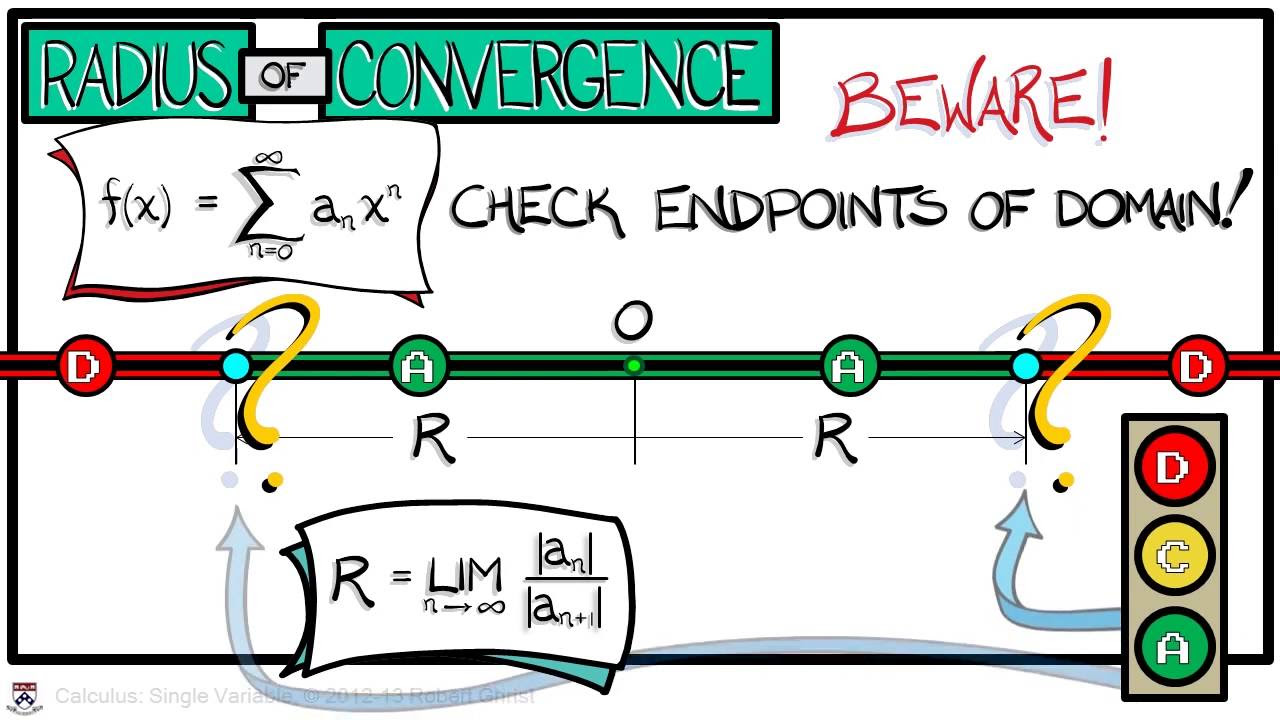
- 📉 The importance of the domain of convergence for Taylor series is stressed, noting that operations like differentiation and integration are valid within this domain.
- 📌 The script provides an example of deriving the Taylor series for \( \log(1 + x) \) using integration of the geometric series.
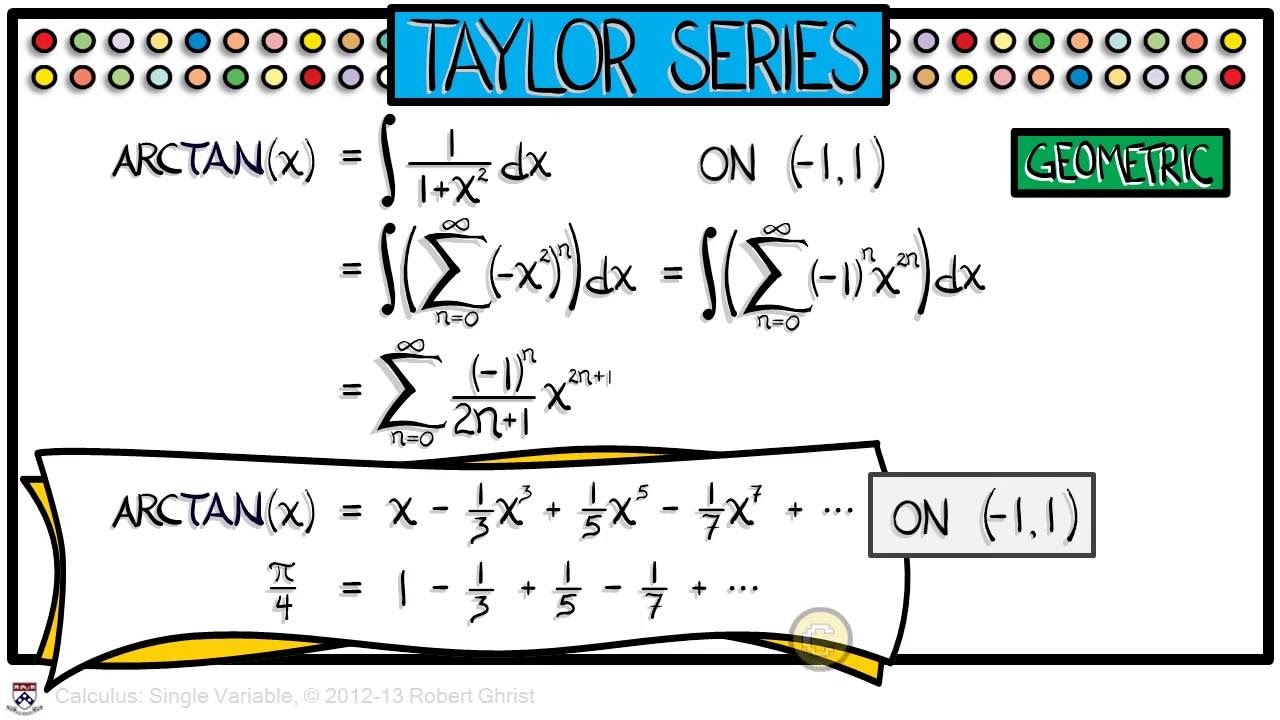
- 📈 The convergence domain for the Taylor series of \( \log(1 + x) \) and \( \arctan(x) \) is specified as \( |x| < 1 \), illustrating the need for caution at the boundaries.
- 📚 The binomial series is introduced as the Taylor series for \( (1 + x)^\alpha \), with a specific focus on its applications and convergence criteria.
- 🚫 The script concludes with a reminder that while Taylor series can be powerful tools within their domain of convergence, one must be cautious when approaching or exceeding this domain.
Q & A
What is the main challenge discussed in the lecture regarding series?
-The main challenge discussed is the danger of adding together an infinite number of terms in a series, which can lead to issues with convergence and the behavior of the series.
Why is it incorrect to assume that every function has a nice Taylor series about zero?
-It is incorrect because polynomials are too simple to capture all the complexities of functions. For example, the function log(x) is not defined at x=0, making a Taylor series expansion about zero impossible.
What is a geometric series and what does it converge to?
-A geometric series is an infinite series of the form 1 + x + x^2 + x^3 + ..., where x is a constant. It converges to 1 / (1 - x), provided that the absolute value of x is less than 1.
How does the geometric series formula apply to the sum of 1 + 1/2 + 1/4 + ...?
-The sum 1 + 1/2 + 1/4 + ... is a geometric series with x = 1/2. According to the formula, it converges to 1 / (1 - 1/2), which simplifies to 2.
What is the general formula for a geometric series?
-The general formula for a geometric series is the sum from k=0 to infinity of x^k, which equals 1 / (1 - x), where x is the common ratio of the series.
Why does the derivation of the geometric series formula only hold for values of x less than 1?
-The derivation only holds for values of x less than 1 in absolute value because beyond this range, the series does not converge, meaning the sum does not approach a finite value.
What is the issue with the series 1 - 1 + 1 - 1 + ... when x = -1?
-The issue is that the series does not converge; it oscillates between different values depending on how the terms are paired, and thus it does not have a well-defined sum.
How does the domain of convergence affect the manipulation of a Taylor series?
-Within the domain of convergence, a Taylor series can be manipulated freely, such as rearranging terms, differentiating, or integrating term by term. However, one must be careful near the borders of the domain.
What is the Taylor series for log(1 + x) and under what condition does it converge?
-The Taylor series for log(1 + x) is -x + x^2/2 - x^3/3 + ..., which is a series without factorials in the denominators. It converges when the absolute value of x is less than 1.
What is the binomial series and how does it relate to the geometric series?
-The binomial series is the Taylor series for (1 + x)^alpha, where alpha is a constant. It is related to the geometric series when alpha equals -1, as it represents 1 / (1 + x), which is a variation of the geometric series.
Why is the binomial series only valid for certain values of x?
-The binomial series is only valid when the absolute value of x is less than 1 because it is derived from the geometric series, which converges only within this range.
Outlines
📚 Introduction to Series Convergence
Professor Greist begins Lecture 5 of Calculus by addressing the challenge of series convergence. He explains that adding an infinite number of terms can be problematic, especially when functions like log(X) do not have a Taylor series around zero. The professor introduces the concept of geometric series as an example of a series that converges to a finite sum, specifically 2 for the series 1 + 1/2 + 1/2^2 + ..., and provides a general formula for geometric series. He also discusses the importance of the domain of convergence and the conditions under which series manipulations are valid.
🔍 Exploring the Domain of Convergence
The second paragraph delves deeper into the domain of convergence, emphasizing that while some series like the exponential function, sine, and cosine converge over the entire real line, others like the geometric series require more caution. The professor illustrates this with the example of the sum 1 - 1 + 1 - 1 + ..., which does not converge for x = -1, and explains that the domain of convergence is crucial for the validity of series manipulations. He also discusses the Taylor series of log(1 + X), derived by integrating the geometric series at negative X, and highlights the importance of staying within the convergence domain for accurate approximations.
📉 Series Approximations and Their Limitations
In the third paragraph, the professor examines the approximation capabilities of Taylor series, using the log(1 + X) series as an example to show how the approximation improves within the domain of convergence (-1 < X < 1) but deteriorates outside of it. He then introduces the arctan function and its Taylor series, derived from the geometric series representation of 1/(1 + X^2), and reiterates the importance of the convergence domain. The binomial series is also introduced, with examples of how it can be used to find Taylor series for functions like the square root of (1 + X), with the caveat that it only converges for |X| < 1.
🌟 Conclusion: The Importance of Domain of Convergence
The final paragraph summarizes the lesson by emphasizing the importance of the domain of convergence for the validity of Taylor series. The professor presents a collection of Taylor series that are guaranteed to converge only when |X| < 1, including the geometric series, log(1 + X), arctan, and the binomial series. He advises that as long as one stays within the domain of convergence, these series can be used for various mathematical manipulations and approximations, and hints at the next lesson's focus on expansion points for specific locations.
Mindmap
Keywords
💡Convergence
💡Geometric Series
💡Taylor Series
💡Domain of Convergence
💡Logarithmic Function
💡Algebraic Manipulation
💡Infinite Series
💡Binomial Series
💡Arc Tangent Function (arctan)
💡Series Manipulation
Highlights
Introduction to the concept of convergence in calculus and its importance in handling infinite series.
The challenge of adding an infinite number of terms and the inherent dangers involved.
The limitations of Taylor series, especially for functions like log(x) which are not defined at x=0.
The simplicity of polynomials and their inability to capture all complexities of functions.
The geometric series as an example of a convergent infinite series, summing to 2 when evaluated at 1/2.
The general formula for a geometric series and its convergence to 1/(1-X).
A proof technique for the convergence of geometric series using algebraic manipulation.
The divergence of the geometric series when X=1, demonstrating the importance of the domain of convergence.
The indeterminate form of the geometric series at X=-1 and the implications for convergence.
The binomial series as a special case of the Taylor series for (1+X)^alpha.
The importance of the domain of convergence for the validity of Taylor series.
The Taylor series for log(1+X) derived from the integral of 1/(1+X).
The manipulation of known series to find the Taylor series for functions like arctan(x).
The practical applications of Taylor series within their domain of convergence, such as term-by-term differentiation and integration.
The caution required when dealing with the borders of the domain of convergence.
The limitations of polynomial approximations outside of their domain of convergence.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: