Function as a geometric series | Series | AP Calculus BC | Khan Academy

Khan Academy
26 Dec 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains how to find a power series for the function f(x) = 6 / (1 + x^3) by recognizing its similarity to a geometric series. Instead of using the Maclaurin series, the instructor suggests a simpler approach by treating the function as a sum of a geometric series, making the expansion straightforward and highlighting a useful trick for power series expansions.

Takeaways
  • 📚 The task is to find a power series for a given function f(x) = \( \frac{6}{1 + x^3} \).
  • 🔍 The instructor suggests considering the Maclaurin series for simplicity, as it is centered at zero.
  • 🚫 Directly finding the Maclaurin series by evaluating derivatives at zero can become complex quickly.
  • 💡 A simplification is proposed by considering f(u) = \( \frac{6}{1 + u} \) where u = x^3 to make the expansion easier.
  • 🔑 The instructor identifies that the function resembles a geometric series and suggests using this property for expansion.
  • 📈 The sum of a geometric series is given by \( a / (1 - r) \), where a is the first term and r is the common ratio.
  • 📝 The function f(x) can be rewritten to fit the geometric series formula by setting a = 6 and r = -x^3.
  • 🌟 Recognizing the function as a geometric series allows for a straightforward power series expansion without complex derivatives.
  • 📉 The power series expansion is written out as a series of terms involving x raised to increasing odd powers, multiplied by 6.
  • 🔁 The series continues indefinitely, with each term being \( 6x^{3n} \) where n is a non-negative integer.
  • 🛠 This approach is highlighted as a useful trick for simplifying the process of finding power series expansions for certain types of functions.
Q & A

  • What is the function f(x) given in the script?

    -The function f(x) given in the script is f(x) = 6 / (1 + x^3).

  • Why is the Maclaurin series a common choice for a power series expansion?

    -The Maclaurin series is a common choice because it is centered at zero and tends to be the simplest to find, especially when evaluating functions at their derivatives at zero.

  • What is the main challenge when finding the Maclaurin series for the given function?

    -The main challenge is that after evaluating the first few derivatives, the process becomes very complex and 'hairy', making it difficult to continue.

  • What is the alternative approach suggested in the script to simplify the process?

    -The alternative approach is to express f(x) as f(u) = 6 / (1 + u) where u = x^3, find the Maclaurin expansion in terms of u, and then substitute x^3 back in.

  • What does the instructor suggest as the simplest way to approach the problem?

    -The simplest way suggested is to recognize that the given function looks similar to the sum of a geometric series and to use that to find the power series expansion.

  • What is the sum of a geometric series formula?

    -The sum of a geometric series is given by a / (1 - r), where 'a' is the first term and 'r' is the common ratio.

  • How does the instructor relate the given function to the sum of a geometric series?

    -The instructor relates the function by setting 'a' to 6 and considering 'r' as -x^3, rewriting the denominator as 1 - (-x^3) and then expanding it as a geometric series.

  • What is the first term (a) of the geometric series representation of the function?

    -The first term (a) of the geometric series representation is 6.

  • What is the common ratio (r) of the geometric series representation of the function?

    -The common ratio (r) is -x^3.

  • What is the significance of recognizing the function as a geometric series?

    -Recognizing the function as a geometric series allows for a straightforward expansion without the need for complex derivative calculations, making it a very useful trick for finding the power series expansion.

  • How does the instructor expand the function as a geometric series?

    -The instructor expands the function by multiplying the first term 6 by the common ratio -x^3 repeatedly, resulting in terms like -6x^3, 6x^6, -6x^9, and so on, continuing indefinitely.

Outlines
00:00
📚 Introduction to Power Series Expansion

The instructor begins by discussing the task of finding a power series for the function f(x) = 6 / (1 + x^3). They suggest starting with the Maclaurin series, which is typically the simplest to find due to its center at zero. The process involves evaluating the function and its derivatives at zero and then using the Maclaurin series formula to expand it. However, the instructor quickly points out that this method can become complex when dealing with higher derivatives. Instead, they propose a simplification by finding the Maclaurin series for a related function f(u) = 6 / (1 + u), where u = x^3, and then substituting back for x^3. This approach is deemed simpler, but the instructor ultimately highlights that the function resembles a geometric series, which can be directly expanded without the need for derivatives.

Mindmap
Keywords
💡Power Series
A power series is an infinite series of the form \( \sum_{n=0}^{\infty} a_n (x - c)^n \), where \( a_n \) are the coefficients and \( c \) is the center of the series. In the video, the instructor is tasked with finding a power series representation for a given function, which is a fundamental concept in calculus and mathematical analysis. The power series is central to the theme of the video as it is the method used to expand the function.
💡Maclaurin Series
The Maclaurin series is a specific type of power series, named after Colin Maclaurin, which is centered at \( x = 0 \). It is used to represent functions as a sum of a series of terms involving powers of \( x \). The instructor considers using the Maclaurin series for simplicity but finds it challenging due to the complexity of the derivatives involved. The concept is integral to the video's narrative as it represents one approach to finding the power series.
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. The instructor mentions evaluating the first and second derivatives of the function at zero, which is a standard step in finding the Maclaurin series. Derivatives are essential in understanding how the function behaves and in calculating the coefficients of the power series.
💡Geometric Series
A geometric series is a series of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. The instructor identifies the given function as resembling a geometric series, which simplifies the process of finding the power series. The geometric series is a key concept in the video as it provides an alternative and simpler method to expand the function.
💡Common Ratio
In the context of a geometric series, the common ratio is the factor by which we multiply each term to get the next. In the video, the common ratio is identified as \( -x^3 \), which is crucial for the expansion of the power series as it dictates the pattern of the series.
💡Rational Expression
A rational expression is a mathematical expression that can be written as the quotient of two polynomials. The function given in the video is a rational expression, and the instructor notes its similarity to the sum of a geometric series. Recognizing the function as a rational expression is important for the video's theme as it leads to the realization that the function can be expanded as a geometric series.
💡Series Expansion
Series expansion refers to the process of expressing a function as an infinite series. In the video, the instructor is looking to express the given function as a power series, specifically a geometric series. The series expansion is the main goal of the video, and the method chosen for the expansion is central to the instructional content.
💡First Term
In a geometric series, the first term is the initial value of the series before any multiplication by the common ratio. In the video, the first term is identified as 6, which is the starting point for the series expansion of the function.
💡Sum of a Series
The sum of a series is the result of adding all the terms of the series together. The instructor uses the formula for the sum of a geometric series to find the power series expansion of the function. Understanding the sum of a series is essential for the video's message as it provides the formula used to express the function as a series.
💡Infinite Series
An infinite series is a series that has an infinite number of terms. The power series and geometric series discussed in the video are both infinite, which is a key characteristic as it allows for the representation of functions over a continuous range of values.
💡Simplification
Simplification in mathematics refers to making a complex problem or expression easier to understand or solve. The instructor simplifies the problem by recognizing the function as a geometric series, which avoids the complexity of higher derivatives. Simplification is a key concept in the video as it demonstrates a strategic approach to solving mathematical problems.
Highlights

Introduction of the task to find a power series for a given function f(x).

Suggestion to use the Maclaurin series due to its simplicity when centered at zero.

The challenge of evaluating higher derivatives in the Maclaurin series approach.

Proposal to simplify by finding the Maclaurin series for a transformed function f(u).

Recognition of the function's resemblance to a geometric series.

Explanation of the sum of a geometric series formula.

Identification of 'a' as 6 and 'r' as -x^3 in the context of the given function.

Transformation of the denominator to one minus the common ratio.

Expansion of the function into a geometric series.

Writing out the first few terms of the geometric series for f(x).

Illustration of the process to continue the series indefinitely.

The key insight that the function can be considered a sum of a geometric series.

Highlighting the usefulness of recognizing the function's form to simplify the power series expansion.

Emphasis on avoiding complex derivative calculations by using the geometric series approach.

Final note on the simplicity and effectiveness of the geometric series method for this problem.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 10.14 Part 2

Power series intro | Series | AP Calculus BC | Khan Academy

Worked example: power series from cos(x) | Series | AP Calculus BC | Khan Academy

Geometric series interval of convergence | Series | AP Calculus BC | Khan Academy

Integrating power series | Series | AP Calculus BC | Khan Academy

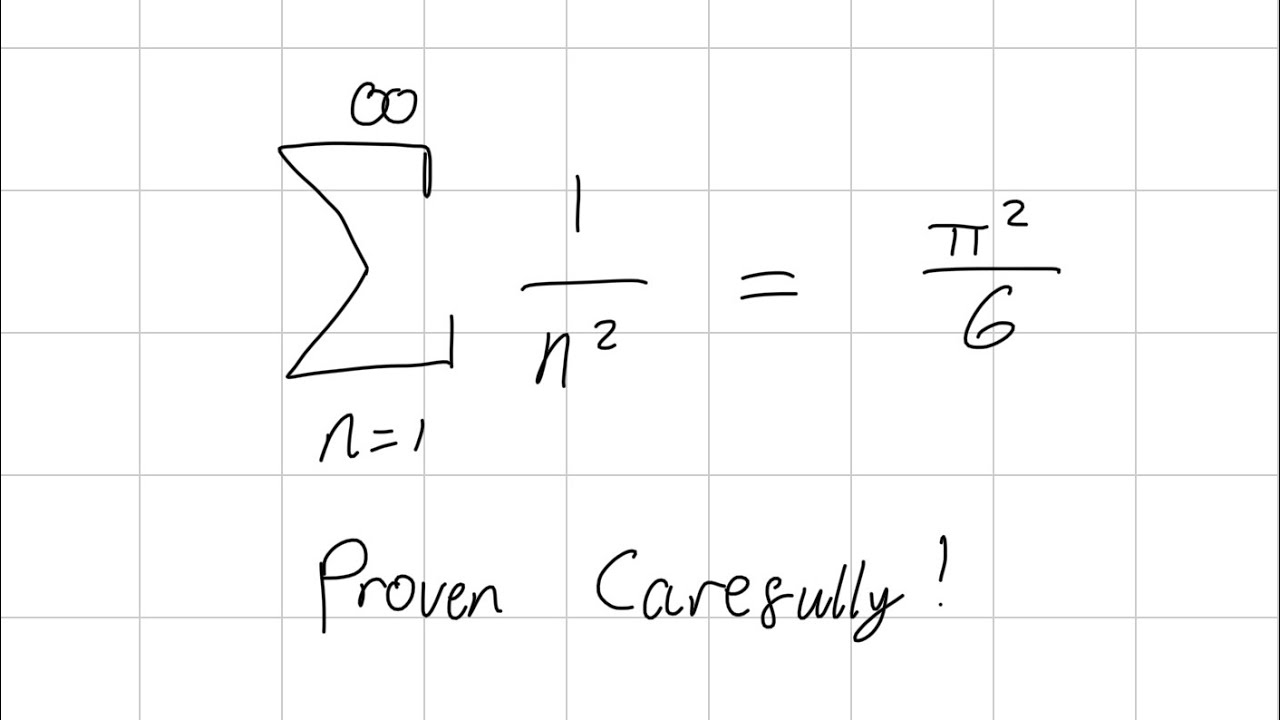
Proof Of The Basel Problem

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Power SeriesGeometric SeriesMaclaurin SeriesSeries ExpansionMathematicsCalculusFunction AnalysisEducational ContentTrigonometric FunctionsAlgebraic Simplification