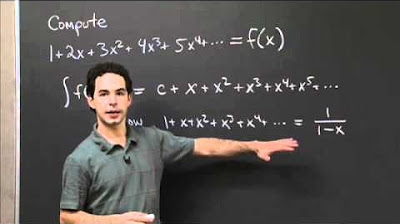AP Calculus BC Lesson 10.14 Part 2

Elizabeth Fein

28 Mar 202321:51

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial delves into the concept of geometric series and its application in power series, particularly within the context of Taylor and Maclaurin series. It begins with a review of geometric series, highlighting the convergence condition and the formula for the sum of a convergent series. The video then demonstrates how to use geometric series to simplify the process of finding the Maclaurin series for functions like 1/(1-x) and 1/(1-x^3), emphasizing the importance of the interval of convergence. The tutorial also covers the use of the quotient rule for derivatives and provides examples of calculating the Taylor series for specific functions, including finding the coefficient of a particular term and evaluating the function at a given point. The content is presented in a structured manner, with clear explanations and step-by-step calculations, making it accessible for viewers looking to enhance their understanding of these mathematical concepts.

Takeaways

📘 The video discusses a geometric series shortcut useful with power series.
🔍 A brief review of geometric series from lesson 10.2 is provided, emphasizing the convergence condition (absolute value of R < 1) and the sum formula (a / (1 - R)).
📈 Functions like 1 / (1 - X) can be represented as geometric series within their interval of convergence.
🌟 The Maclaurin series for a function f(x) involves finding derivatives at zero and can be simplified using geometric series concepts.
📊 The process of finding the Maclaurin series for a function is illustrated through the example of f(x) = 1 / (1 - x).
🔑 The shortcut for finding the Maclaurin series involves identifying the values of A (first term) and R (common ratio) from the function's expression.
📝 The general term of a power series is given by a * R^n, where n starts from 0 and increases to infinity.
🏹 The interval of convergence for a geometric series is determined by ensuring the absolute value of R is less than 1.
🧩 The video provides examples of finding the Taylor series for different functions centered at x=0, including the first few non-zero terms and the general term.
🔍 The process of finding the coefficient of a specific term in the Taylor series is demonstrated, using the function f(x) = 1 / (4 + x).
📌 The video concludes with examples of power series expansions for given rational functions and determining their intervals of convergence.

Q & A

What is the definition of a geometric series?
-A geometric series is a series of the form ∑ from n=0 to Infinity of a times R to the power of n, where 'a' is the starting term and 'R' is the common ratio.
Under what condition does a geometric series converge?
-A geometric series converges if the absolute value of the common ratio 'R' is less than one.
What is the formula to find the sum of a convergent geometric series?
-The sum of a convergent geometric series is given by the formula S = a / (1 - R), where 'a' is the first term of the series.
How can the geometric series shortcut be used with power series?
-The geometric series shortcut can be used with power series by representing functions in the form of a geometric series within their interval of convergence, simplifying the process of finding the power series.
What is the Maclaurin series for the function f(x) = 1 / (1 - x)?
-The Maclaurin series for f(x) = 1 / (1 - x) is given by ∑ from n=0 to Infinity of x^n, which simplifies to 1 + x + x^2 + x^3 + ..., within the interval of convergence (|x| < 1).
How can you find the Taylor series for a function centered at x = 0?
-To find the Taylor series for a function centered at x = 0, you would take the derivatives of the function at x = 0 and use them in the Taylor series formula, which is a sum of terms calculated as f^(n)(0) * x^n / n!.
What is the interval of convergence for the geometric series 1 / (1 - x^3)?
-The interval of convergence for the geometric series 1 / (1 - x^3) is (-1, 1), meaning x must be between -1 and 1 for the series to converge.
How do you find the coefficient of a specific term in a Taylor series?
-To find the coefficient of a specific term in a Taylor series, you identify the term that includes the desired power of x and then evaluate the series at that power, considering the general term formula of the series.
What is the Maclaurin series for the function f(x) = 1 / (4 + x)?
-The Maclaurin series for f(x) = 1 / (4 + x) is given by ∑ from n=0 to Infinity of (-x)^n / 4^(n+1), which simplifies to 1 - x/4 + x^2/16 - x^3/64 + ..., within the interval of convergence (|x| < 4).
What is the value of f(2) for the Maclaurin series ∑ from n=0 to Infinity of (-2/3)^n?
-The value of f(2) for the Maclaurin series ∑ from n=0 to Infinity of (-2/3)^n is 3/5 or 0.6, as it is the sum of the series when x = 2.
Which power series expansion corresponds to the function (x^3) / (1 + x^3)?
-The power series expansion for the function (x^3) / (1 + x^3) corresponds to the series ∑ from n=0 to Infinity of (-1)^n * x^(3n), which is the same as the series in answer choice A.

Outlines

00:00

📚 Introduction to Geometric Series Shortcut

This paragraph introduces a shortcut for geometric series in the context of power series. It begins with a review of geometric series from lesson 10.2, emphasizing the formula for the sum of a geometric series as 'a / (1 - r)' when 'r' is less than 1. The paragraph then transitions into discussing the application of this formula with power series, specifically for functions like '1 / (1 - x)' and related rational functions. The process of finding the Maclaurin series through derivatives is outlined, highlighting the cumbersome nature of this method and setting the stage for the introduction of the geometric series shortcut.

05:01

🔍 Applying the Geometric Series Shortcut

The paragraph delves into the application of the geometric series shortcut for functions that can be represented as a geometric series. It provides a step-by-step explanation of how to rewrite a function as a series and how to identify the 'a' and 'r' values. The paragraph demonstrates the process with the function '1 / (1 - x)', showing how to write its Maclaurin series using the geometric series formula. It emphasizes the importance of the interval of convergence and provides the series expansion for the function, including the first few terms and the general term.

10:01

📈 Calculating Specific Terms and Intervals of Convergence

This paragraph focuses on calculating specific terms of a Taylor series and determining the interval of convergence. It provides examples of how to find the first few non-zero terms and the general term for the series '1 / (1 - x^3)' and '4 / (2 + x)'. The paragraph also explains how to find the interval of convergence for these series, using the absolute value of 'r' being less than one as the guiding principle. The process is illustrated with clear calculations and explanations, leading to the identification of the interval of convergence for each series.

15:02

🔢 Coefficient Extraction in Taylor Series

The paragraph discusses the method for extracting a specific coefficient in a Taylor series. It uses the function 'f(x) = 1 / (4 + x)' to illustrate how to find the coefficient of 'x^3' in its Taylor series centered at 'x = 0'. The process involves transforming the function into a recognizable form and then identifying the 'a' and 'r' values for the geometric series representation. The paragraph provides a detailed calculation to find the coefficient, which is '-1/256', and confirmss that the correct choice is option B.

20:05

📊 Evaluating a Function at a Specific Point

This paragraph demonstrates how to evaluate a function at a specific point using its Maclaurin series. It focuses on the function 'f(x) = Sum(n from 0 to Infinity) of (-x^3)/3^n' and calculates the value of 'f(2)'. The process involves substituting 'x' with '2' in the series and simplifying the resulting expression. The paragraph shows the step-by-step simplification, leading to the conclusion that 'f(2)' equals '3/5', which corresponds to choice C.

🌟 Power Series Expansion for Rational Functions

The final paragraph addresses the task of finding a power series expansion for a given rational function, 'x^3 / (1 + x^3)'. It explains how to rearrange the function into the 'a / (1 - r)' form, where 'a' is 'x^3' and 'r' is '-x^3'. The paragraph then outlines the process of writing out the series, including the first few terms and the general term. It confirms that the correct expansion matches choice A, providing a clear and comprehensive explanation of the power series representation for the given rational function.

Mindmap

Keywords

💡Geometric Series

A geometric series is a sequence of terms where each term is found by multiplying the previous term by a fixed, non-zero number called the common ratio. In the context of the video, it is a fundamental concept used to discuss shortcuts in conjunction with power series. The series is defined as the sum from n equals 0 to infinity of a term 'a' times 'r' to the power of 'n'. The series converges if the absolute value of 'r' is less than one.

💡Power Series

A power series is an infinite series that represents a function as the sum of terms that are products of a variable and non-negative integer powers of that variable. In the video, power series are used to approximate functions and find their derivatives and integrals. The general form of a power series is 'sum from n equals 0 to infinity of a_n * (x - c)^n', where 'a_n' are the coefficients and 'c' is the center of the series.

💡Maclaurin Series

A Maclaurin series is a special case of a Taylor series, which is a power series representation of a function expanded around zero. It is used to approximate functions and find their derivatives at zero. The Maclaurin series for a function 'f(x)' is given by 'f(x) = f(0) + f'(0)x + f''(0)x^2/2! + ...' and requires calculating the derivatives of the function at x=0.

💡Convergence

In mathematics, convergence refers to the property of a sequence or series to approach a certain value as the number of terms increases. A geometric series converges if the absolute value of its common ratio 'r' is less than 1. In the context of the video, convergence is a critical condition for the sum of a geometric series to be defined and for the application of power series to be valid.

💡Common Ratio (R)

The common ratio 'R' in a geometric series is the factor by which each term is multiplied to obtain the next term in the sequence. It is a key component in determining the convergence of a geometric series and is used in the formula for the sum of a convergent series. In power series, 'R' often represents the variable (x) in the series expansion.

💡Taylor Series

A Taylor series is a representation of a function as an infinite sum of terms calculated from its derivatives at a single point, known as the center of the series. It is used to approximate functions and find their derivatives and integrals at any point within the interval of convergence. The general form of a Taylor series is 'f(x) = sum from n equals 0 to infinity of [f^n(c) / n!] * (x - c)^n', where 'c' is the center and 'f^n(c)' denotes the nth derivative of 'f' evaluated at 'c'.

💡Derivatives

Derivatives are a fundamental concept in calculus that represent the rate of change of a function with respect to its variable. In the context of the video, derivatives are used to construct the Maclaurin and Taylor series for functions, which involves finding the first, second, and higher order derivatives at the center of the series.

💡Interval of Convergence

The interval of convergence for a power series is the range of values for the variable over which the series converges to a function. It is determined by the common ratio 'R' in the geometric series and is critical for the validity of the power series representation of a function. The interval is often expressed as an inequality involving the absolute value of 'R'.

💡Quotient Rule

The quotient rule is a fundamental algebraic identity used to find the derivative of a quotient of two functions. It states that the derivative of a function 'f(x) / g(x)' is equal to '(f'(x)g(x) - f(x)g'(x)) / g(x)^2'. In the video, the quotient rule is used to find the derivatives of the function 'f(x) = 1/(1-x)' when constructing its Maclaurin series.

💡Simplifying

Simplifying in mathematics refers to the process of reducing a complex expression or equation to a simpler form. In the context of the video, simplifying is used to make the expressions for power series and their coefficients more manageable and easier to understand. This often involves combining like terms, reducing fractions, and applying algebraic rules.

💡Coefficients

Coefficients are the numerical factors in a power series that multiply the variable raised to a certain power. They determine the shape and behavior of the series and are crucial for accurately representing the function by the series. In the video, coefficients are calculated as part of constructing the power series for given functions.

Highlights

Discussion of a geometric series shortcut for power series.

Brief review of geometric series from lesson 10.2.

Convergence of geometric series when the absolute value of R is less than one.

Sum of a geometric series is a over 1 minus R.

Working with functions like f(x) = 1/(1-x) using geometric series.

Representing rational functions as geometric series within the interval of convergence.

Maclaurin series calculation using derivatives at zero.

Shortcut for Maclaurin series using geometric series simplifies calculations.

Maclaurin series for f(x) = 1/(1-x) is 1 + x + x^2 + ...

Interval of convergence for geometric series is crucial for the validity of the series.

Maclaurin series for 1/(1-x^3) including first three non-zero terms and the general term.

Interval of convergence for 1/(1-x^3) is between -1 and 1.

Power series for 4/(2+x) including first four non-zero terms and the general term.

Interval of convergence for 4/(2+x) is between -2 and 2.

Taylor series for 1/(3+x^2) including first four non-zero terms and the general term.

Interval of convergence for 1/(3+x^2) is between -sqrt(3) and sqrt(3).

Coefficient of x^3 in the Taylor series for f(x) = 1/(4+x) is -1/256.

Value of f(2) for the Maclaurin series f(x) = sum from n=0 to Infinity of (-2/3)^n.

Transcripts

Browse More Related Video

Finding Taylor Series

Geometric Series Summing to Functions

Integration of Taylor's Series | MIT 18.01SC Single Variable Calculus, Fall 2010

Calculus Chapter 1 Lecture 5 Convergence

Function as a geometric series | Series | AP Calculus BC | Khan Academy

AP Calculus BC Exam Review - Geometric Series

Related Tags

Mathematics Geometric Series Power Series Maclaurin Series Taylor Series Rational Functions Series Convergence Math Tutorial Educational Content Mathematics Education