Volumes with Disks

RH Mathematics

10 May 202112:49

EducationalLearning

32 Likes 10 Comments

TLDRThis script outlines a three-part video series on volume calculations in AP Calculus, focusing on the disk method. The first video introduces the concept of rotating a region around an axis to form a solid, exemplified by the graph of y = sqrt(x). The instructor explains the technique, emphasizing that the region must always touch the axis of rotation. The script also briefly mentions the washer method and volume with known cross sections, which will be covered in subsequent videos. The examples provided illustrate how to calculate the volume of solids formed by revolving around the x and y axes, using integrals of pi times the radius squared, with the radius expressed in terms of the variable of integration.

Takeaways

📚 The script introduces three main techniques for calculating volume in AP Calculus: the disk technique, the washer technique, and volume of solids with known cross sections.
📐 The disk technique involves rotating a region around an axis to form a solid, which is then calculated by summing up the volumes of infinitesimally thin disks.
🚫 The shell technique is not included in the AP Calculus course anymore and will not be covered in the initial videos but might be discussed later.
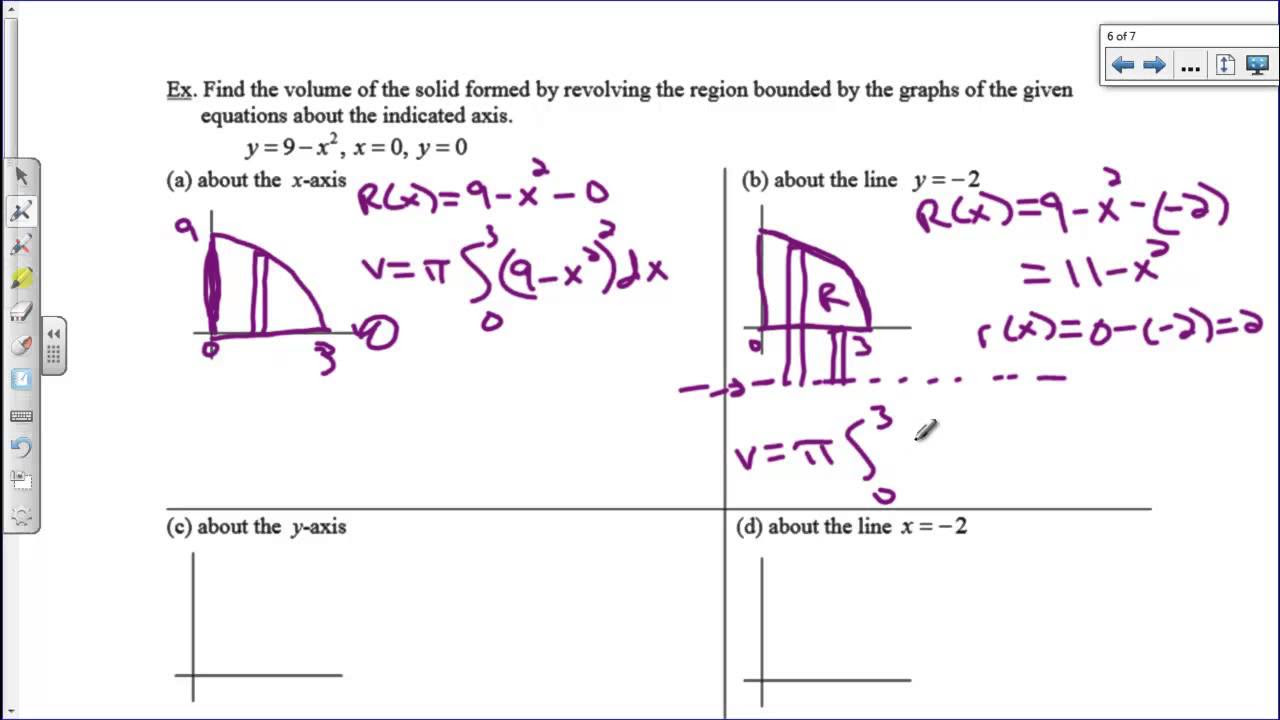
🍩 The first example uses the graph of y = √x rotated around the x-axis to form a solid resembling a 'gumdrop' shape, illustrating the disk technique.
📉 The volume of a solid formed by the disk technique is calculated by integrating π * r^2 with respect to the appropriate variable (x or y), depending on the axis of rotation.
🔢 The radius 'r' for the disk method is determined by the distance from the axis of rotation to the curve, ensuring the region is always touching the axis.
📈 The volume calculation involves setting up an integral where the radius is expressed in terms of the variable of integration, simplifying the expression before integrating.
⚖️ The example with y = e^x and y = 10 rotated around the y-axis demonstrates how to find the radius 'r' as the difference between the y-values at the axis of rotation and the curve.
📊 The script emphasizes the importance of setting up the integral correctly, even if the anti-derivative is not immediately known, as it represents the volume of the solid.
📝 The video mentions that students should practice setting up integrals for volume calculations, especially when the integrand is complex or requires the use of logarithmic properties.
📘 The script suggests further practice with additional videos on the washer technique and volume with known cross sections, as well as completing quiz 8.2 for more problems.

Q & A

What are the three volume techniques discussed in the AP Calculus course?
-The three volume techniques discussed in the AP Calculus course are the Disk Method, the Washer Method, and the method involving solids with known cross sections.
Why is the Shell Method not included in the AP Calculus course anymore?
-The Shell Method is not included in the AP Calculus course anymore because it has been removed from the curriculum. However, it might still be expected knowledge in some higher-level math courses or university classes.
What does the Disk Method involve when calculating volumes?
-The Disk Method involves rotating a region around an axis to form a solid and then calculating the volume by summing up the volumes of infinitesimally small disks that make up the solid.
How is the volume of a solid formed by rotating the graph of y = √x around the x-axis calculated?
-The volume is calculated using the integral of π times the radius squared dx, where the radius is the distance from the x-axis to the curve (√x), integrated from x = 0 to x = 16.
What is the significance of the radius in the Disk Method?
-The radius in the Disk Method is the distance from the axis of rotation to the curve that defines the region being rotated. It is crucial for determining the area of the disk faces that make up the volume of the solid.
What happens if the region being rotated does not touch the axis of rotation at all times?
-If the region does not touch the axis of rotation at all times, the Disk Method is not applicable. Instead, the Washer Method should be used to calculate the volume.
What is the formula used to calculate the volume of a solid when using the Disk Method?
-The formula used to calculate the volume of a solid using the Disk Method is the integral of π times the radius squared with respect to the appropriate variable (dx for horizontal rotation, dy for vertical rotation).
How does the axis of rotation affect the orientation of the disks in the Disk Method?
-The axis of rotation determines whether the disks are oriented horizontally or vertically. For horizontal rotation around the x-axis, the disks slide up and down, while for vertical rotation around the y-axis, they extend outward.
What is the primary concept that connects the calculation of volume in the Disk Method to other topics in calculus?
-The primary concept that connects the calculation of volume in the Disk Method to other topics in calculus is the Riemann Sum, which is used to approximate the area under a curve and is the foundation for integral calculus.
What is the role of the radius in the calculation of volume when rotating the region enclosed by y = e^x and y = 10 around the y-axis?
-The radius in this calculation is the horizontal distance from the y-axis to the curve, which is determined by the difference between the y-values of the two functions at a given x-value (log(y) in this case).

Outlines

00:00

📚 Introduction to Volume Techniques in AP Calculus

This paragraph introduces the video series on volume techniques in AP Calculus, starting with the disk method for rotating regions around an axis. It mentions upcoming videos on the washer technique, which deals with volumes having gaps, and volumes of solids with known cross-sections. It also notes the exclusion of the shell technique from the AP Calculus curriculum and its relevance in higher-level courses.

05:01

🌀 Volume with the Disk Method: First Example

This paragraph explains the first example of using the disk method to find the volume of a solid. It describes rotating the graph of y = √x around the x-axis, forming a solid resembling a gumdrop. The explanation includes visualizing the solid and the importance of the Riemann sum concept in calculating the volume by adding up infinitesimally small disks.

10:04

🔄 Integrating to Find Volume Using Disks

This section delves into the mathematical process of finding the volume using the disk method. It describes calculating the volume by integrating the area of each disk (πr²) along the x-axis, from x = 0 to x = 16. The integral setup and calculation are detailed, including factoring out constants and evaluating the definite integral to obtain the final volume.

📏 Example with e^x: Disk Method for a Vertical Axis

This paragraph presents another example using the disk method, rotating the region bounded by y = e^x, y = 10, and the y-axis around the y-axis. It explains the integral setup for this scenario, converting the function into terms of y and setting the limits of integration from y = 1 to y = 10. The calculation involves finding the radius as log(y) and setting up the integral to represent the volume.

🔄 Rotating Around a Line: Advanced Disk Method Example

This example involves rotating the region around the line x = 16 to find the volume. It describes the disk method setup, where the radius is determined as the distance from the axis of rotation (x = 16) to the curve y = √x. The paragraph covers the integral setup with respect to y, from y = 0 to y = 4 (√16), and mentions the process of squaring the radius and integrating.

🌐 Volume of Solids with Non-Standard Axes

In this section, the volume of the region bounded by y = e^x, y = 10, and the y-axis is calculated by rotating around y = 10. It explains how the radius is determined by the difference between the top (y = 10) and the curve (y = e^x). The integral is set up with respect to x, from x = 0 to x = log(10), and involves squaring the radius and integrating to find the volume.

📘 Conclusion and Additional Resources

The final paragraph concludes the discussion on the disk method, referring viewers to the next videos on the washer method and cross-sections for more examples. It suggests practice problems from a specific quiz and reminds viewers of the importance of understanding related concepts such as arc length.

Mindmap

Keywords

💡Volume

Volume in the context of this video refers to the amount of space occupied by a solid object, which is a fundamental concept in calculus when dealing with three-dimensional shapes. The video focuses on calculating volumes of solids formed by rotating regions around an axis. For example, the script discusses calculating the volume of a solid formed by rotating the graph of y = √x around the x-axis.

💡Disk Technique

The disk technique is a method used in calculus to find the volume of a solid generated by revolving a region around an axis. The video script describes this technique as revolving a region around the x-axis, forming a solid that can be visualized as a series of infinitesimally thin disks stacked on top of each other. The volume is then calculated by integrating the area of these disks over the interval of rotation.

💡AP Calculus

AP Calculus is a high school course that covers advanced topics in calculus, preparing students for college-level mathematics. The video script mentions that the techniques discussed, such as the disk technique, are essential for students taking AP Calculus exams. It also notes that the shell method, while not included in the AP Calculus course, is a related technique that might be expected in higher-level calculus courses.

💡Riemann Sum

The Riemann Sum is a method used in calculus to approximate the area under a curve by summing the areas of rectangles. In the video, the concept is extended to volume, where the volume of a solid is approximated by summing the volumes of infinitesimally thin disks (in the case of the disk technique). The script connects this idea to the fundamental principles of calculus, emphasizing its relevance in calculating volumes.

💡Integral

An integral in calculus is a mathematical operation that represents the process of summing up an infinite number of infinitesimally small quantities. In the video, the integral is used to calculate the volume of solids by summing up the volumes of the infinitesimally thin disks formed by the disk technique. The script mentions integrating pi * r^2 dx or dy, depending on the axis of rotation.

💡Graph of y = √x

The graph of y = √x is a mathematical function that describes a curve where the y-value is the square root of the x-value. In the video, this graph is used as an example to demonstrate how a solid is formed by rotating the region around the x-axis, resulting in a shape that resembles a 'gumdrop'.

💡Axis of Rotation

The axis of rotation is the line or plane around which a region is rotated to form a solid. In the video, different axes of rotation are discussed, such as the x-axis and the y-axis, and the line y = 10. The script emphasizes that the region being rotated must touch the axis at all times for the disk technique to be applicable.

💡Logarithm

A logarithm is a mathematical function that is the inverse of exponentiation. In the video script, the logarithm is used to express x in terms of y for the curve y = e^x, which is necessary for setting up the integral to find the volume of a solid formed by rotating this curve around the y-axis.

💡Washer Technique

The washer technique is another method used in calculus to find the volume of a solid formed by revolving a region around an axis, but unlike the disk technique, there is a gap in the middle of the solid. The video script mentions this technique but focuses primarily on the disk technique, indicating that the washer technique will be covered in a separate video.

💡Solids with Known Cross Sections

Solids with known cross sections are a type of three-dimensional shape where the cross section at any point along the axis of rotation is a known geometric shape. The video script mentions this as one of the volume techniques that will be covered in a future video, indicating that it is another method for calculating volumes in AP Calculus.

Highlights

Introduction to the first of three videos on volume in AP Calculus.

Explanation of the disk technique for finding volume by rotating a region around an axis.

Announcement of upcoming videos on the washer technique and volume of solids with known cross sections.

Clarification that the shell technique is no longer included in the AP Calculus course.

Illustration of the disk technique with an example of rotating y = sqrt(x) around the x-axis.

Description of the solid formed by the rotation as resembling a 'gumdrop'.

Discussion on the importance of the region touching the axis of rotation at all times for the disk technique.

Introduction of the Riemann sum concept in the context of finding volume.

Calculation of volume by adding up an infinite number of disks.

Conversion of the volume calculation into an integral of pi times r squared dx.

Determination of the radius r in terms of x for the integral.

Integration from x=0 to x=16 to find the volume of the solid.

Example of rotating a region enclosed by y=e^x, y=10, and the y-axis around the y-axis.

Explanation of setting up the integral for volume using the disk technique with respect to y.

Challenge of finding the antiderivative for log(y) squared without a calculator.

Demonstration of rotating the region around the line x=16 and setting up the corresponding integral.

Final example of rotating the region around the line y=10 and the setup for the integral to find volume.

Recommendation to watch additional videos on the washer technique and cross-section methods.

Advice to complete quiz 8.2 for further practice on volume calculations.

Transcripts

Browse More Related Video

Volume The Disc Method

AP Calculus AB: Lesson 7.4: Disk and Washer Method

Calculus 1: Shell Method Examples

Volume of Solids with Known Cross Sections

Shell Method - Volume of Revolution

Calculating volume by known cross sections