AP Physics B Kinematics Presentation #68

The New Jersey Center for Teaching and Learning
26 Jun 201207:19
EducationalLearning
32 Likes 10 Comments

TLDRThe script demonstrates the graphical method to find the resultant magnitude of three vector displacements. It involves breaking down each vector into its x and y components using trigonometric functions, based on their respective angles and magnitudes. After calculating the individual components, they are summed up to find the net x and y components. Finally, the magnitude of the resultant vector is determined using the Pythagorean theorem, yielding an approximate value of 60 meters.

Takeaways
  • πŸ“ The problem involves graphically determining the magnitude of the resultant vector of three given vector displacements.
  • πŸ“ The first vector is 150 meters at 30 degrees north of East.
  • πŸ“ The second vector is 220 meters at 37 degrees north of East.
  • πŸ“ The third vector is 25 meters at 45 degrees north of East.
  • πŸ” The approach is to break down each vector into its x and y components using trigonometric functions.
  • πŸ“ˆ The x-component of a vector is found using the cosine of the angle, and the y-component is found using the sine.
  • 🧩 The x and y components of each vector are then summed up to find the total x and y components of the resultant vector.
  • πŸ“Š The magnitude of the resultant vector is calculated using the Pythagorean theorem, considering the summed x and y components.
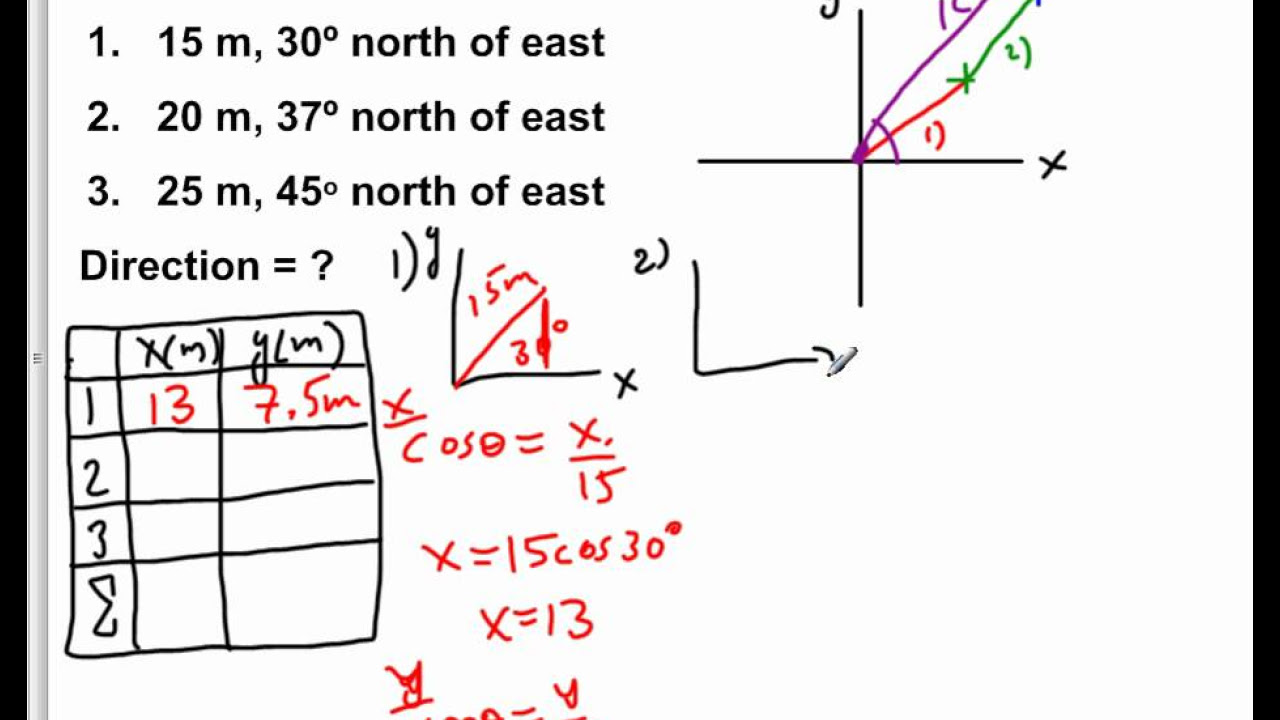
  • πŸ”’ The magnitude of the first vector's x-component is approximately 13 meters, and its y-component is 7.5 meters.
  • πŸ”’ For the second vector, the x-component is approximately 16 meters, and the y-component is 12 meters.
  • πŸ”’ The third vector's x-component is approximately 18 meters, with the y-component also being 18 meters.
  • πŸ“ The net x-component of the resultant vector is 47 meters, and the y-component is 38 meters, rounded to significant figures.
  • πŸ“ The final magnitude of the resultant vector is approximately 60 meters, calculated using the square root of the sum of the squares of the x and y components.
Q & A

  • What is the task described in the script?

    -The task is to graphically determine the magnitude of the resultant vector of three given vector displacements.

  • What are the three vector displacements mentioned in the script?

    -The three vector displacements are 150 meters at 30 degrees north of East, 220 meters at 37 degrees north of East, and 25 meters at 45 degrees north of East.

  • How does the script suggest to find the resultant vector?

    -The script suggests adding up the components of the three vectors by calculating the X and Y components for each vector and then summing them up to find the resultant vector.

  • What mathematical approach is used to find the X and Y components of each vector?

    -The script uses trigonometric functions: cosine for the X component and sine for the Y component, with the formulae being X = V * cos(ΞΈ) and Y = V * sin(ΞΈ), where V is the magnitude and ΞΈ is the angle.

  • What is the X and Y component for the first vector?

    -For the first vector, the X component is approximately 13 meters and the Y component is 7.5 meters, calculated using the cosine and sine of 30 degrees respectively.

  • What is the X and Y component for the second vector?

    -For the second vector, the X component is approximately 16 meters and the Y component is 12 meters, calculated using the cosine and sine of 37 degrees respectively.

  • What is the X and Y component for the third vector?

    -For the third vector, both the X and Y components are approximately 18 meters each, calculated using the cosine and sine of 45 degrees respectively.

  • How are the net X and Y components calculated after finding the individual components?

    -The net X component is the sum of the X components of all three vectors, which is 47 meters. The net Y component is the sum of the Y components, which is 38 meters.

  • What is the magnitude of the resultant vector calculated to be?

    -The magnitude of the resultant vector is approximately 60 meters, found by taking the square root of the sum of the squares of the net X and Y components.

  • What is the significance of using significant figures in the script?

    -Using significant figures ensures that the calculations are reported with an appropriate level of precision, avoiding overestimation of accuracy.

  • How does the script ensure the accuracy of the graphical method?

    -The script ensures accuracy by using trigonometric calculations to find the exact X and Y components and then summing these components to find the resultant vector's magnitude.

Outlines
00:00
πŸ“ Vector Addition and Resultant Magnitude Calculation

This paragraph explains the process of graphically determining the magnitude of the resultant vector from three given vector displacements. The vectors are described with their magnitudes and angles relative to East. The first vector is 150 meters at 30 degrees north of East, the second is 220 meters at 37 degrees north of East, and the third is 25 meters at 45 degrees north of East. The explanation involves breaking down each vector into its X and Y components using trigonometric functions such as cosine and sine, and then summing these components to find the resultant vector's components. The magnitude of the resultant vector is then calculated using the Pythagorean theorem.

05:02
πŸ”’ Detailed Calculation of Vector Components and Resultant

The second paragraph delves into the detailed calculations for the X and Y components of each vector. It starts by calculating the components for the first vector using the cosine and sine of 30 degrees, resulting in an X component of approximately 13 meters and a Y component of 7.5 meters. The process is repeated for the second and third vectors, yielding X and Y components of roughly 16 meters and 12 meters, and 18 meters each, respectively. After obtaining the individual components, they are summed to get the net X and Y components. The magnitude of the resultant vector is then found by applying the Pythagorean theorem to these summed components, resulting in a magnitude of approximately 60 meters.

Mindmap
Keywords
πŸ’‘Graphically determine
Graphically determine refers to the process of visually solving a problem by drawing and analyzing diagrams. In the context of the video, it is used to find the magnitude of the resultant vector by adding individual vector components on a graph. The script describes how to graphically represent each vector and then combine them to find the resultant.
πŸ’‘Resultant vector
A resultant vector is the single vector that represents the combined effect of multiple vectors acting together. The video's theme revolves around calculating this resultant vector by adding the individual displacement vectors. The script uses the term to describe the final vector obtained after adding the x and y components of the given vectors.
πŸ’‘Vector displacements
Vector displacements are directional movements from one point to another, represented as vectors with both magnitude and direction. The video script describes three vector displacements with specific magnitudes and angles, which are essential for determining the overall resultant vector.
πŸ’‘Degrees north of East
This phrase describes the direction of a vector in a coordinate system, specifically the angle measured from the East direction towards the North. The script uses this to specify the direction of each vector displacement, which is crucial for breaking down the vectors into their x and y components.
πŸ’‘Magnitude
In the context of vectors, magnitude refers to the length or size of the vector, which is the distance from the origin to the point represented by the vector on a graph. The video's main goal is to find the magnitude of the resultant vector, and the script explains how to calculate it using the x and y components.
πŸ’‘X and Y components
X and Y components are the horizontal and vertical parts of a vector when it is broken down in a two-dimensional coordinate system. The script explains how to calculate these components for each vector using trigonometric functions and then sum them up to find the resultant vector's components.
πŸ’‘Trigonometric functions
Trigonometric functions, such as cosine and sine, are mathematical functions that relate the angles of a triangle to the lengths of its sides. In the script, these functions are used to calculate the x and y components of each vector displacement from their magnitudes and angles.
πŸ’‘Significant figures
Significant figures are the digits in a number that carry meaning contributing to its precision. The script mentions rounding the components to two significant figures, which is a common practice in scientific calculations to ensure precision and readability.
πŸ’‘Hypotenuse
The hypotenuse is the longest side of a right-angled triangle, opposite the right angle. In the script, the magnitude of the resultant vector is found by calculating the hypotenuse of a right triangle formed by the x and y components.
πŸ’‘Square root
The square root of a number is a value that, when multiplied by itself, gives the original number. The script uses the square root to find the magnitude of the resultant vector by taking the square root of the sum of the squares of the x and y components.
Highlights

Graphically determine the magnitude of the resultant of three vector displacements.

Draw out the vectors graphically to understand the problem.

First vector is 150 meters at 30 degrees north of East.

Second vector is 220 meters at 37 degrees north of East.

Third vector is 25 meters at 45 degrees north of East.

Add up the components of the three vectors to find the resultant.

Use trigonometric functions to find x and y components of each vector.

For vector 1, calculate x component using cos(30) and y component using sin(30).

For vector 2, calculate x component using cos(37) and y component using sin(37).

For vector 3, calculate x and y components using cos(45) and sin(45).

Sum up the x and y components of all vectors to get net components.

Calculate the magnitude of the resultant vector using the net components.

Use the Pythagorean theorem to find the magnitude of the resultant vector.

The magnitude of the resultant vector is approximately 60 meters.

The graphical method provides an intuitive way to solve vector addition problems.

Trigonometric functions are essential for finding vector components.

The Pythagorean theorem is used to calculate the magnitude of a vector.

This problem demonstrates the practical application of vector addition and magnitude calculation.

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation #69

How To Find The Resultant of Two Vectors

AP Physics B Kinematics Presentation General Problems #08

AP Physics B Kinematics Presentation General Problems #09

AP Physics B Kinematics Presentation #47

Adding Vector Components | Physics with Professor Matt Anderson | M3-07

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Vector AnalysisGraphical SolutionDisplacementMagnitude CalculationTrigonometryResultant VectorNorth of EastMathematicsPhysicsEngineering