AP Physics B Kinematics Presentation #79

The New Jersey Center for Teaching and Learning
28 Jun 201204:51
EducationalLearning
32 Likes 10 Comments

TLDRThis script explores the physics of two objects, a horizontally thrown stone and a vertically dropped ball, both starting from the same height. It explains that despite the stone's initial horizontal velocity, both objects hit the ground at the same time due to the same vertical acceleration. The script then uses the Pythagorean theorem to demonstrate that the stone, with its horizontal velocity component, will have a greater overall velocity upon impact than the ball, which only has vertical velocity.

Takeaways
  • 🌍 A stone is thrown horizontally from the top of a tower at the same time a ball is dropped vertically.
  • 🏔️ The stone follows a parabolic path while the ball falls straight down.
  • 📝 Both objects start from the same height (H) and fall to the ground.
  • ⏱️ The time taken for both objects to hit the ground is the same.
  • 🔽 The final vertical velocity component for both objects is equal when they reach the ground.
  • 📐 The stone has an additional horizontal velocity component that the ball does not.
  • 📊 The resultant velocity of the stone is found using the Pythagorean theorem.
  • 💨 The stone’s final velocity is greater than the ball’s final velocity due to its horizontal component.
  • 📉 The vertical motion of both objects is independent of their horizontal motion.
  • 🚀 The stone travels faster than the ball when they both hit the ground.
Q & A

  • What is the scenario described in the script?

    -The script describes a scenario where a stone is thrown horizontally from the top of a tower at the same time a ball is dropped vertically from the same height. Both are aiming to hit the ground level below.

  • What is the initial horizontal velocity of the stone?

    -The initial horizontal velocity (Vx) of the stone has some value, but the script does not specify the exact number.

  • What is the initial vertical velocity of the stone and the ball?

    -The initial vertical velocity (Vy) of the stone is zero because it is thrown horizontally. For the ball, since it is dropped, its initial vertical velocity (Vy) is also zero.

  • What is the formula used to determine the time it takes for the objects to hit the ground?

    -The formula used is derived from the equation of motion: y = y_0 + v_y t + 1/2 a t^2. After canceling out terms, the time (T) is determined by T = sqrt(2y/a), where a is the acceleration due to gravity.

  • What is the acceleration due to gravity used in the script?

    -The acceleration due to gravity used in the script is 9.8 m/s^2.

  • Why is the time to hit the ground the same for both the stone and the ball?

    -The time to hit the ground is the same for both objects because they both start from rest and are only influenced by gravity, which acts equally on both.

  • How is the final vertical velocity of the stone and the ball determined?

    -The final vertical velocity is determined by the equation v_y = v_{y0} + a t. Since both objects start with an initial vertical velocity of zero, their final vertical velocity is the same and is determined by the time of fall and acceleration due to gravity.

  • What is the relationship between the final velocities of the stone and the ball when they hit the ground?

    -The final vertical component of the stone's velocity is the same as the ball's velocity. However, the stone also has a horizontal component of velocity, making its total velocity greater than the ball's when they hit the ground.

  • How is the total velocity of the stone calculated?

    -The total velocity of the stone is calculated using the Pythagorean theorem, where the total velocity (V) is the square root of the sum of the squares of the horizontal (Vx) and vertical (Vy) components of velocity.

  • Which object is traveling faster when it hits the ground, and why?

    -The stone is traveling faster when it hits the ground because, in addition to the same vertical velocity as the ball, it also has a horizontal component of velocity, resulting in a greater total velocity.

  • What is the significance of the Pythagorean theorem in this context?

    -The Pythagorean theorem is used to calculate the resultant velocity of the stone, which is the combination of its horizontal and vertical components of velocity, to determine its total speed upon impact with the ground.

Outlines
00:00
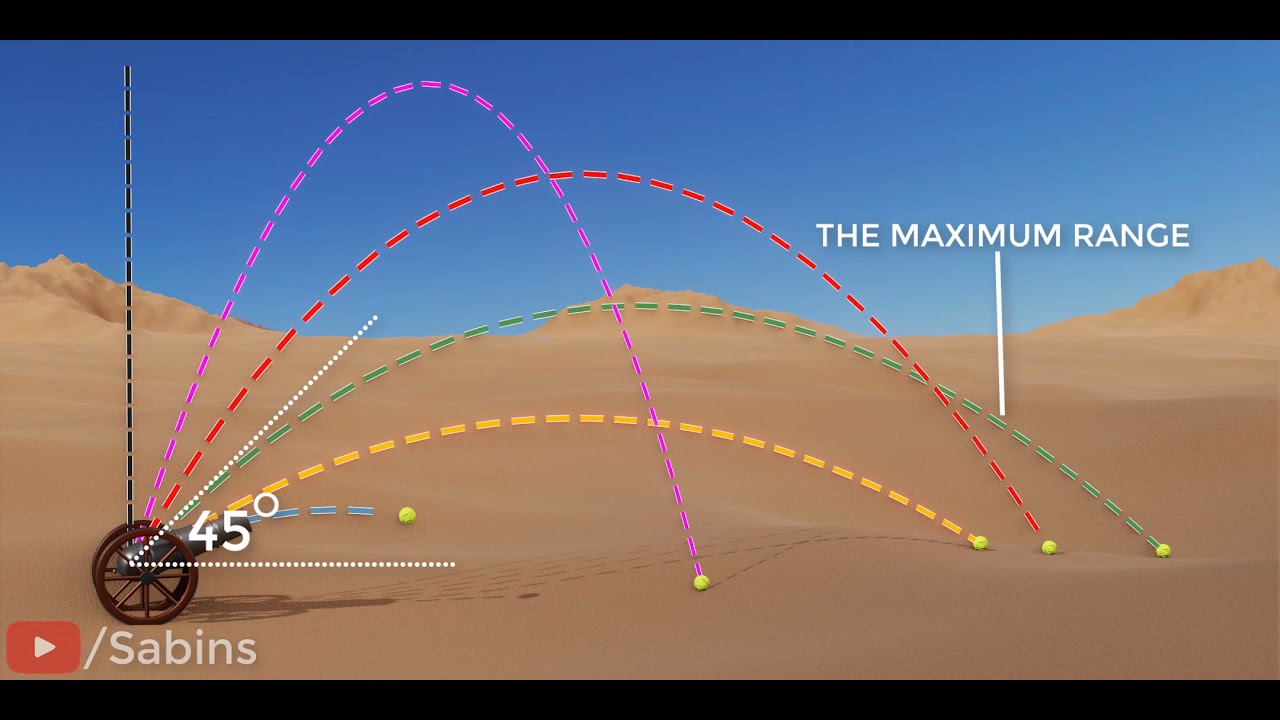
📚 Horizontal vs Vertical Projectile Motion

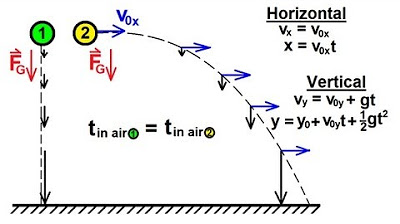
This paragraph discusses a physics problem involving a stone thrown horizontally from the top of a tower and a ball dropped vertically from the same height. The main question is which object will be traveling faster when it hits the ground. The scenario is visualized with a drawing that includes the ground level, the cliff or tower, and the trajectories of the stone and the ball. Initial velocities for both objects are given, with the stone having a horizontal velocity and the ball having none. The focus then shifts to calculating the time it takes for each object to reach the ground, using the equation of motion under gravity. The conclusion is that both objects take the same amount of time to fall, but the stone, having a horizontal component of velocity in addition to the vertical, will have a greater resultant velocity upon impact.

Mindmap
Keywords
💡Projectile Motion
Projectile motion is a form of motion experienced by an object or particle that is thrown near the Earth's surface and moves along a curved path under the action of gravity only. In the video, the stone is thrown horizontally, exhibiting projectile motion with a parabolic trajectory, which is a key concept in understanding the dynamics of the problem presented.
💡Free Fall
Free fall is the motion of an object under the sole influence of gravity, starting from an initial velocity of zero. The ball in the video is dropped vertically, undergoing free fall, which is a fundamental concept in the study of motion and gravity, and it contrasts with the projectile motion of the stone.
💡Velocity Components
Velocity components refer to the individual velocities of an object in different directions when it is moving in a plane. In the script, the stone has a horizontal component (Vx) and a vertical component (Vy), while the ball only has a vertical component due to gravity. Understanding these components is crucial for analyzing the motion of both objects.
💡Initial Velocity
Initial velocity is the speed of an object at the start of its motion. The stone has an initial horizontal velocity (Vx), while the ball has none, as it is dropped. This concept is important for determining the trajectory and speed of the stone as it moves through the air.
💡Acceleration Due to Gravity
Acceleration due to gravity, often denoted as 'g', is the acceleration that an object experiences when it is in free fall. In the script, it is used to calculate the time it takes for both the stone and the ball to reach the ground, with a value of 9.8 m/s² on Earth's surface.
💡Time of Flight
Time of flight is the time taken by an object in projectile motion to reach the ground. The script calculates the time it takes for both the stone and the ball to fall to the ground using the formula derived from the equations of motion, which is essential for comparing their speeds at impact.
💡Final Velocity
Final velocity is the speed of an object at the end of its motion. The script explains that both the stone and the ball will have the same final vertical velocity (Vy) when they hit the ground due to the acceleration due to gravity, but the stone will have an additional horizontal component.
💡Pythagorean Theorem
The Pythagorean theorem is used to calculate the resultant velocity of the stone by combining its horizontal and vertical velocity components. The theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides, which is applied in the script to find the magnitude of the stone's velocity at impact.
💡Resultant Velocity
Resultant velocity is the overall velocity of an object when it has components of motion in different directions. The script uses the Pythagorean theorem to find the resultant velocity of the stone, which is greater than the velocity of the ball due to its horizontal component.
💡Hypotenuse
In the context of the video, the hypotenuse is the diagonal of a right-angled triangle that represents the resultant velocity of the stone. The script uses the Pythagorean theorem to calculate the hypotenuse, which corresponds to the magnitude of the stone's velocity as it hits the ground.
Highlights

A stone is thrown horizontally and a ball is dropped vertically from the same height at the same time.

The problem explores which object is traveling faster when it hits the ground.

A conceptual diagram is drawn to visualize the parabolic motion of the stone and the vertical fall of the ball.

Initial velocities are given for the stone (VX has a value, VY is zero) and the ball (VX is zero, VY is zero).

Both objects start from an initial height H and reach a final height of 0 upon hitting the ground.

The equation y = y + vy*t + 1/2*a*t^2 is simplified to solve for the time of fall.

Time taken for both the stone and the ball to fall to the ground is found to be the same.

The final vertical velocity of both objects is determined to be the same due to initial vertical velocities being zero.

The stone has an additional horizontal component of velocity, which the ball lacks.

The Pythagorean theorem is used to calculate the resultant velocity of the stone.

The stone's velocity is the vector sum of its horizontal and vertical components.

The ball's velocity is purely vertical, as it was dropped without horizontal motion.

The stone's resultant velocity is greater than the ball's vertical velocity.

The conclusion is that the stone will hit the ground traveling faster than the ball.

The problem demonstrates the principles of projectile motion and the effects of initial horizontal velocity.

The analysis shows the importance of considering both horizontal and vertical components of velocity in projectile motion.

The transcript provides a clear explanation of the physics behind the motion of objects thrown and dropped from a height.

Transcripts

Browse More Related Video

introduction to projectile motion

The Classic Bullet Projectile Motion Experiment

Physics 3: Motion in 2-D Projectile Motion (1 of 21) Independent Motion in x and y

Solving Projectile Motion Problems in Physics - [1-4-7]

2015 AP Physics 1 Free Response #4

AP Physics B Kinematics Presentation #77

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Projectile MotionPhysicsHorizontal ThrowVertical DropParabolic PathVelocity ComparisonFree FallTerminal VelocityMotion AnalysisSpeed CalculationPhysics Education