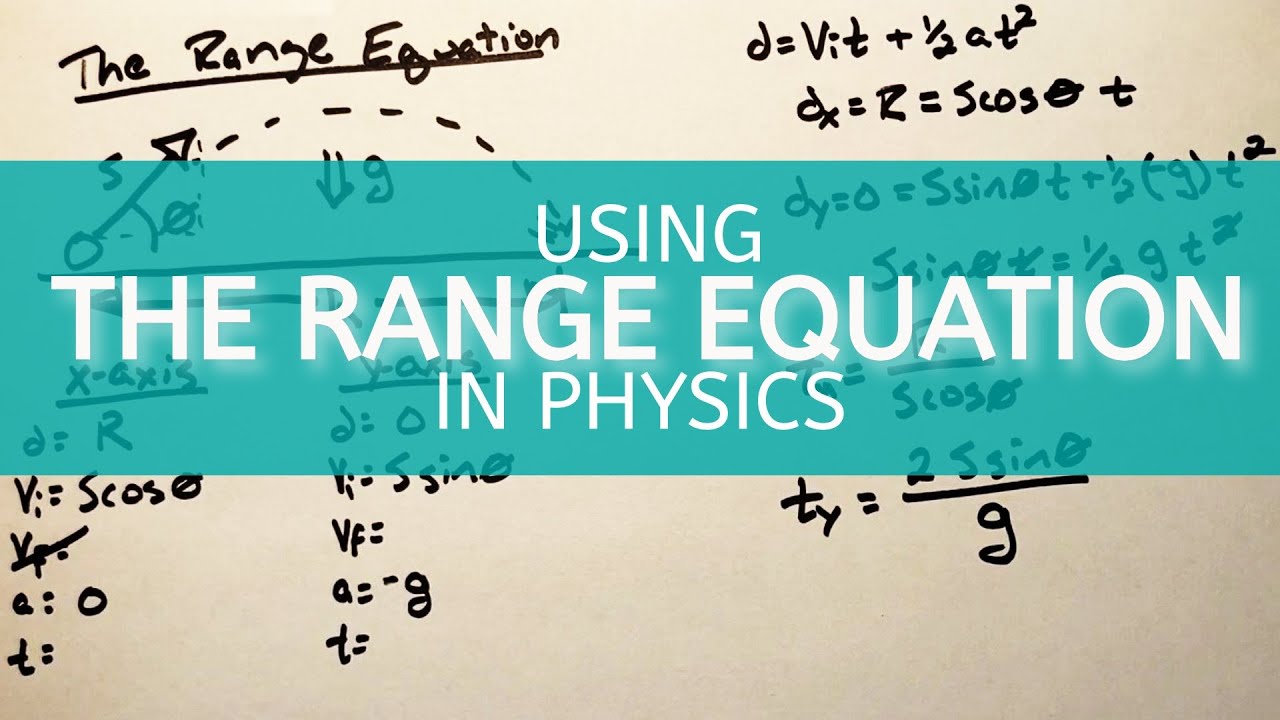AP Physics B Kinematics Presentation #74
TLDRThe video explains the optimal angle for a water gun to achieve the greatest horizontal range. It starts by detailing the projectile motion of the water stream, leading to the derivation of the range equation: R = (V^2 * sin(2θ)) / g. By analyzing the components of motion and applying trigonometric identities, it concludes that the angle θ should be 45 degrees. This angle maximizes the sine function value to 1, thus achieving the greatest horizontal range for the water gun.
Takeaways
- 🔍 The script discusses the optimal angle for a water gun to achieve the greatest horizontal range in projectile motion.
- 📐 It starts by considering the vertical component of motion, using the initial velocity in the Y direction and gravity to calculate the time of flight.
- ⏱ The time of flight is derived from the equation of motion, considering the initial and final positions in the Y direction to be zero.
- 🌡 The acceleration due to gravity is constant at -9.8 m/s², which is used to find the time it takes for the water to reach its maximum height and fall back to the ground.
- 🔄 The horizontal range (R) is then calculated using the horizontal component of the initial velocity and the time of flight.
- 📉 The equation for range is simplified to R = V₀² sin(2θ) / G, where V₀ is the initial velocity, θ is the angle, and G is the acceleration due to gravity.
- 📚 Trigonometric identities are used to show that 2 sin(θ) cos(θ) is equivalent to sin(2θ), which is crucial for the range equation.
- 📈 To maximize the range, the sine of 2θ must be maximized, which occurs when its value is 1, within the range of 0 to 90 degrees for the angle θ.
- 🧭 The angle that results in sin(2θ) = 1 is found by taking the inverse sine of 1, which corresponds to an angle of 45 degrees.
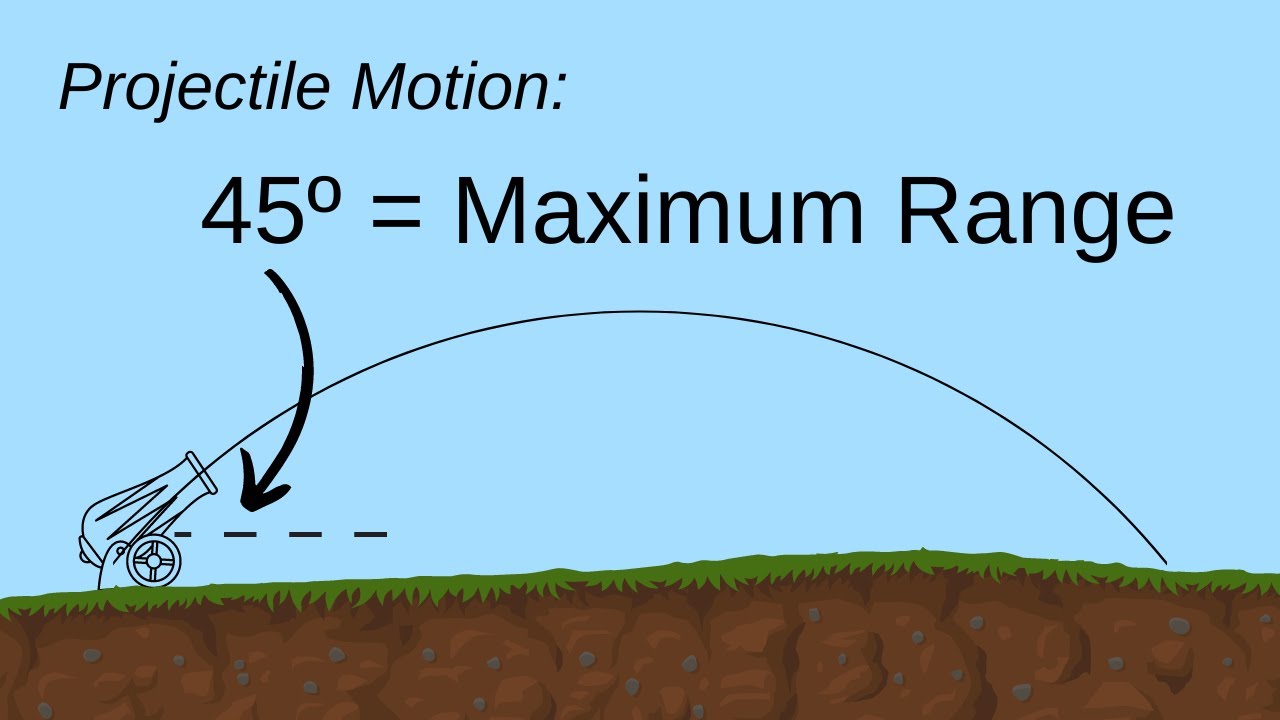
- 🎯 The conclusion is that to achieve the greatest horizontal range, the water gun should be aimed at a 45-degree angle.
- 📝 The script provides a clear explanation of the physics behind projectile motion and how to calculate the optimal firing angle for maximum range.
Q & A
What is the main topic discussed in the script?
-The main topic discussed in the script is the optimal angle to aim a water gun to achieve the greatest horizontal range in projectile motion.
What is the formula given for the range (R) of a projectile in the script?
-The formula given for the range (R) of a projectile is R = V^2 * sin(2θ) / G, where V is the initial velocity, θ is the angle of projection, and G is the acceleration due to gravity.
Why is the sine of two theta (sin(2θ)) used in the formula?
-The sine of two theta (sin(2θ)) is used because it is derived from the trigonometric identity sin(2θ) = 2 * sin(θ) * cos(θ), which simplifies the expression for the range of the projectile.
What is the significance of the angle θ in the formula?
-The angle θ is significant because it determines the direction of the projectile's launch, and it affects the range achieved by the projectile.
What is the maximum value that sin(2θ) can achieve?
-The maximum value that sin(2θ) can achieve is 1, which occurs when the angle 2θ is 90 degrees.
What angle should the water gun be aimed at to maximize the range?
-The water gun should be aimed at an angle of 45 degrees to maximize the range, as this is when sin(2θ) equals 1.
What is the initial velocity component in the Y direction?
-The initial velocity component in the Y direction is V₀ * sin(θ), where V₀ is the initial velocity and θ is the angle of projection.
What is the acceleration acting on the projectile in the Y direction?
-The acceleration acting on the projectile in the Y direction is -G, where G is the acceleration due to gravity (9.8 m/s²).
How is the time of flight of the projectile calculated in the script?
-The time of flight is calculated using the formula T = 2 * V₀ * sin(θ) / G, which is derived from the equation of motion for the Y component.
How does the horizontal range (X) of the projectile relate to the time of flight?
-The horizontal range (X) is directly proportional to the time of flight, as X = V₀ * cos(θ) * T, where T is the time of flight.
What is the initial and final position of the Y component in the script's context?
-In the script's context, the initial and final position of the Y component is zero meters, indicating that the projectile starts and lands at the same height.
Outlines
💧 Understanding Projectile Motion for Maximum Range
This paragraph delves into the physics of projectile motion, specifically how to achieve the greatest horizontal range with a water gun. The script explains the importance of the angle of projection, denoted as theta, and how it affects the parabolic trajectory of the water stream. The equation R = (V₀² * sin(2θ)) / G is introduced, where R is the range, V₀ is the initial velocity, G is the acceleration due to gravity, and θ is the angle of projection. The explanation involves breaking down the motion into Y and X components, solving for time, and then using trigonometric identities to derive the formula for maximum range. The focus is on understanding the mathematical derivation and the significance of each variable in the equation.
🎯 Maximizing Range by Optimal Angle Selection
The second paragraph focuses on maximizing the range of the water gun's stream by finding the optimal angle of projection. It explains that to achieve the maximum range, one must maximize the sine of 2θ in the equation R = V₀² * sin(2θ) / G, given that the initial velocity and gravitational acceleration are constants. The sine function reaches its maximum value of 1 at 90 degrees, but since the angle is doubled in the equation, the optimal angle θ is found to be 45 degrees. This is derived by setting sin(2θ) to 1 and solving for θ, which results in θ = 45°. The conclusion is that firing the water gun at a 45-degree angle will yield the greatest horizontal range, and the answer to the question is provided as 45 degrees.
Mindmap
Keywords
💡Projectile Motion
💡Parabolic Path
💡Angle of Projection
💡Horizontal Range
💡Initial Velocity
💡Trigonometric Identities
💡Sine Function
💡Cosine Function
💡Acceleration Due to Gravity
💡Maximization
💡45 Degrees
Highlights
The water gun should be aimed at an angle for maximum horizontal range.
Projectile motion is described along the ground with a parabolic path.
The equation R = V^2 * sin(2θ) / G is derived from the projectile motion.
The Y-component of motion is analyzed with initial and final positions set to zero.
Initial velocity in the Y direction is V₀ * sin(θ).
Acceleration due to gravity is represented as -G, where G is 9.8 m/s².
Time of flight is calculated using the equation 2 * V₀ * sin(θ) / G.
The X-component of motion is related to the range (R) and initial velocity in the X direction (V₀ * cos(θ)).
The time for the object to travel from its initial to final Y position is used in the X equation.
The range (R) is expressed as V₀² * 2 * sin(θ) * cos(θ) / G.
Trigonometric identity sin(2θ) = 2 * sin(θ) * cos(θ) is applied to simplify the range equation.
The goal is to maximize the range R by maximizing sin(2θ).
The sine function has a range between 0 and 1, with 1 being the maximum value.
The angle that makes sin(2θ) equal to 1 is found by taking the inverse sine of 1.
The angle θ that results in the maximum range is 45 degrees.
To achieve the greatest horizontal range, the water gun should be fired at a 45-degree angle.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: