AP Physics B Kinematics Presentation #82

The New Jersey Center for Teaching and Learning
26 Jun 201203:15
EducationalLearning
32 Likes 10 Comments

TLDRThis script explores the physics of projectile motion, focusing on achieving the same horizontal range with different launch angles. It uses the formula x = (v^2 * sin(2θ)) / G to demonstrate that launching a projectile at 30° or 60° with the same initial velocity and gravity will result in the same range. The script methodically eliminates other angles, confirming that 30° is the correct answer for achieving equivalent horizontal distance as the initial 60° launch.

Takeaways
  • 🚀 The script discusses the concept of a projectile launched at an angle with a given initial velocity.
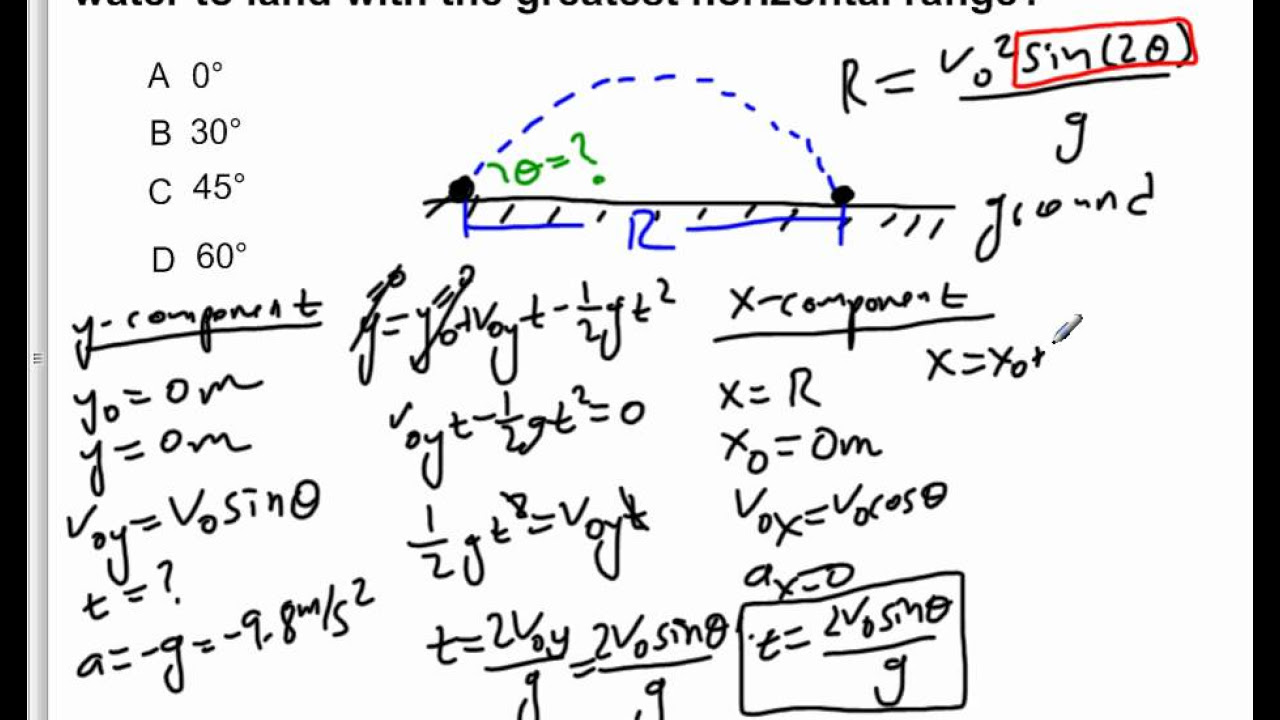
  • 📚 The horizontal range of a projectile is determined by the equation \( x = \frac{v^2 \sin(2\Theta)}{G} \), where \( v \) is the initial velocity, \( \Theta \) is the launch angle, and \( G \) is the acceleration due to gravity.
  • 🔍 The initial launch angle in the example is 60°, and the goal is to find another angle that results in the same horizontal range.
  • 🧭 The script mentions that the sine of double the angle (sin(2*Theta)) is crucial for determining the horizontal range.
  • 📉 The script calculates the sine values for different angles to find the one that matches the horizontal range of the 60° launch.
  • 🔢 For a 20° launch angle, the script calculates the sine of 40°, which results in a different horizontal range.
  • 🎯 At a 30° launch angle, the script finds that the sine of 60° matches the original horizontal range, indicating a potential correct answer.
  • 🔄 The script continues to check other angles such as 40°, 45°, and 50° to ensure that 30° is indeed the unique solution.
  • 📌 The sine of 80° for a 40° launch angle and sine of 100° for a 50° launch angle both result in different horizontal ranges.
  • 🏁 The script concludes that launching the projectile at 30° will yield the same horizontal range as the initial 60° launch, given the constant velocity and gravity.
  • 📝 The final answer provided in the script is B 30°, which is the angle that results in the same horizontal range as the initial 60° launch.
Q & A

  • What is the initial angle at which the projectile is fired in the first trial?

    -The projectile is fired at an initial angle of 60° above the horizontal line.

  • What is the formula for the horizontal range of a projectile?

    -The horizontal range of a projectile is given by the equation \( x = \frac{v^2 \sin(2\Theta)}{G} \), where \( v \) is the initial velocity, \( \Theta \) is the launch angle, and \( G \) is the acceleration due to gravity.

  • Why is the horizontal range the same for the first trial and the other cases?

    -The horizontal range is the same for the first trial and the other cases because the initial velocity \( v \) and acceleration due to gravity \( G \) are constant for all trials.

  • What is the significance of the equation \( \sin(2\Theta) \) in the range formula?

    -The \( \sin(2\Theta) \) term in the range formula represents the component of the initial velocity that contributes to the horizontal displacement of the projectile.

  • What is the value of the horizontal range for the first trial?

    -The value of the horizontal range for the first trial is 866 units, as calculated from the given initial velocity and launch angle.

  • What is the relationship between the launch angle and the horizontal range?

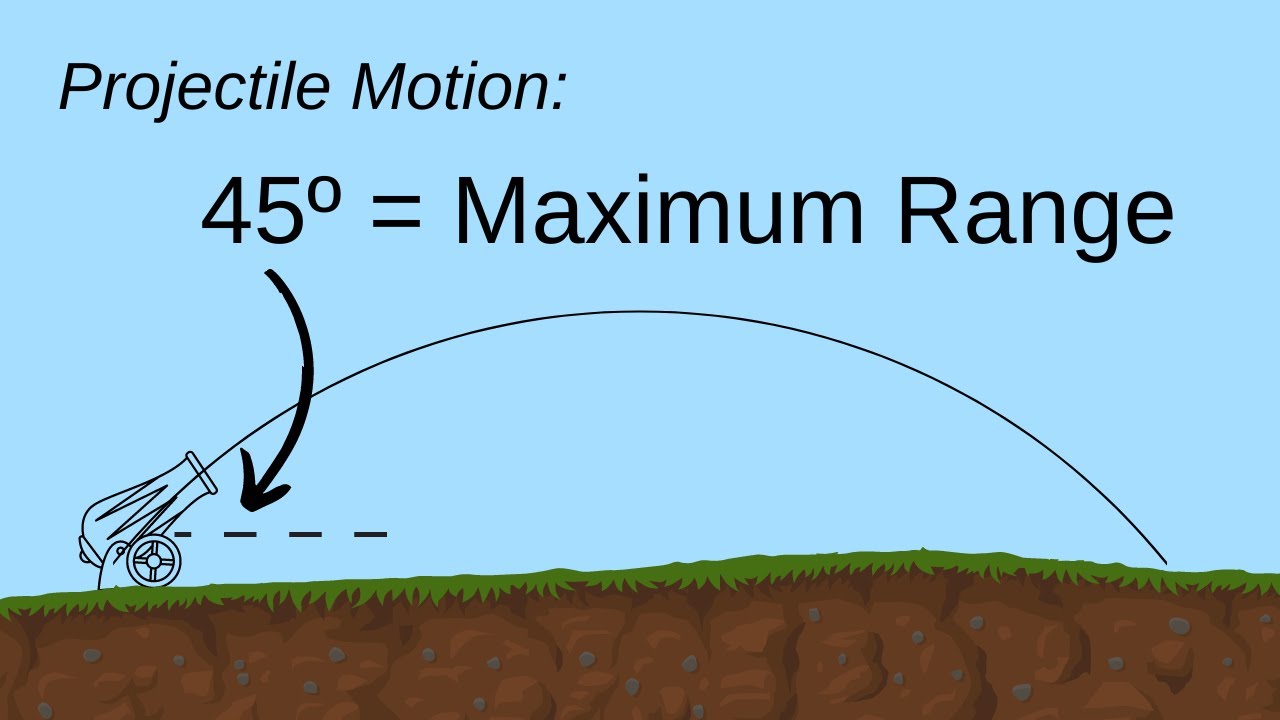
    -The horizontal range is maximized when the launch angle is such that \( \sin(2\Theta) \) is maximized, which occurs at an angle of 45° for the standard projectile motion equations.

  • Why is the angle of 30° considered in the script?

    -The angle of 30° is considered because when doubled, it results in 60°, which is the same as the initial launch angle in the first trial, potentially leading to the same horizontal range.

  • What is the value of the horizontal range when the launch angle is 30°?

    -When the launch angle is 30°, the horizontal range is also 866 units, which matches the range of the first trial.

  • What happens to the horizontal range as the launch angle increases from 30° to 45° and beyond?

    -The horizontal range increases as the launch angle approaches 45°, reaching a maximum, and then decreases as the angle goes beyond 45°.

  • What is the conclusion of the script regarding the launch angle that results in the same horizontal range as the first trial?

    -The conclusion of the script is that firing the projectile at a 30° angle will result in the same horizontal range as the first trial, given the constant initial velocity and acceleration due to gravity.

Outlines
00:00
🚀 Projectile Motion Analysis

This paragraph discusses the principles of projectile motion, specifically focusing on the horizontal range of a projectile launched at an angle. It explains that the range is determined by the initial velocity (V), the angle of launch (Theta), and the acceleration due to gravity (G). The formula for horizontal range, x = (V^2 * sin(2Theta)) / G, is introduced. The paragraph then explores the scenario of firing a projectile at 60° and seeks to find other angles that would result in the same horizontal range, using the sine function's property that sin(2Theta) = sin(180° - 2Theta). The analysis concludes that launching the projectile at 30° would yield the same horizontal range as at 60°, given the constants V and G.

Mindmap
Keywords
💡Projectile
A projectile is an object that is given an initial velocity and moves along a curved path under the action of gravity. In the context of the video, the term refers to an object launched at an angle above the horizontal. The script discusses how the projectile's range is affected by the angle of launch and initial velocity, illustrating the physics of projectile motion.
💡Horizontal Line
A horizontal line is a straight line parallel to the ground or the base of a reference frame. In the video script, the horizontal line serves as the baseline from which the angle of the projectile's launch is measured. It is essential for understanding the trajectory and range of the projectile.
💡Initial Velocity (V)
Initial velocity is the speed at which an object starts moving. In the script, the initial velocity 'V' is a constant value for the projectile's launch. It is a critical factor in determining the range and trajectory of the projectile, as it directly influences the distance the projectile will travel.
💡Angle of Launch
The angle of launch is the angle between the initial velocity vector of the projectile and the horizontal line. In the video, the angle of 60° is initially used, and the script explores how changing this angle affects the horizontal range of the projectile.
💡Horizontal Range
Horizontal range refers to the distance a projectile travels in the horizontal direction before landing. The script uses the equation 'x = v^2 sin(2Theta) / G' to calculate the horizontal range, emphasizing its dependence on the launch angle and initial velocity.
💡Equation
In the context of the video, the equation 'x = v^2 sin(2Theta) / G' is used to determine the horizontal range of a projectile. It is a mathematical representation that combines the concepts of initial velocity, launch angle, and gravity to predict the projectile's behavior.
💡Sine Function (sin)
The sine function is a trigonometric function that relates the ratio of the length of the opposite side to the hypotenuse in a right-angled triangle. In the script, 'sin(2Theta)' is used within the equation to calculate the horizontal range, showing the relationship between the launch angle and the distance traveled.
💡Acceleration Due to Gravity (G)
Acceleration due to gravity is the acceleration that an object experiences due to the gravitational pull of the Earth. In the video, 'G' is a constant that affects the projectile's trajectory by pulling it downward, and it is a factor in the range equation.
💡Theta
Theta (Θ) is a symbol often used to denote an angle in trigonometry. In the script, 'Theta' represents the launch angle of the projectile, and the script explores different values of 'Theta' to find which ones yield the same horizontal range as the initial 60° launch.
💡Calculation
Calculation in this context refers to the process of using the provided equation to determine the horizontal range of the projectile for different launch angles. The script demonstrates calculations for various angles to find the one that matches the initial range.
💡Answer Choices
Answer choices are the possible options provided in the script to determine the correct launch angle that will result in the same horizontal range as the initial launch. The script evaluates each choice mathematically to identify the correct angle, which is found to be 30°.
Highlights

A projectile is fired at 60° above the horizontal line with an initial velocity V.

The horizontal range of a projectile is given by the equation x = v^2 * sin(2 * θ) / g.

We need to find the angle at which the projectile will land the same distance away as in the first trial.

For all cases, we launch with the same initial velocity V and acceleration due to gravity g.

The only factor dictating the horizontal range is the launch angle.

The sine of 2 * 60° is equivalent to the sine of 120°, which equals 0.866.

We need to find another angle that results in a sine value of 0.866.

Calculating for 20°, the sine of 40° equals 0.642.

Calculating for 30°, the sine of 60° equals 0.866.

30° matches the value needed for the same horizontal range.

Calculating for 40°, the sine of 80° equals 0.984.

Calculating for 45°, the sine of 90° equals 1.

Calculating for 50°, the sine of 100° equals 0.984.

The only angle that results in the same horizontal range is 30°.

The answer is B, 30°, because it produces the same range as 60°.

Transcripts

Browse More Related Video

Understanding the Range Equation of Projectile Motion

Why Does 45º Launch Angle Give Maximum Range? // HSC Physics

Where Does The Range Equation Come From?

AP Physics B Kinematics Presentation #74

AP Physics B Kinematics Presentation General Problems #11

Consolidation: Projectile Motion Calculations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Projectile MotionPhysicsMathematicsLaunch AngleHorizontal RangeVelocityGravityCalculationScienceEducation