Other Indeterminate Forms

RH Mathematics
1 Nov 202112:34
EducationalLearning
32 Likes 10 Comments

TLDRThis video explores indeterminate forms in calculus, specifically using L'Hôpital's Rule to solve complex limits involving infinity and zero. Examples include infinity minus infinity, infinity times zero, and one to the power of infinity. The presenter demonstrates algebraic manipulation and derivative calculations to find the limits, highlighting the importance of understanding these forms in advanced calculus.

Takeaways
  • 📚 The video discusses indeterminate forms and the use of L'Hôpital's Rule for solving limits that are not typically covered in AP Calculus.
  • 🔍 It clarifies common misconceptions about indeterminate forms, such as infinity minus infinity and infinity to the power of zero.
  • 📉 The script provides an example of an 'infinity minus infinity' limit, showing that it can lead to a determinate value, in this case, 1/2, contrary to the common belief that it equals zero.
  • 🔄 The presenter demonstrates the process of using L'Hôpital's Rule by taking derivatives of the numerator and denominator to resolve indeterminate forms like 0/0.
  • 📝 The video emphasizes the importance of algebraic manipulation and finding a common denominator to simplify expressions before applying L'Hôpital's Rule.
  • 🧩 The presenter makes a mistake and corrects it during the explanation, showing the iterative process of problem-solving in calculus.
  • 🌐 An 'infinity times zero' limit is explored, and it's shown that by rewriting the expression, L'Hôpital's Rule can be applied, leading to a determinate result of 1.
  • 📈 The video covers a 'one to the infinity' limit, illustrating how logarithms can be used to transform and solve such indeterminate forms.
  • 🔑 The use of logarithmic properties simplifies the 'one to the infinity' limit problem, eventually leading to the discovery that the limit equals 'e', the base of natural logarithms.
  • 🤓 The video concludes with a reminder of the definition of 'e' and its significance in calculus, emphasizing the practical application of theoretical concepts.
  • 📚 The overall message is that while indeterminate forms can be complex, with the right approach and tools, such as L'Hôpital's Rule and algebraic manipulation, they can be resolved to find determinate limits.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is discussing indeterminate forms and using L'Hôpital's rule to solve calculus problems that are not typically seen in AP Calculus.

  • What are indeterminate forms in calculus?

    -Indeterminate forms in calculus are expressions that cannot be simplified to a determinate value using the standard rules of algebra but can often be resolved using calculus techniques such as L'Hôpital's rule.

  • Why is infinity minus infinity not always zero?

    -Infinity minus infinity is not always zero because it depends on the context and the functions involved. The video shows an example where infinity minus infinity approaches a half.

  • What is the significance of zero over zero in calculus?

    -Zero over zero is an indeterminate form, which means that the limit may not be immediately clear and requires further analysis, often using L'Hôpital's rule or other calculus techniques.

  • Why does the video mention infinity to the power of zero?

    -The video mentions infinity to the power of zero to illustrate that it is not always equal to one, contrary to a common misconception, and it can be another form of an indeterminate form.

  • How does the video approach the problem of infinity minus infinity?

    -The video approaches the problem by finding a common denominator and then applying L'Hôpital's rule to resolve the indeterminate form.

  • What is L'Hôpital's rule used for?

    -L'Hôpital's rule is used for finding the limit of a quotient of two functions when the limit is of the form zero over zero or infinity over infinity.

  • What is the example given in the video for an infinity times zero limit?

    -The video provides an example of sine of 1 over x as x approaches infinity, which initially appears as an infinity times zero limit but is rewritten to apply L'Hôpital's rule.

  • How does the video handle the one to the infinity limit?

    -The video uses logarithms to transform the one to the infinity limit into an indeterminate form of zero over zero, which can then be solved using L'Hôpital's rule.

  • What is the final result of the one to the infinity limit example in the video?

    -The final result of the one to the infinity limit example is that it equals e, which is the base of the natural logarithm.

  • What is the importance of the definition of e in the context of the video?

    -The definition of e is important because it is derived from a limit involving one to the power of infinity, which is a concept discussed in the video.

Outlines
00:00
📚 Introduction to Indeterminate Forms and L'Hôpital's Rule

The video begins with an introduction to indeterminate forms, particularly focusing on scenarios not commonly covered in AP Calculus. The host aims to clarify misconceptions about expressions like infinity minus infinity and infinity to the power of zero. The video promises to delve into these forms using L'Hôpital's Rule, starting with an example of infinity minus infinity, which simplifies to a zero over zero limit. The host demonstrates the process of finding a common denominator and applying L'Hôpital's Rule, emphasizing the importance of algebraic manipulation in solving such limits.

05:02
🔍 Exploring Infinity Minus Infinity and Infinity Times Zero

This paragraph explores the indeterminate forms of infinity minus infinity and infinity times zero. The host provides an example of infinity minus infinity, which surprisingly approaches a non-zero value, specifically 1/2, after applying L'Hôpital's Rule. The infinity times zero scenario is also discussed, where the sine function is used to transform the problem into a zero over zero form, allowing the use of L'Hôpital's Rule. The host shows that in this case, the limit approaches 1, contrary to the common assumption that infinity times zero equals zero.

10:03
🌟 One to the Power of Infinity and the Natural Logarithm Approach

The final paragraph tackles the one to the power of infinity limit, a complex scenario where the base approaches one and the exponent approaches infinity. The host uses logarithms to transform the equation and then applies L'Hôpital's Rule to find the limit. The process involves recognizing the 0/0 indeterminate form and using the properties of logarithms to simplify the expression. The host concludes by solving for 'w', revealing it to be 'e', which ties back to the definition of the mathematical constant 'e' as the limit of (1 + 1/n)^n as n approaches infinity.

Mindmap
Keywords
💡Indeterminate Forms
Indeterminate forms are expressions that initially appear to have no determinate value, such as 0/0 or ∞/∞, but can be resolved through mathematical techniques. In the video, the theme revolves around these forms, particularly how they appear in calculus problems and how they can be tackled using L'Hôpital's Rule or other methods.
💡L'Hôpital's Rule
L'Hôpital's Rule is a mathematical technique used to evaluate limits of indeterminate forms by taking the derivatives of the numerator and denominator. The video script provides examples of applying this rule to solve complex limits, such as ∞ - ∞ and 1^∞, showcasing its utility in calculus.
💡Infinity
Infinity is a concept that represents an unbounded quantity, larger than any number. In the context of the video, infinity is used to describe certain limits, such as when a function's value grows without bound. The script discusses indeterminate forms involving infinity, like ∞ - ∞ and ∞ * 0.
💡Zero Over Zero
Zero over zero is an indeterminate form where both the numerator and the denominator approach zero. The video explains that this form does not necessarily equate to one, contrary to the common misconception, and demonstrates how to resolve it using calculus.
💡Common Denominator
A common denominator is a single value that can be used as the denominator for multiple fractions, allowing for their combination or comparison. In the script, the presenter uses a common denominator to simplify expressions involving infinity and to apply L'Hôpital's Rule.
💡Derivative
The derivative in calculus represents the rate at which a function changes with respect to its variable. The video script frequently mentions taking derivatives, which is a key step in applying L'Hôpital's Rule to evaluate limits.
💡Natural Logarithm
The natural logarithm, often denoted as ln(x), is the logarithm to the base e. The video uses natural logarithms to transform and simplify expressions, particularly in the context of limits involving exponential growth or decay.
💡Limit
A limit in calculus is the value that a function or sequence approaches as the input approaches some value. The video's main theme is evaluating limits, especially those that are indeterminate, using various mathematical techniques.
💡Algebraic Manipulation
Algebraic manipulation refers to the process of rearranging and combining algebraic expressions to simplify them or to make them more amenable to further analysis. The script describes several instances where algebraic manipulation is used to transform indeterminate forms into a form that can be evaluated.
💡Euler's Number (e)
Euler's number, denoted as e, is an important mathematical constant approximately equal to 2.71828. It is the base of the natural logarithm. The video concludes with an example that defines e as the limit of (1 + 1/n)^n as n approaches infinity, illustrating its significance in calculus.
Highlights

Introduction to indeterminate forms and the use of L'Hôpital's rule.

Discussion on the common misconceptions about infinity and its operations.

Explaining why infinity minus infinity is not zero.

Demonstration of using common denominators to simplify expressions.

Application of L'Hôpital's rule to solve 0/0 limits.

Derivation process of x log x and its simplification.

Use of algebraic manipulation to clear out unnecessary terms in the expression.

Reiteration of L'Hôpital's rule for solving indeterminate forms.

Example of infinity minus infinity resulting in a non-zero value.

Introduction to infinity times zero limit and its indeterminate form.

Rewriting expressions using division to apply L'Hôpital's rule.

Derivation of cosine and its properties in the context of limits.

Demonstration of how infinity times zero can result in a non-zero value.

Introduction to one to the infinity limit and its algebraic manipulation.

Use of natural logarithms to transform and solve complex limits.

Application of logarithmic properties to simplify expressions in limits.

Final solution of the one to the infinity limit using L'Hôpital's rule.

Conclusion on the value of e and its relation to the limit of (1 + 1/x)^x as x approaches zero.

Transcripts

Browse More Related Video

Using L'Hopital's Rule to show that exponentials dominate polynomials

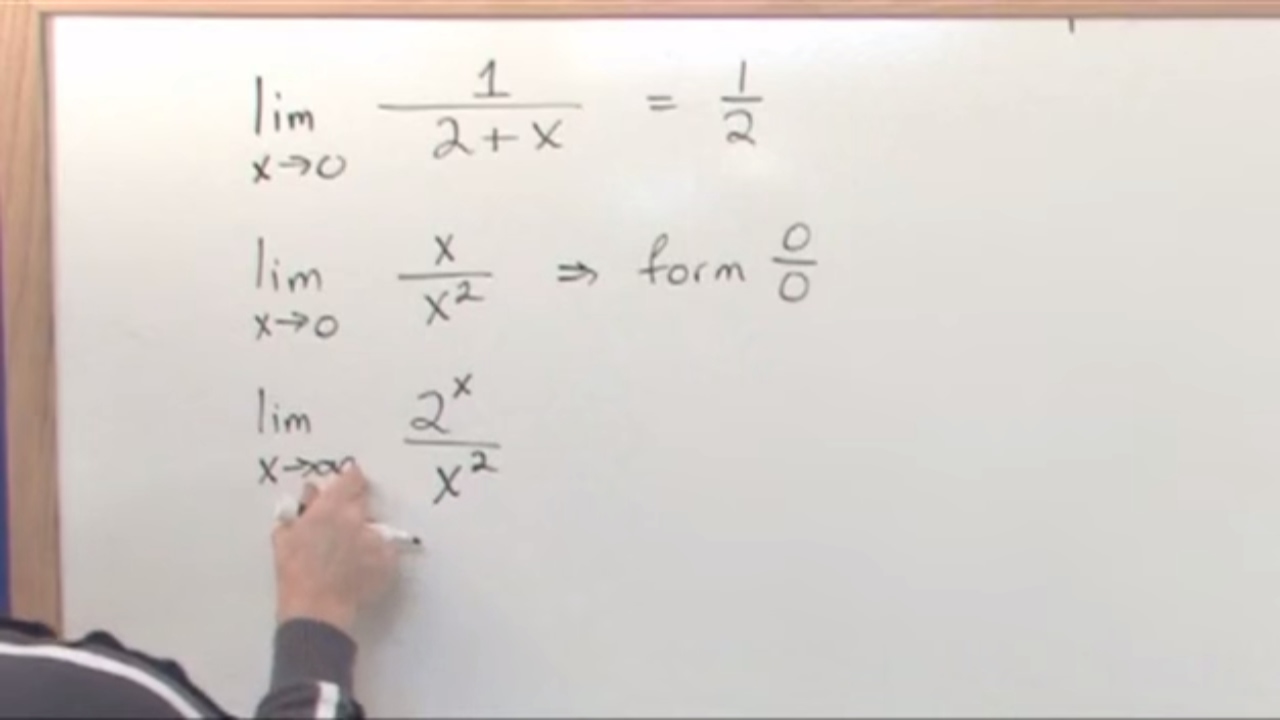
Lesson 5 - L'hopitals Rule (Calculus 2 Tutor)

Calculus AB Homework 4.3: L'Hospital's Rule

Example of Using L'Hopital's Rule Twice to Evaluate a Limit

Introduction to l'Hôpital's rule | Derivative applications | Differential Calculus | Khan Academy

Limit of x! over x^x as x goes to infinity

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusIndeterminate FormsL'Hôpital's RuleEducational ContentAdvanced MathLimit ProblemsInfinity ConceptsZero OverZeroInfinite SeriesMathematics TutorialAP Calculus