EMF & flux equation (& graph) of AC generator | Electromagnetic induction | Physics | Khan Academy
TLDRThis video explores the relationship between voltage and magnetic flux in a spinning coil. It explains Faraday's law, demonstrating how changing magnetic flux induces voltage. The video builds an equation for voltage, plots flux and induced emf over time, and highlights the alternating nature of the voltage, emphasizing the importance of flux change rather than flux itself.
Takeaways
- 🌀 Spinning a coil in a magnetic field induces a voltage, which can be used to power electrical devices.
- 📈 The voltage generated is dependent on the change in magnetic flux through the coil over time, as described by Faraday's Law.
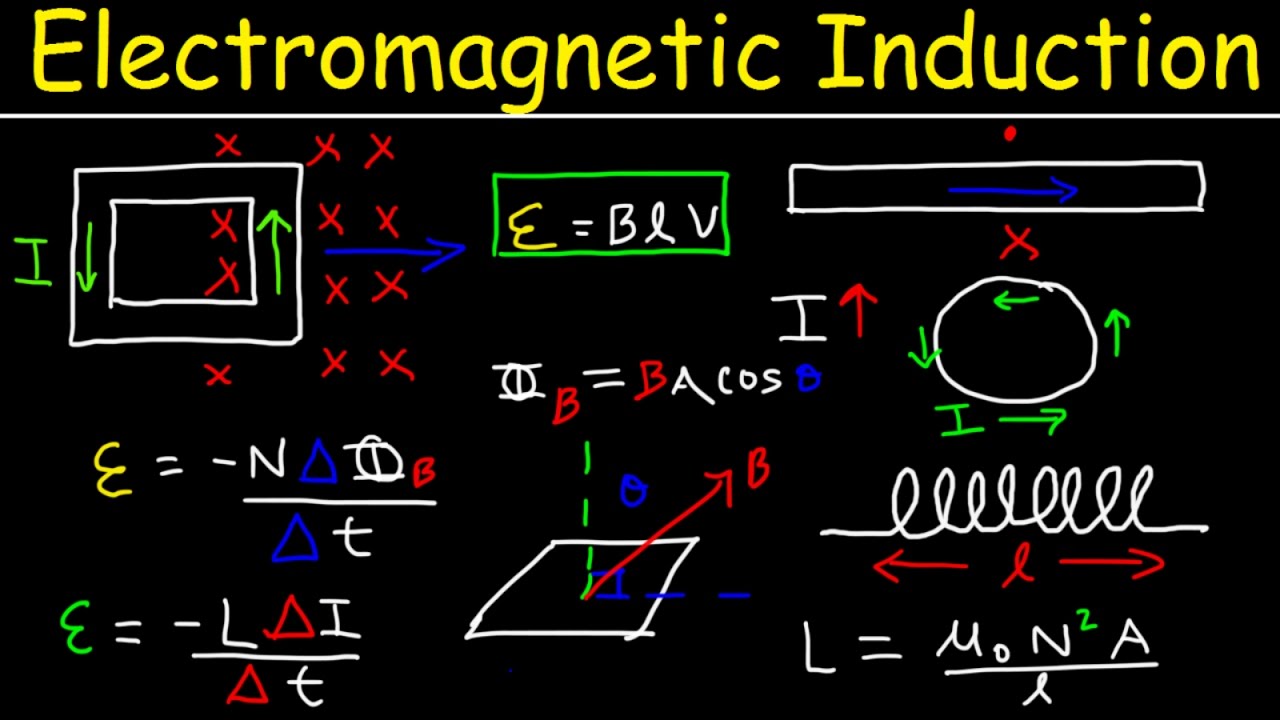
- 📚 The magnetic flux can be calculated using the formula: flux = N * B * A * cos(theta), where N is the number of turns, B is the magnetic field strength, A is the area of the coil, and theta is the angle between the magnetic field and the area vector.
- 📉 The flux changes with time as the angle (theta) between the coil and the magnetic field changes, which is directly related to the rotational motion of the coil.
- 📶 The maximum flux occurs when the angle between the coil and the magnetic field is 0 degrees, resulting in the maximum value of cos(theta).
- 🔄 At a 90-degree angle, the flux is zero because cos(90) = 0, indicating no contribution to the flux from the angle component.
- 🔽 At 180 degrees, the flux is negative, which can be thought of as the coil being oriented in the opposite direction to the magnetic field, resulting in a negative contribution to the flux.
- 📊 The graph of flux over time is a cosine wave, reflecting the periodic nature of the coil's rotation and the changing angle.
- 🔌 The induced electromotive force (emf) is given by the equation: emf = -N * B * A * omega * sin(omega * t), where omega is the angular speed of rotation.
- ⚡ The induced emf is highest when the rate of change of flux is greatest, which occurs at points where the sine function has its maximum or minimum values.
- 🔁 The emf alternates between positive and negative values, creating an alternating current, with the frequency of alternation depending on the rotational speed of the coil.
Q & A
What is the phenomenon described in the video script?
-The script describes the phenomenon of electromagnetic induction, where a voltage is generated in a coil when it is spun inside a magnetic field.
What is the purpose of the video?
-The purpose of the video is to explain how the induced voltage changes over time and to derive an equation that represents this relationship.
What is Faraday's Law mentioned in the script?
-Faraday's Law states that an electromotive force (emf) is induced in a coil when there is a change in the magnetic flux through the coil.
How is the magnetic flux changing as the coil spins?
-The magnetic flux changes due to the changing angle between the magnetic field and the area vector of the coil, which is affected by the spinning motion.
What is the formula for calculating magnetic flux in the context of the video?
-The formula for calculating magnetic flux in this context is Φ = N * B * A * cos(θ), where N is the number of turns, B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the area vector.
What does the angle θ represent in the formula for magnetic flux?
-The angle θ represents the angle between the magnetic field vector and the area vector of the coil.
How does the video script connect the angle θ with time t?
-The script connects the angle θ with time t by using the concept of angular motion, where the angle turned (θ) equals angular speed (ω) times time (t).
What is the equation for the induced emf according to Faraday's Law?
-The equation for the induced emf according to Faraday's Law is emf = -N * B * A * ω * sin(ωt), where N is the number of turns, B is the magnetic field strength, A is the area of the coil, ω is the angular speed, and t is time.
Why is the induced emf zero when the magnetic flux is at its maximum?
-The induced emf is zero when the magnetic flux is at its maximum because at that point, the rate of change of flux (the slope) is zero, as per Faraday's Law, which is concerned with the change in flux, not the flux itself.
What does the negative sign in the equation for induced emf represent?
-The negative sign in the equation for induced emf represents the direction of the induced emf, which is opposite to the direction of the change in magnetic flux, as per Lenz's Law.
How does the frequency of the alternating voltage relate to the spinning of the coil?
-The frequency of the alternating voltage is directly related to the spinning speed of the coil. If the coil spins faster, the frequency of the alternating voltage increases, and vice versa.
What does the term 'emf' stand for in the context of the video script?
-In the context of the video script, 'emf' stands for electromotive force, which is the voltage generated due to the change in magnetic flux through the coil.
Why does the induced emf change between positive and negative values?
-The induced emf changes between positive and negative values because of the sine function in the equation, which represents the alternating nature of the voltage as the coil spins through different angles.
What is the significance of the maximum induced emf (e_naught) in the equation?
-The maximum induced emf (e_naught) represents the peak value of the alternating voltage that can be generated by the spinning coil in the magnetic field.
Outlines
🔌 Understanding Induced Voltage in a Magnetic Field
This paragraph introduces the concept of induced voltage in a coil when it spins inside a magnetic field. It explains that the voltage is generated due to a change in magnetic flux, as per Faraday's law. The video aims to build an equation to describe this voltage and how it changes over time by plotting graphs. The process starts with understanding how the magnetic flux changes, which is crucial for deriving the voltage equation. The magnetic flux is calculated using the formula involving the number of coil turns (n), the magnetic field strength (B), the area of the coil (A), and the cosine of the angle (theta) between the magnetic field and the area vector. The angle changes as the coil spins, affecting the flux and thus the induced voltage.
🌀 Graphing Flux and Induced EMF Over Time
The paragraph delves into the process of graphing the magnetic flux and the induced electromotive force (EMF) as a function of time. It begins by discussing the concept of flux and its relationship with the orientation of the coil in the magnetic field. The flux is shown to be a cosine function of time, with the maximum flux occurring when the coil is parallel to the magnetic field. The induced EMF is then derived from Faraday's law, which states that the induced EMF is equal to the negative rate of change of magnetic flux with respect to time. The differentiation of the flux equation yields an expression for the induced EMF, which depends on the number of turns, the magnetic field strength, the area of the coil, and the angular velocity of the coil. The graph of the induced EMF is predicted to be a sine wave, oscillating between positive and negative maximum values, indicating an alternating voltage. The frequency of this oscillation is related to the rotational speed of the coil.
🔄 The Paradox of Maximum Flux and EMF
This paragraph addresses the counterintuitive relationship between magnetic flux and induced EMF. It explains that while one might expect the induced EMF to be highest when the flux is maximum, Faraday's law focuses on the rate of change of flux. At the points where the flux is maximum or minimum, the rate of change of flux is zero, resulting in zero induced EMF. Conversely, when the flux is changing rapidly, such as when the coil is perpendicular to the magnetic field, the induced EMF is at its maximum. The analogy of standing on a mountain is used to illustrate this concept, where the steepness of the slope (rate of change of flux) determines the induced EMF, not the height of the mountain (flux) itself. This understanding clarifies why the induced EMF is zero at points of maximum flux and maximum when the flux is changing most rapidly.
Mindmap
Keywords
💡Induced Voltage
💡Magnetic Flux
💡Faraday's Law
💡EMF (Electromotive Force)
💡Angular Speed
💡Cosine Function
💡Sine Function
💡Chain Rule
💡Frequency
💡Alternating Voltage
💡Graph
Highlights
The video explores the relationship between voltage and the position of a coil in a magnetic field.
Faraday's law is used to explain the generation of voltage due to a change in magnetic flux through the coil.
The concept of magnetic flux is introduced, which is the product of the field strength, coil area, and the cosine of the angle between them.
The importance of correctly identifying the angle theta between the magnetic field and the area vector is emphasized.
The flux changes with time as the coil rotates, inducing an electromotive force (EMF).
The video encourages viewers to derive the equation for flux as a function of time themselves.
The relationship between angular speed and time is used to express the angle as a function of time.
The maximum flux is identified as the product of the coil's area, the magnetic field strength, and the number of coil turns.
The flux is shown to be zero when the coil is perpendicular to the magnetic field, and negative when it is at 180 degrees.
The concept of negative flux is explained as the change in the direction of the effective 'wind' through the coil.
A cosine function is used to model the flux as a function of time, resulting in a wave-like graph.
Faraday's law is applied to derive the equation for the induced EMF, which is proportional to the rate of change of flux.
The induced EMF is shown to be maximum when the rate of change of the angle is highest, not necessarily when the flux is maximum or minimum.
The video explains the counter-intuitive result that zero EMF is induced when the flux is at its maximum or minimum, due to the rate of change being zero at those points.
The frequency of the induced EMF is related to the rotational speed of the coil, with a higher spin rate leading to a higher frequency.
The video concludes by emphasizing the importance of the rate of change of flux, rather than the flux itself, in inducing EMF.
Transcripts
Browse More Related Video

michael faraday | law of electromagnetic induction | faraday's law of induction

Faraday's Law of Electromagnetic Induction, Magnetic Flux & Induced EMF - Physics & Electromagnetism

EMF and flux explained
Faraday's & Lenz's Law of Electromagnetic Induction, Induced EMF, Magnetic Flux, Transformers

Faradays Law in 3 minutes

Magnetic Induction
5.0 / 5 (0 votes)
Thanks for rating: