11.3 Colligative Properties | High School Chemistry
TLDRThis chemistry lesson delves into colligative properties, which are solution properties that change proportionally with the addition of solute. The instructor explains how these properties, such as freezing point depression, boiling point elevation, and vapor pressure depression, are influenced by the number of particles a solute dissociates into, known as the van 't Hoff factor. The lesson covers the qualitative aspects and quantitative calculations of these properties, using examples like NaCl, methanol, barium hydroxide, and aluminum nitrate to illustrate the concepts. The importance of understanding electrolytes and non-electrolytes in determining the van 't Hoff factor is emphasized, concluding with the application of osmotic pressure in reverse osmosis systems.
Takeaways
- 🧪 Colligative properties are properties of a solution that change proportionally as more solute is added, regardless of the solute's identity.
- 🧊 Freezing points decrease as more solute is added to a solution, disrupting the regular crystalline structure of the solvent.
- 🌡 Boiling points increase with the addition of solute, due to a complex relationship involving entropy rather than just intermolecular forces.
- 🌬 Vapor pressure above a solution decreases as more solute is added, leading to less water vapor in the air, which is related to humidity.
- 🌐 The van 't Hoff factor (i) is crucial in calculating colligative properties, accounting for the number of particles an electrolyte dissociates into.
- 🛠️ Electrolytes are substances that dissociate into ions in solution, affecting the total concentration of particles and thus colligative properties.
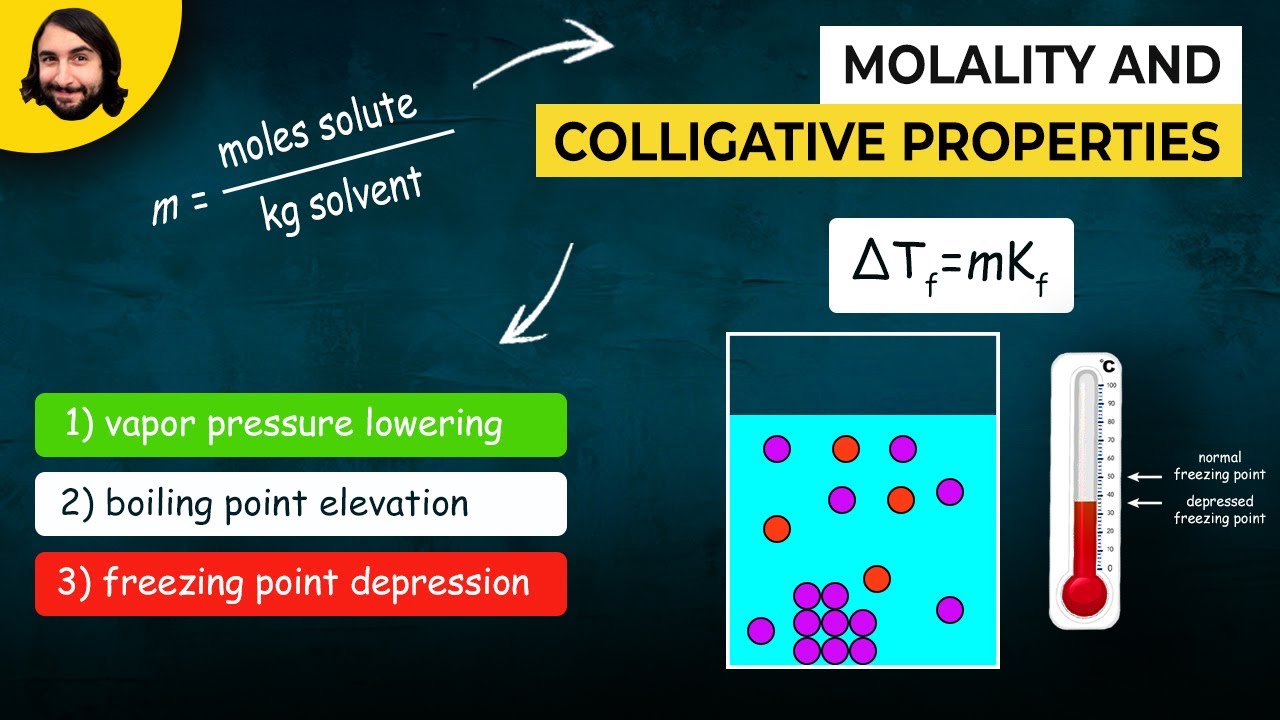
- 🧊🔥 Freezing point depression and boiling point elevation are calculated using the van 't Hoff factor, the molality of the solution, and specific constants for the solvent.
- 💧 Osmotic pressure is the pressure needed to prevent the movement of water across a semi-permeable membrane from a region of low solute concentration to a region of high solute concentration.
- 🌡️ Raoult's law governs vapor pressure depression, relating the partial pressure of a solvent in a solution to its mole fraction and the vapor pressure of the pure solvent.
- 🚰 Reverse osmosis systems utilize high pressure to force water through a semi-permeable membrane, purifying it by overcoming osmotic pressure.
Q & A
What are colligative properties?
-Colligative properties are properties of a solution that change proportionally as you add solute. They include freezing point depression, boiling point elevation, vapor pressure depression, and osmotic pressure. The identity of the solute doesn't matter as much as the amount added.
How do colligative properties relate to the identity of the solute?
-The identity of the solute is not as important as the amount added. Colligative properties change as more solute is added, regardless of the solute's identity, because the presence of any solute disrupts the solvent's structure.
What is the role of the van 't Hoff factor in colligative properties?
-The van 't Hoff factor (represented by the symbol i) accounts for the number of particles an electrolyte dissociates into. It is crucial in calculating the total concentration of particles in a solution, which affects colligative properties.
How does the addition of solute affect the freezing point of a solution?
-As more solute is added to a solution, the freezing point decreases. This is known as freezing point depression and is used in practices like salting roads to prevent ice formation.
What is the relationship between solute addition and boiling point in a solution?
-Unlike freezing points, boiling points increase as more solute is added to a solution. This phenomenon is known as boiling point elevation.
Why does vapor pressure decrease when a solute is added to a liquid?
-Vapor pressure decreases because the added solute molecules disrupt the liquid's surface, reducing the number of solvent molecules that can escape into the vapor phase. This is described by Raoult's law.
How does osmotic pressure relate to the diffusion of water?
-Osmotic pressure is the pressure that needs to be applied to prevent the net movement of water across a semi-permeable membrane from a region of lower solute concentration to a region of higher solute concentration. It is a measure of the tendency of water to diffuse.
What is the significance of the van 't Hoff factor in calculating osmotic pressure?
-The van 't Hoff factor is important in calculating osmotic pressure because it accounts for the total number of ions produced when an electrolyte dissolves, which affects the molarity and thus the osmotic pressure.
How is the freezing point depression calculated?
-Freezing point depression is calculated using the equation ΔTf = -i * Kf * m, where i is the van 't Hoff factor, Kf is the freezing point constant, and m is the molality of the solution.
What is the practical application of understanding colligative properties?
-Understanding colligative properties has practical applications in various fields such as chemistry, environmental science, and engineering. For example, it helps in understanding the effects of solutes on the physical properties of solutions, which is crucial in processes like desalination and pharmaceutical formulation.
Outlines
🧪 Colligative Properties in Chemistry
This paragraph introduces the concept of colligative properties, which are properties of a solution that change proportionally with the addition of solute. It emphasizes that the identity of the solute is less important than the number of particles it contributes to the solution. The paragraph discusses how solute particles disrupt the intermolecular forces, particularly hydrogen bonding in water, and how this disruption affects properties like freezing points, boiling points, and vapor pressure. The van 't Hoff factor is introduced as a way to account for the number of particles an electrolyte dissociates into, which is crucial for understanding how colligative properties are affected by different solutes.
🌡️ Understanding Freezing Point Depression
The second paragraph delves into the colligative property of freezing point depression, explaining how the addition of solute to a solvent lowers the freezing point. It uses the example of salting roads in cold climates to illustrate how this principle is applied in real life. The explanation includes the concept of a regular crystalline structure of ice and how the presence of solute disrupts this structure, requiring a lower temperature for the solution to freeze. The paragraph also mentions the importance of the van 't Hoff factor in determining the extent of freezing point depression.
🔍 Exploring Boiling Point Elevation and Vapor Pressure Depression
This paragraph discusses two additional colligative properties: boiling point elevation and vapor pressure depression. It explains that, unlike freezing points, boiling points increase with the addition of solute, and the vapor pressure above a solution decreases. The explanation touches on the concepts of entropy and Raoult's law, which governs vapor pressure depression. The paragraph also poses hypothetical questions to illustrate how these properties are affected by different concentrations and types of solutes, emphasizing the importance of understanding the van 't Hoff factor in predicting the behavior of solutions.
📚 The Mathematics of Colligative Properties
The fourth paragraph introduces the mathematical equations used to calculate the changes in freezing and boiling points due to the presence of solutes. It provides the formulas for freezing point depression and boiling point elevation, including the roles of the van 't Hoff factor, molality, and specific constants for water. The paragraph also clarifies potential confusion regarding the presence or absence of a negative sign in these equations, explaining that a negative change indicates a decrease in temperature, as seen with freezing points.
🌡️ Calculating Vapor Pressure and Osmotic Pressure
This paragraph continues the mathematical theme by discussing Raoult's law, which relates to vapor pressure depression, and introduces the concept of osmotic pressure. It explains how to calculate the vapor pressure above a solution using mole fractions and provides an example calculation for an aqueous solution of methanol. The paragraph also outlines the equation for osmotic pressure and sets the stage for a discussion on osmosis and diffusion, which are key to understanding how osmotic pressure is generated.
💧 Osmosis and Osmotic Pressure in Action
The final paragraph explores the concept of osmosis, the diffusion of water from an area of high concentration to an area of low concentration, and how it relates to osmotic pressure. It describes an experiment involving a semi-permeable membrane separating pure water from a salt solution, resulting in a pressure difference that can be calculated using the provided equation. The paragraph also explains the practical application of osmotic pressure in reverse osmosis systems, which use pressure to purify water by forcing it through a membrane that solutes cannot cross, leading to an increase in solute concentration and a rise in osmotic pressure.
Mindmap
Keywords
💡Colligative Properties
💡Freezing Point Depression
💡Boiling Point Elevation
💡Vapor Pressure Depression
💡Osmotic Pressure
💡Van 't Hoff Factor
💡Electrolytes
💡Non-Electrolytes
💡Molality
💡Raoult's Law
💡Osmosis
Highlights
Colligative properties are properties of a solution that change proportionally as solute is added.
The identity of the solute does not matter for colligative properties, only the amount added affects the changes.
Freezing points decrease and boiling points increase as more solute is added to a solution.
Vapor pressure above a solution decreases as more solute is added.
Electrolytes that dissociate into multiple ions affect colligative properties differently, factored in by the van 't Hoff factor.
The van 't Hoff factor (i) represents the total ions an electrolyte dissociates into.
Non-electrolytes have a van 't Hoff factor of one, as they do not dissociate into additional particles.
Four fundamental colligative properties are freezing point depression, boiling point elevation, vapor pressure depression, and osmotic pressure.
Salting roads in cold climates lowers the freezing point of water, preventing ice formation.
Freezing point depression is due to the disruption of the crystalline structure of ice by solute molecules.
Boiling point elevation is related to entropy, not just intermolecular forces.
Vapor pressure depression is governed by Raoult's law, which relates the partial pressure of a solvent to its mole fraction in a solution.
Osmotic pressure is the force needed to prevent the movement of water across a semi-permeable membrane due to differences in solute concentration.
The van 't Hoff factor is crucial in calculating the total solute concentration in solutions, affecting colligative properties.
In solutions with different concentrations, the total concentration of dissolved species (considering the van 't Hoff factor) determines the extent of colligative property changes.
Osmotic pressure can be calculated using the equation π = iMRT, where π is osmotic pressure, i is the van 't Hoff factor, M is molarity, R is the gas constant, and T is temperature in Kelvin.
Reverse osmosis systems work by applying pressure greater than the osmotic pressure to purify water.
Transcripts
Browse More Related Video

13.3 Colligative Properties | General Chemistry

Colligative Properties - Boiling Point Elevation, Freezing Point Depression & Osmotic Pressure
Molality and Colligative Properties

Lec-05 I Colligative properties I Applied Chemistry I Chemical Engineering

Molarity , Molality or Mole Fraction || 3D animated explanation || solutions || class12thchemistry

Boiling point elevation and freezing point depression | Chemistry | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: