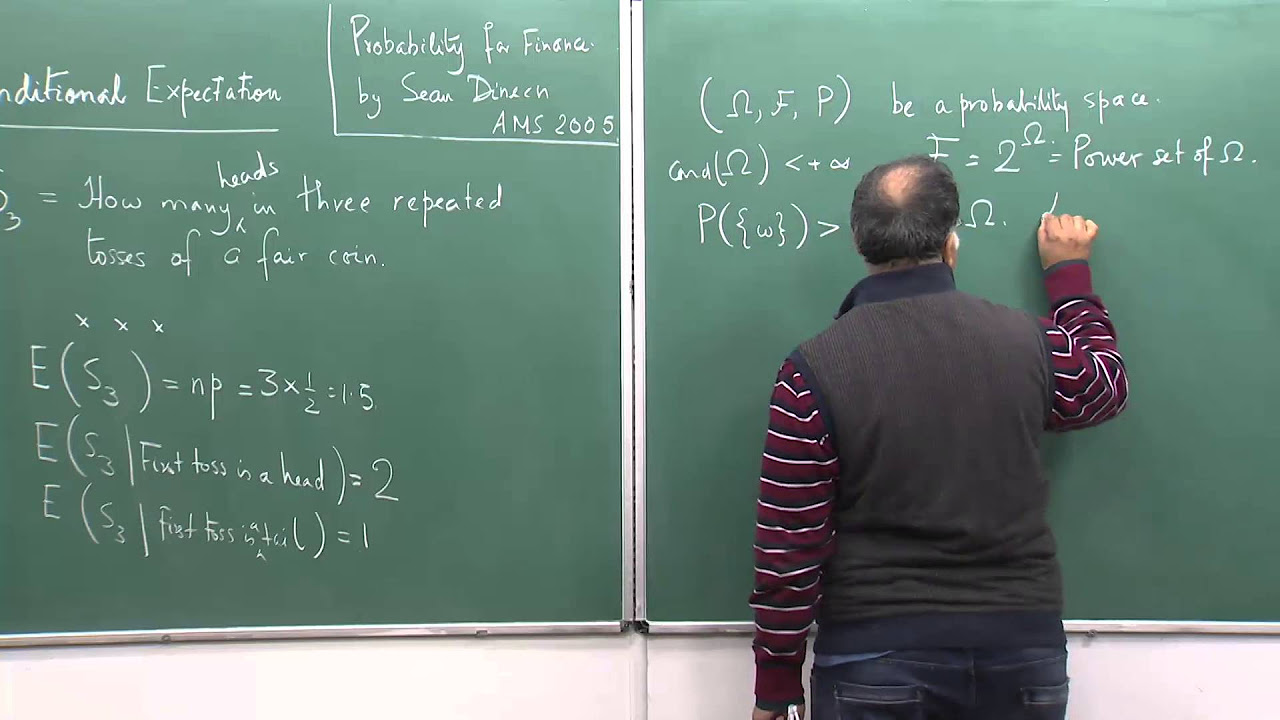Conditional Expextation-II
TLDRThe lecture delves into the concept of conditional expectation in probability theory, particularly when the Sigma-algebra G isn't given by a countable partition. It discusses the generalization of conditional expectation, the Radon-Nikodym theorem, and the existence of a measurable random variable that represents this expectation. The instructor outlines key properties of conditional expectation pivotal for finance and Martingales, emphasizing the importance of understanding these concepts for derivative pricing and stock market behavior.
Takeaways
- 📚 The concept of conditional expectation is discussed in the context of a sigma-algebra G that is not necessarily a countable partition of omega.
- 🧩 The existence of a G-measurable random variable E(X|G) is not immediately provable and requires deeper probability theory to establish.
- 📉 The conditional expectation is defined as a G-measurable random variable that integrates to the same value as X over any set A in G, a property sometimes called partial averaging.
- 💡 The existence of such a conditional expectation hinges on the construction of a new probability measure from an existing one, a key concept in finance and probability theory.
- 📌 The Radon-Nikodym theorem is introduced as a fundamental result that allows for the construction of a new probability measure Q from an existing measure P, given certain conditions.
- 🔍 The theorem ensures the existence of a nonnegative, integrable random variable Y, known as the Radon-Nikodym derivative, which is essential for representing measure Q in terms of measure P.
- 🎯 The uniqueness of the conditional expectation is highlighted, noting that while the random variable may not be unique, it exhibits the desired partial averaging property almost everywhere.
- 🔄 The properties of conditional expectation are outlined, including the 'taking out what is known' property, the property of nested expectations, and the independence property.
- 🏗️ The script emphasizes the importance of understanding these properties for applications in finance, particularly in the study of Martingales and derivative pricing.
- 🎲 A connection is drawn between the stock market and gambling, highlighting the importance of understanding the growth of money in the stock market compared to fixed deposits or government bonds.
- 📝 The script concludes with an encouragement to engage with the material deeply, including doing exercises and utilizing various resources to solidify understanding.
Q & A
What is conditional expectation and why is it significant in probability theory and finance?
-Conditional expectation is a random variable that represents the expected value of another random variable given some information represented by a Sigma-algebra. It is significant in probability theory and finance because it allows for the prediction of future outcomes based on current information, which is fundamental in risk assessment and decision-making processes in finance.
How is conditional expectation defined when the Sigma-algebra G is not given by a countable partition?
-When the Sigma-algebra G is not given by a countable partition, conditional expectation is defined as a G-measurable random variable that satisfies the property of 'partial averaging', meaning that the integral of this variable over any set A in G is equal to the integral of the original random variable X over the same set A.
What is the concept of 'partial averaging' in the context of conditional expectation?
-'Partial averaging' refers to the property where the integral of the conditional expectation of a random variable X over a set A, given a Sigma-algebra G, is the same as the integral of X over A. This property is used to define conditional expectation when G is not a countable partition.
Why is the existence of a G-measurable random variable important for defining conditional expectation?
-The existence of a G-measurable random variable is crucial because it ensures that there is at least one random variable that can represent the conditional expectation. Without such a random variable, the concept of conditional expectation would not be well-defined.
What is the Radon-Nikodym theorem, and how does it relate to the existence of conditional expectation?
-The Radon-Nikodym theorem is a result in measure theory that states if a measure Q is absolutely continuous with respect to another measure P, then there exists a non-negative, integrable random variable Y (called the Radon-Nikodym derivative) such that Q(A) can be represented as the integral of Y with respect to P over A. This theorem is related to the existence of conditional expectation because it provides a mathematical framework for constructing new probability measures, which is a step in proving the existence of a conditional expectation.
How does the Radon-Nikodym theorem help in constructing a new probability measure from an old one?
-The Radon-Nikodym theorem provides a method to construct a new probability measure Q from an existing one P by using a non-negative, integrable random variable Y as the Radon-Nikodym derivative. This new measure Q is defined such that for any event A, Q(A) is the integral of Y with respect to P over A.
What is the 'taking out what is known' property of conditional expectation?
-The 'taking out what is known' property states that if X is a random variable that is measurable with respect to a Sigma-algebra G (meaning G contains all information about X), then the conditional expectation of X given G is simply X itself, because all information about X is already known within G.
What does it mean for two random variables to be independent with respect to a Sigma-algebra?
-Two random variables X and Y are said to be independent with respect to a Sigma-algebra G if the occurrence of any event A in G does not affect the probability distribution of X. In other words, the value of X does not depend on the information contained in G.
What is the tower property of conditional expectation, and how is it used in finance?
-The tower property of conditional expectation states that the conditional expectation of a random variable X given a Sigma-algebra G, conditioned further on another Sigma-algebra H contained in G, is the same as the conditional expectation of X given H alone. This property is used in finance to make sequential predictions based on nested information sets.
How are the properties of conditional expectation used in the study of Martingales and derivative pricing?
-The properties of conditional expectation are pivotal in understanding Martingales, which are sequences of random variables for which the expected value of the next term in the sequence given all previous terms is the current term. In derivative pricing, these properties help in assessing the expected payoff of financial derivatives based on current information, which is essential for determining their fair value.
Outlines
📚 Generalizing Conditional Expectation
The paragraph discusses the concept of conditional expectation beyond the context of a countable partition of the sample space, omega. It explains that while a countable partition allows for a straightforward proof of conditional expectation, the general case with any sigma-algebra requires deeper probability theory. The speaker introduces the idea of constructing a new probability measure from an existing one, suggesting that this is key to understanding conditional expectation in a more general setting. The paragraph also hints at the Radon-Nikodym theorem, which is central to this discussion but is not fully explored due to the complexity of the topic.
🧩 Constructing New Probability Measures
This paragraph delves into the process of constructing a new probability measure from an existing one, using a non-negative integrable random variable X that equals 1. The function Q is introduced as a way to map elements of a sigma-algebra to real numbers, which leads to the creation of a new probability measure. The paragraph also touches on the concept of absolute continuity between two probability measures, P and Q, and how it relates to the zeros of P implying the zeros of Q. The importance of this process in finance and probability theory is emphasized.
📉 The Radon-Nikodym Theorem
The Radon-Nikodym theorem is the focus of this paragraph, which states that if P(A) = 0 implies Q(A) = 0 for events A in a sigma-algebra, then there exists a non-negative, integrable random variable Y, known as the Radon-Nikodym derivative, that allows for the construction of Q from P. The theorem is highlighted as a deep result in measure theory and probability, emphasizing the importance of proving the existence of such a variable, even though it may not be unique.
🎯 Existence of Conditional Expectation
The paragraph presents the result that for an integrable random variable X on a probability space with a sub-sigma field G, there exists a random variable E(X|G) that satisfies the partial averaging property. It is noted that while this random variable may not be unique, its existence is guaranteed, which is crucial for understanding conditional expectation in a general setup. The paragraph also discusses the implications of finding another random variable Y that satisfies the same property, suggesting that Y must be the conditional expectation of X given G.
📝 Properties of Conditional Expectation
This paragraph outlines the properties of conditional expectation that are essential for understanding and applying the concept in finance. The first property, 'taking out what is known,' allows for the simplification of expressions involving known random variables and their conditional expectations. The second property is the expectation of a conditional expectation, which simplifies to the original expectation. The paragraph promises further exploration of these properties through exercises and homework, indicating their foundational role in the study of finance and related topics.
🔗 Independence and the Tower Property
The concept of independence between a random variable X and a sigma-algebra G is introduced, explaining that if X is independent of G, the conditional expectation of X given G is a constant. The paragraph also introduces the 'tower property' of conditional expectation, which describes how the conditional expectation of X given G can be further conditioned on a sub-sigma field H, effectively simplifying to E(X|H). The importance of these properties in the study of finance and Martingales is emphasized, with a teaser for the upcoming discussion on these topics.
🚀 Conclusion and Future Outlook
In the concluding paragraph, the speaker emphasizes the importance of understanding the properties of conditional expectation, especially in the context of finance and derivative pricing. The speaker encourages students to engage with the material through exercises and to utilize various resources for learning. There is a nod to the practical applications of these concepts in the stock market and an anticipation of future lessons on Martingales and geometric Brownian motion, which are foundational for understanding financial markets.
Mindmap
Keywords
💡Conditional Expectation
💡Sigma-Algebra
💡G-Measurable Random Variable
💡Countable Partition
💡Radon-Nikodym Theorem
💡Probability Measure
💡Absolutely Continuous
💡Indicator Function
💡Independence
💡Tower Property
💡Martingales
Highlights
Introduction to the concept of conditional expectation without a given Sigma-algebra G by a countable partition.
Explanation of the conditional expectation as a G measurable random variable that integrates to the same value as the original random variable X over any set A in G.
Discussion on the non-uniqueness of the conditional expectation and the conditions under which it exists.
The importance of constructing a new probability measure from an old one in finance and probability theory.
Process of creating a new probability measure Q from an existing probability measure P using a non-negative integrable random variable X.
The Radon-Nikodym theorem
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: