Deriving the Range Equation of Projectile Motion

Flipping Physics
16 Jun 201407:31
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging educational transcript, a group of students and their teacher delve into the derivation of the projectile motion range equation. The discussion involves breaking down the initial velocity into components, understanding constant velocity in the x-direction, and using uniformly accelerated motion equations in the y-direction. The session culminates in the derivation of the range equation, highlighting the importance of understanding the fundamental concepts of projectile motion, such as initial velocity, launch angle, and the acceleration due to gravity.

Takeaways
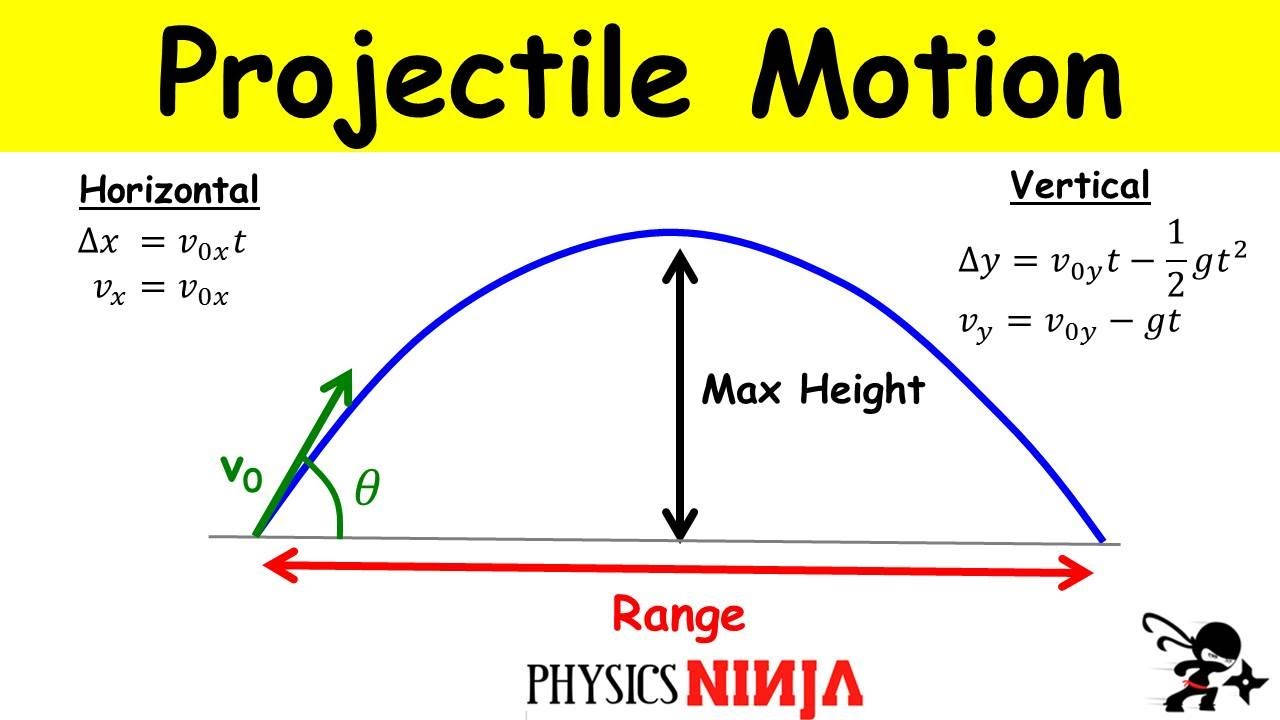
  • 📌 The range of a projectile is the displacement in the x-direction when the displacement in the y-direction is zero.
  • 📐 The range equation is derived from the initial velocity's components and the acceleration due to gravity (g).
  • 🚀 The initial velocity is not broken into components when using the range equation, but it is necessary for its derivation.
  • 🔄 The sine of the launch angle (theta) relates the initial velocity in the y-direction to the initial velocity itself.
  • 🔄 The cosine of the launch angle (theta) relates the initial velocity in the x-direction to the initial velocity itself.
  • 🕒 The displacement in the x-direction (range) is calculated by multiplying the x-component of the initial velocity by the change in time.
  • 📉 In the y-direction, the displacement is zero, and the acceleration is the negative acceleration due to gravity (-g).
  • 🔢 The change in time is found using the uniformly accelerated motion equation for the y-direction, with the initial velocity in the y-direction being negative 1/2 g times the change in time.
  • 🔄 The Double Angle Formula is not required to use the range equation, but it is used in the final step of its derivation.
  • 📈 The derived range equation is the magnitude of the initial velocity squared, times the sine of two times the launch angle, all divided by the acceleration due to gravity (g).
  • 📚 The range equation is a fundamental concept in projectile motion, encapsulating the effects of initial velocity, launch angle, and gravity on the horizontal displacement of a projectile.
Q & A

  • What is the definition of the range of a projectile?

    -The range of a projectile is defined as the displacement in the x-direction when the displacement in the y-direction equals zero.

  • What is the general form of the range equation?

    -The general form of the range equation is Range = (initial velocity)^2 * sin(2 * launch angle) / acceleration due to gravity (g).

  • Why do we not need to break the initial velocity into its components when using the range equation?

    -We do not need to break the initial velocity into its components when using the range equation because the equation itself already accounts for the components through the sine and cosine of the launch angle.

  • How are the components of the initial velocity in the x and y directions related to the initial angle and velocity magnitude?

    -The initial velocity in the y-direction is given by (initial velocity) * sin(initial angle), and the initial velocity in the x-direction is given by (initial velocity) * cos(initial angle).

  • What is the significance of the acceleration due to gravity (g) in the range equation?

    -The acceleration due to gravity (g) is a positive constant that affects the vertical motion of the projectile. It is used in the range equation to determine the time of flight and, consequently, the horizontal range.

  • How does the uniformly accelerated motion equation help in deriving the range equation?

    -The uniformly accelerated motion equation is used to relate the displacement in the y-direction to the initial velocity in the y-direction, the change in time, and the acceleration due to gravity. This relationship is crucial for finding the time of flight, which is then used in the range equation.

  • What is the relationship between the change in time and the initial velocity components in the y-direction?

    -The change in time can be found by the equation: (change in time) = 2 * (initial velocity in the y-direction) / g. This relationship is derived from the uniformly accelerated motion equation with the displacement in the y-direction being zero.

  • Why is the displacement in the y-direction considered to be zero in the context of deriving the range equation?

    -The displacement in the y-direction is considered zero because the range is defined at the point where the projectile returns to its initial height, which is the point of maximum horizontal displacement.

  • What is the Double Angle Formula mentioned in the script, and how does it relate to the range equation?

    -The Double Angle Formula states that 2 * sin(theta) * cos(theta) = sin(2 * theta). This formula is used in the final step of deriving the range equation to simplify the expression involving the sine and cosine of the launch angle.

  • How does the final derived range equation look?

    -The final derived range equation is Range = (initial velocity)^2 * sin(2 * launch angle) / g.

  • What are the key variables in the range equation, and what do they represent?

    -The key variables in the range equation are: (initial velocity)^2, which is the square of the magnitude of the initial velocity; sin(2 * launch angle), which represents the sine of twice the launch angle; and g, which is the positive acceleration due to gravity.

Outlines
00:00
📚 Introduction to Projectile Motion and Range Equation

This paragraph introduces the topic of projectile motion, specifically focusing on deriving the range equation. Mr. P explains that the range is the displacement in the x-direction when the displacement in the y-direction is zero. The range equation is presented as the initial velocity squared, times the sine of two times the launch angle, divided by the acceleration due to gravity. The students, Billy, Bo, and Bobby, engage in a discussion about the components of the initial velocity and how they relate to the range equation. Mr. P emphasizes the importance of using variables rather than numbers when deriving the equation. Bo lists the known quantities in the x and y directions, and Bobby begins to solve for displacement in the x-direction, leading to an equation for range in terms of change in time, initial velocity, and launch angle.

05:01
🧠 Deriving the Range Equation and Understanding its Components

In this paragraph, the class continues the derivation of the range equation by focusing on the y-direction and solving for the change in time. Billy uses the uniformly accelerated motion equation to find the change in time, relating it to the initial velocity in the y-direction and the acceleration due to gravity. The class then substitutes the expression for change in time back into the range equation, leading to a rearrangement of terms. Mr. P clarifies that the double angle formula is not required for using the range equation but is essential for the final step in deriving it. The paragraph concludes with the complete derivation of the range equation, emphasizing the definitions of range, initial velocity, and launch angle, and the positive nature of the acceleration due to gravity. Mr. P thanks the students for their participation and learning.

Mindmap
Keywords
💡Projectile Motion
Projectile motion refers to the motion of an object that is launched into the air and moves under the influence of gravity and air resistance. In the context of the video, it is the study of how an object moves when thrown near the Earth's surface, considering only the gravitational force acting upon it. The main theme of the video revolves around deriving the range equation for projectile motion, which is a fundamental concept in physics.
💡Range Equation
The range equation is a mathematical formula used to calculate the maximum horizontal distance (range) that a projectile will travel before landing. It is derived from the equations of motion for an object moving under the influence of gravity. In the video, the range equation is derived through a step-by-step process involving the initial velocity, launch angle, and the acceleration due to gravity.
💡Initial Velocity
Initial velocity is the speed at which an object is moving when it is launched or set into motion. It is a vector quantity, meaning it has both magnitude and direction. In the context of the video, the initial velocity is a critical factor in determining the range of a projectile, as it influences both the horizontal and vertical components of the motion.
💡Launch Angle
The launch angle is the angle between the initial velocity vector and the horizontal direction when a projectile is launched. It plays a significant role in determining the trajectory and range of the projectile. A higher launch angle can result in a greater range, assuming the initial velocity is constant.
💡Acceleration Due to Gravity
Acceleration due to gravity, often denoted as 'g', is the acceleration that an object experiences due to the Earth's gravitational pull. On the Earth's surface, it is approximately 9.81 meters per second squared, always directed downwards. In the video, 'g' is a key factor in the equations used to derive the range equation, representing the constant downward force acting on the projectile.
💡Displacement
Displacement is the change in position of an object, usually represented as a vector quantity with both magnitude and direction. In the context of the video, displacement in the x and y directions is crucial for understanding the projectile's trajectory and calculating its range.
💡Components of Initial Velocity
The components of initial velocity refer to the horizontal (x-direction) and vertical (y-direction) parts of the total initial velocity. These components are essential for analyzing the motion of a projectile in two dimensions. In the video, although the initial velocity is not broken down into components for the range equation, understanding these components is vital for a complete analysis of projectile motion.
💡Sine and Cosine of Launch Angle
The sine and cosine of the launch angle are trigonometric functions that describe the ratio of the opposite side and the adjacent side, respectively, in a right-angled triangle. In the context of projectile motion, they are used to resolve the initial velocity into its horizontal and vertical components, which are then used in the equations for calculating the projectile's trajectory.
💡Uniformly Accelerated Motion
Uniformly accelerated motion refers to the type of motion where an object's acceleration remains constant throughout. In the case of projectile motion, the only acceleration acting on the object (ignoring air resistance) is the constant acceleration due to gravity. The uniformly accelerated motion in the vertical direction is used to derive the time of flight, which is then used to calculate the range.
💡Double Angle Formula
The double angle formula is a trigonometric identity that states that twice the sine of an angle multiplied by the cosine of the same angle is equal to the sine of twice the angle. While not necessary for using the range equation, it is used in the derivation of the equation to simplify the expression involving the sine of two times the launch angle.
💡Change in Time
Change in time, often referred to as the time of flight, is the total duration for which a projectile is in motion from the moment it is launched until it lands. In the context of the video, the change in time is crucial for calculating the displacement in the y-direction and subsequently the range of the projectile.
Highlights

Introduction to projectile motion and the range equation.

Definition of projectile range as displacement in x-direction when y-displacement is zero.

The range equation is derived from the components of initial velocity and acceleration due to gravity.

Initial velocity does not need to be broken into components to use the range equation.

Derivation of the range equation requires breaking the initial velocity into its x and y components.

Explanation of sine and cosine components for the initial velocity in y and x directions respectively.

Deriving the range equation involves using variables, not specific numbers.

Description of projectile motion in the x-direction as constant velocity motion.

Clarification on not using numbers when deriving equations, only variables.

Solving for displacement in x-direction and relating it to the change in time and velocity components.

Derivation of the change in time using the uniformly accelerated motion equation for y-direction.

Substitution of the change in time equation back into the range equation.

Re-arrangement of the range equation to its final form.

Discussion on not requiring knowledge of the Double Angle Formula for using the range equation.

Final form of the range equation incorporating the sine of two times the launch angle.

Confirmation of the acceleration due to gravity being a positive number.

Summary of the range equation and its components, including initial velocity, launch angle, and gravity.

Conclusion of the learning session and acknowledgment of the class's participation.

Transcripts

Browse More Related Video

Projectile Motion: Finding the Maximum Height and the Range

Range Equation Derivation

Understanding the Range Equation of Projectile Motion

Why Does 45º Launch Angle Give Maximum Range? // HSC Physics

Projectile Motion (AP Physics 1)

AP Physics - Projectile Motion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationProjectileMotionRangeEquationInteractiveLessonMathDerivationTeachingMethodClassroomDiscussionLearningProcessPhysicsConceptsEducationalContent