Epsilon-Delta Definition of Functional Limits | Real Analysis

Wrath of Math

20 Jun 202321:38

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the rigorous definition of continuity and the limit of a function, focusing on the Epsilon-Delta definition. It explains the concept of limits without considering the function's value at the limit point, using illustrations and examples to clarify. The script also covers the negation of the definition, showing how to prove a function does not have a certain limit, and provides exercises to practice proving limits using the Epsilon-Delta method, including a walkthrough for a linear function and a quadratic function.

Takeaways

📚 The video discusses the rigorous definition of continuity and the limit of a function, focusing on the Epsilon-Delta definition.
🔍 The limit of a function, f(x) as x approaches a point C, is defined as L, meaning f(x) gets arbitrarily close to L as x gets arbitrarily close to C.
⚠️ The actual value of the function at point C (f(C)) is not relevant to the definition of the limit; only the behavior of f(x) as x approaches C is considered.
📉 The Epsilon-Delta definition states that for every positive Epsilon, there exists a Delta such that if x is within Delta of C, then f(x) is within Epsilon of L.
📈 The video uses visual illustrations to help understand the Epsilon-Delta definition and its implications for the limit of a function.
📝 The negation of the limit definition is also explained, describing what it means for a function to not have a particular limit at a point.
📋 Two Epsilon-Delta proofs are provided to demonstrate how to prove that the limit of a function at a point is a specific value.
🔢 The first proof involves a linear function, f(x) = 4x + 1, and shows that its limit as x approaches 3 is 13.
🧩 The second proof involves proving the limit of f(x) = x^2 as x approaches 2 is 4, which includes handling an additional complexity of the proof.
📚 The importance of scratch work in proofs is emphasized, where one assumes the conclusion and works backward to determine an appropriate Delta.
🎓 The video concludes with a practice exercise for the viewer to apply the Epsilon-Delta definition to prove the limit of a given rational function as x approaches 3 is 24.

Q & A

What is the primary goal of defining the limit of a function in a rigorous manner?
-The primary goal is to capture the concept that as x approaches a certain point C, the function f(x) gets arbitrarily close to a specific value L, without actually needing to evaluate the function at point C.
What is the formal definition of the limit of a function using the Epsilon-Delta approach?
-The limit of a function f(x) as x approaches C is L, if for all Epsilon > 0, there exists some Delta > 0 such that for every x within Delta of C (but x ≠ C), f(x) is within Epsilon of L.
How does the Epsilon-Delta definition relate to the concept of 'neighborhoods'?
-The definition can be restated in terms of neighborhoods, where for every Epsilon neighborhood of L, there exists a corresponding Delta neighborhood of C such that if x is in the Delta neighborhood, then f(x) is in the Epsilon neighborhood of L.
What does it imply if the limit of a function as x approaches C does not exist?
-It implies that there exists some tolerance Epsilon > 0 such that no matter how close x gets to C, there will always be some x within that closeness where f(x) is not within the tolerance Epsilon of any proposed limit value.
Why is it important to note that C does not need to be in the domain of the function when defining the limit?
-It is important because the limit is concerned with the behavior of the function as x approaches C, not the value of the function at C. C needs to be a limit point of the domain so that x can approach C, but the actual value of f(C) is irrelevant.
What is the negation of the Epsilon-Delta definition, and what does it imply?
-The negation states that there exists some Epsilon > 0 such that for every Delta > 0, there is at least one x within Delta of C where f(x) is not within Epsilon of the proposed limit L. It implies that the function does not converge to L as x approaches C.
How does one typically approach proving that the limit of a function is a particular value using the Epsilon-Delta definition?
-One starts by assuming the function is close to the limit L within a given Epsilon, then performs scratch work to find an appropriate Delta that ensures this closeness. The proof involves setting Delta to a specific value and showing that for all x within Delta of C, f(x) is within Epsilon of L.
What is the significance of the minimum function when choosing Delta in an Epsilon-Delta proof?
-The minimum function is used to satisfy multiple conditions on Delta simultaneously. By setting Delta to the minimum of these conditions, it ensures that all necessary restrictions are met for the proof to hold.
Can you provide an example of a function and its limit that was discussed in the script?
-One example given is the function f(x) = 4x + 1. It was proven that the limit of this function as x approaches 3 is 13 using the Epsilon-Delta definition.
What is the final exercise proposed in the script for the viewer to try on their own?
-The final exercise is to prove that the limit of the function f(x) = (x^2 - 9) / (x - 3) as x approaches 3 is 24, using the Epsilon-Delta definition.

Outlines

00:00

📚 Introduction to the Epsilon Delta Definition of Limits

This paragraph introduces the concept of limits in calculus, emphasizing the need for a rigorous definition. It explains that the limit of a function as x approaches a certain point C is defined without considering the value of the function at C itself. The Epsilon Delta definition is highlighted as the formal approach to defining limits, where for any given tolerance level (Epsilon), there exists a corresponding 'closeness' level (Delta) to the point C that ensures the function's value stays within the Epsilon neighborhood of the limit L. The paragraph also includes an illustration to help visualize this definition.

05:02

🔍 Exploring the Epsilon Delta Definition and Its Negation

This paragraph delves deeper into the Epsilon Delta definition, discussing its implications and providing a visual representation. It clarifies that the point C, where x approaches, does not need to be within the domain of the function, as long as it is a limit point. The paragraph also explains the negation of the definition, which states the conditions under which a function does not have a particular limit. This involves showing that no matter how close x gets to C, the function's value cannot stay within an Epsilon neighborhood of a proposed limit L. The negation is illustrated with a diagram to demonstrate the concept.

10:04

📘 Applying the Epsilon Delta Definition in Proofs

The paragraph focuses on applying the Epsilon Delta definition to prove the limit of a function at a specific point. It provides a step-by-step guide on how to perform scratch work to find an appropriate Delta value that ensures the function's value stays within an Epsilon neighborhood of the limit. The process involves assuming the function is close to the limit and then solving for the conditions under which this assumption holds. The paragraph includes an example with a linear function to demonstrate the proof process.

15:06

📘 Advanced Epsilon Delta Proofs with Quadratic Functions

Building on the previous paragraph, this section tackles a more complex example involving a quadratic function. It outlines the scratch work process for setting up an Epsilon Delta proof, which includes factoring and manipulating inequalities to find a suitable Delta. The paragraph explains the need to consider upper bounds for certain expressions and how to combine these with the Epsilon Delta definition to prove that the limit of the function as x approaches a specific value is another specific value.

20:07

📝 Practice Exercise and Encouragement for Understanding Limits

The final paragraph presents a practice exercise for the viewer, challenging them to apply the Epsilon Delta definition to prove the limit of a given rational function as x approaches a certain value. It encourages viewers to undertake scratch work to determine the appropriate Delta and then to construct a proof. The paragraph concludes with an invitation to check the video description for additional resources and support for the Wrath of Math on Patreon.

Mindmap

Keywords

💡Continuity

Continuity in mathematics, particularly in calculus, refers to the property of a function that guarantees the output of the function gets arbitrarily close to a certain value as the input gets arbitrarily close to a specific point. In the video, continuity is discussed as a concept that needs a rigorous definition, which is foundational to understanding the limit of a function. The script mentions that the formal definition of continuity will rely on the definition of the limit of a function.

💡Limit of a Function

The limit of a function is a fundamental concept in calculus that describes the behavior of a function as its input approaches a certain value. The script delves into the formal definition of the limit using the Epsilon-Delta definition, which is central to the video's educational content. The limit is what the function approaches, not necessarily what the function equals at the point of interest.

💡Epsilon-Delta Definition

The Epsilon-Delta definition is a formal way to express the concept of a limit in mathematics. It states that the limit of a function as x approaches a certain point is a specific value if for any given tolerance level (Epsilon), there exists a corresponding proximity level (Delta) such that the function's value is within Epsilon of the limit whenever the input is within Delta of the point. The script provides an in-depth explanation of this definition and uses it to prove certain limits.

💡Tolerance

In the context of the Epsilon-Delta definition, tolerance refers to the acceptable distance from the limit that the function's value can be without violating the definition of the limit. Epsilon is used to represent this tolerance level. The script explains that for any given Epsilon, there must exist a Delta such that the function's value stays within this tolerance as x approaches the limit point.

💡Limit Point

A limit point, in the domain of a function, is a value towards which the function's input can approach. The script specifies that for the limit of a function to be defined, the point C does not need to be within the domain of the function (i.e., the function does not need to be defined at C), but C must be a limit point of the domain.

💡Domain

The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. In the script, it is mentioned that the domain element x must be within Delta of the limit point C, emphasizing the importance of the domain in the context of defining limits.

💡Negation of the Definition

The negation of the definition is a way to express what it means for a function not to have a particular limit. The script explains that to prove a function does not have a limit, one must show that there exists some tolerance Epsilon for which no matter how close x is forced to the limit point C, the function's value will not stay within the tolerance Epsilon of the alleged limit.

💡Neighborhood

In the script, a neighborhood is used to describe a region around a point within which certain conditions must be met. Specifically, for the Epsilon-Delta definition, a Delta neighborhood of C is a set of points within a distance Delta from the limit point C, and an Epsilon neighborhood of the limit L is a set of values within a distance Epsilon from the limit value L.

💡Proof

A proof in mathematics is a logical argument that establishes the truth of a statement. In the context of the script, proofs are provided to demonstrate that the limit of a function at a particular point is a specific value using the Epsilon-Delta definition. The script walks through the process of proving limits for simple functions like 4x + 1 and x^2.

💡Scratch Work

Scratch work refers to the preliminary calculations or reasoning done before writing a formal proof. The script mentions scratch work as an essential step in proving limits using the Epsilon-Delta definition, where one assumes the desired conclusion and works backward to find a suitable value for Delta.

💡Rational Function

A rational function is a function that can be expressed as the ratio of two polynomials. In the script, a practice exercise is provided where the function f(x) is a rational function, and the task is to prove that the limit of this function as x approaches 3 is 24. This serves as an example of applying the Epsilon-Delta definition to more complex functions.

Highlights

Introduction to the rigorous definition of continuity and the limit of a function, emphasizing the importance of a formal definition for mathematical precision.

Explanation of the Epsilon-Delta definition of the limit of a function, which is central to understanding continuity in calculus.

Clarification that the limit of a function does not depend on the value of the function at the limit point, but rather its behavior as it approaches the point.

Illustration of the Epsilon-Delta definition with visual aids to enhance understanding of the mathematical concept.

Discussion on the negation of the limit definition, explaining what it means for a function not to have a particular limit.

Introduction of the concept of 'neighborhoods' in the context of the Epsilon-Delta definition to describe the proximity of function values to the limit.

Emphasis on the fact that the limit point C does not need to be in the domain of the function for the limit to be defined.

Explanation of how the limit definition is independent of the function's value at the limit point, focusing on the approach to the point rather than the point itself.

Demonstration of the process of proving the limit of a function using the Epsilon-Delta definition, with an example of a linear function.

Presentation of a methodical approach to 'scratch work' in limit proofs, showing how to derive an appropriate Delta value.

Proof of the limit for a quadratic function, showcasing the process of manipulating expressions to fit the Epsilon-Delta criteria.

Introduction of a common scenario in limit proofs where multiple restrictions on Delta are necessary, using the minimum function to satisfy all conditions.

Finalization of the proof for the quadratic function limit, reinforcing the understanding of the Epsilon-Delta definition in practice.

Offering a practice exercise for viewers to apply the Epsilon-Delta definition to prove the limit of a rational function, encouraging active learning.

Provision of hints and a walkthrough for the practice exercise, aiding viewers in constructing their own proofs and deepening their comprehension.

Conclusion summarizing the importance of understanding the Epsilon-Delta definition for proving properties of functions and defining continuity.

Transcripts

Browse More Related Video

Precise Definition of a Limit - Example 1 Linear Function

Epsilon-delta limit definition 1 | Limits | Differential Calculus | Khan Academy

Epsilon-Delta Proof (Quadratic)

Calculus 1: The Epsilon-Delta Definition of the Limit

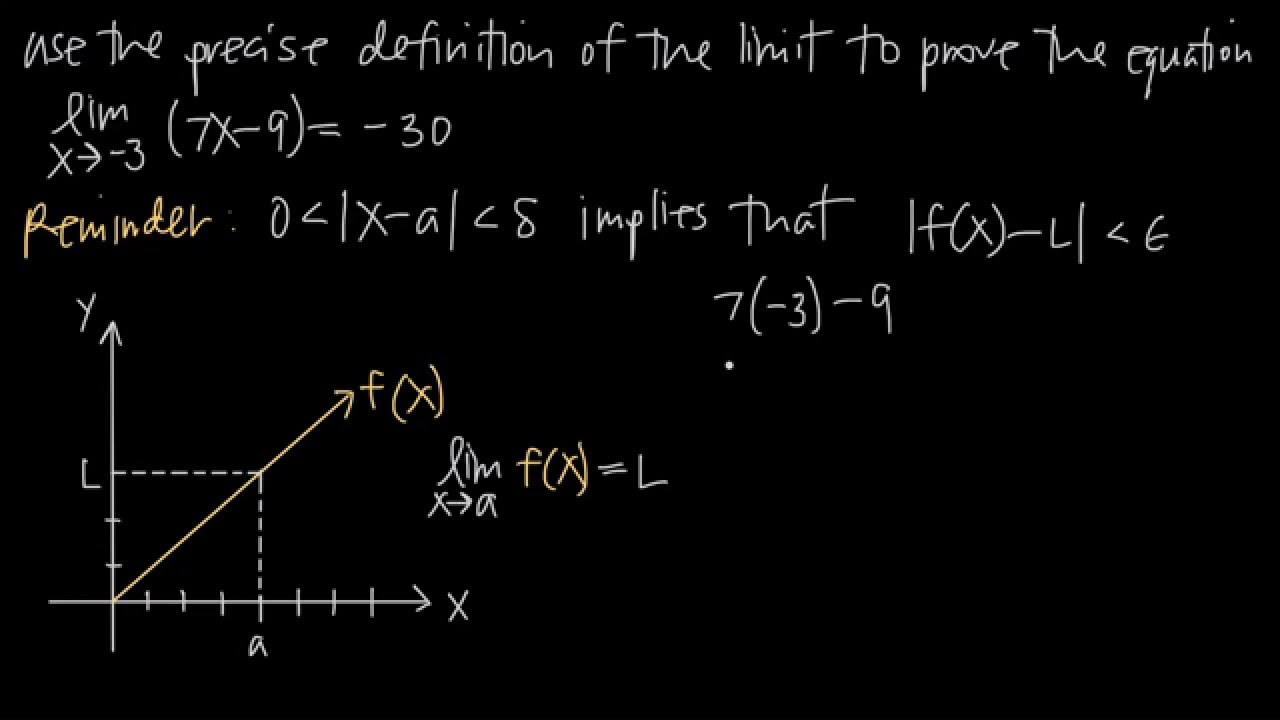
The precise definition of the limit EXPLAINED! (KristaKingMath)

This is the Epsilon Delta Definition of Continuity | Real Analysis

Related Tags

Epsilon Delta Function Limits Continuity Real Analysis Mathematics Calculus Limit Proofs Educational Concept Clarification Learning Resource