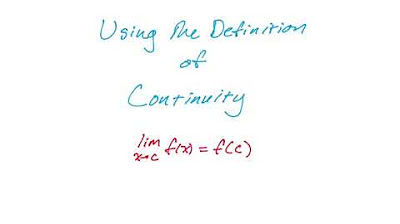This is the Epsilon Delta Definition of Continuity | Real Analysis
TLDRThis video script delves into the concept of continuity in calculus, offering a detailed explanation of the epsilon-delta definition of continuity. It clarifies that a function is continuous at a point if the limit of the function as x approaches that point equals the function's value at that point. The script also presents various characterizations of continuity, including a topological definition and a sequential definition, which is particularly useful for proving discontinuity. The video culminates with a proof demonstrating the continuity of the identity function and touches on the properties of continuous functions, such as their additive and multiplicative properties, concluding with an exercise to prove the continuity of the square root function.
Takeaways
- 📚 A function is considered continuous at a point if the limit of the function as X approaches a certain point C is equal to the function's value at that point C.
- 🔍 The Epsilon Delta definition is a rigorous formulation of continuity, stating that for any given Epsilon > 0, there exists a Delta > 0 such that if the distance between X and C is less than Delta, then the distance between f(X) and f(C) is less than Epsilon.
- 📈 The definition of continuity does not require C to be a limit point of the domain, simplifying the case when C is not a limit point, as the function is guaranteed to be continuous at C.
- 📝 There are four characterizations of continuity, including the Epsilon Delta definition, the topological or neighborhood definition, the limit definition, and the sequential definition.
- 🔄 The sequential definition is particularly useful for proving a function is not continuous at a point, by showing that a sequence converging to C does not result in the sequence of function values converging to f(C).
- 📉 The identity function f(X) = X is an example used to illustrate a simple Epsilon Delta continuity proof, showing it is continuous on its entire domain, the real numbers.
- 🔢 Continuity properties allow us to deduce that operations such as multiplication by a constant, addition, and composition with other continuous functions will result in a continuous function at a point C.
- 📐 Polynomial functions are continuous on their entire domain because they can be constructed using the identity function and applying continuity properties.
- 📘 Rational functions, which are quotients of polynomials, are continuous wherever they are defined, provided the denominator is not zero.
- 📌 An exercise is provided to prove that the square root function, f(X) = √X, is continuous on its domain, the non-negative real numbers.
- 🎓 The video script encourages viewers to support the channel on Patreon and offers additional resources and lessons for further understanding of continuity and related mathematical concepts.
Q & A
What is the epsilon-delta definition of continuity for a function?
-A function f is continuous at a point C if for all epsilon greater than zero, there exists some delta greater than zero such that for all x in the domain where x is within delta of C, the distance between f(x) and f(C) is less than epsilon.
Why is the epsilon-delta definition considered rigorous in mathematics?
-The epsilon-delta definition is rigorous because it provides a precise way to quantify the closeness of a function's value at a point to its limit, using the concepts of epsilon and delta which are based on the formal definition of a limit.
What is the relationship between the limit of a function and its continuity at a point?
-A function is continuous at a point if the limit of the function as x approaches that point is equal to the function's value at that point. Continuity is essentially a specific case of the limit concept where the function's value and its limit coincide.
Why is it important to consider whether C is a limit point of the domain when defining continuity?
-The limit point consideration is important because the definition of a limit requires x to approach C within the domain. If C is not a limit point, there is no approach within the domain, and the function is trivially continuous at C since x can only equal C, making f(x) - f(C) equal to zero.
What are the different characterizations of continuity mentioned in the script?
-The script mentions four characterizations: the epsilon-delta definition, the topological or neighborhood definition, the sequential definition, and the limit definition (only equivalent when C is a limit point of the domain).
How is the sequential definition of continuity different from the epsilon-delta definition?
-The sequential definition states that a function is continuous at a point if for all sequences that converge to that point within the domain, the sequence of images under the function also converges to the function's value at that point. It differs in that it does not require dealing with epsilons and deltas.
Can you provide an example of a function that is continuous on its entire domain?
-Yes, the identity function f(x) = x is an example of a function that is continuous on its entire domain, which is the set of all real numbers.
What is the significance of proving that a function like f(x) = x is continuous on its entire domain?
-Proving that a simple function like f(x) = x is continuous on its entire domain is significant because it allows us to use properties of continuity to show that more complex functions, such as polynomials and rational functions, are also continuous on their respective domains.
What is the exercise given at the end of the script for the viewer to try?
-The exercise is to prove that the function f(x) = sqrt(x) is continuous on its domain, which is the set of non-negative real numbers.
How can the properties of continuity be used to show that every polynomial is continuous?
-Since the identity function f(x) = x is continuous, and we know that the sum, difference, product, and quotient (where defined) of continuous functions are also continuous, we can use these properties to show that polynomials, which are sums and products of powers of x, are continuous on their entire domain.
Outlines
📚 Introduction to Continuity and Epsilon-Delta Definition
This paragraph introduces the concept of continuity in calculus, emphasizing the epsilon-delta definition. It explains that a function is continuous at a point C if the limit of the function as X approaches C is equal to the function's value at C. The paragraph also mentions that understanding functional limits is crucial for grasping the concept of continuity. The speaker provides a link to a lesson on limits for those who need a refresher and outlines the video's content, which includes the epsilon-delta definition, equivalent characterizations of continuity, and an epsilon-delta continuity proof. The importance of C being a limit point of the domain in the context of limits and continuity is highlighted, with the note that if C is not a limit point, the function is trivially continuous at C.
🔍 Exploring Characterizations of Continuity and a Continuity Proof Example
The second paragraph delves into different characterizations of continuity, including the epsilon-delta definition, the topological or neighborhood definition, and the sequential definition. It clarifies that all these definitions are equivalent except for the limit definition, which only applies when C is a limit point of the domain. The paragraph also discusses the ease of proving non-continuity using sequences. The speaker then provides a step-by-step example of proving the identity function (f(x) = x) is continuous over the entire real number domain using the epsilon-delta definition, demonstrating how to choose an appropriate Delta value to ensure the function's values stay within the epsilon tolerance of f(C).
📘 Properties of Continuous Functions and an Exercise
In the final paragraph, the speaker outlines the properties of continuous functions, such as the continuity of a constant multiple of a function, the sum, and the product of continuous functions. The paragraph uses these properties to argue that polynomials and rational functions are continuous over their respective domains. An exercise is presented for the viewer to prove the continuity of the square root function (f(x) = √x) over the non-negative reals, with a hint to first consider the case where C equals zero and then focus on positive numbers, potentially using a conjugate. The speaker encourages viewers to check out linked lessons for more continuity proofs and offers support through Patreon.
Mindmap
Keywords
💡Continuous
💡Epsilon-Delta Definition
💡Limit
💡Domain
💡Identity Function
💡Polynomial
💡Rational Function
💡Neighborhood
💡Sequence
💡Conjugate
Highlights
Introduction to the concept of continuity in calculus and its importance in understanding limits.
Rigorous definition of continuity using the Epsilon Delta definition and its relation to the limit of a function.
Explanation of the necessity for the limit point C to be within the domain for the definition of continuity to apply.
Clarification that if C is not a limit point of the domain, the function is trivially continuous at C.
Introduction of four different characterizations of continuity, including the Epsilon Delta definition and the sequential definition.
Discussion on the equivalence of the different definitions of continuity, especially when C is a limit point of the domain.
Illustration of the Epsilon Delta definition with a visual representation of a function approaching a point C.
Explanation of the topological or neighborhood definition of continuity, rephrasing the inequalities into neighborhood notation.
Introduction of the sequential definition of continuity and its utility in proving discontinuity.
Demonstration of proving the identity function (f(x) = x) is continuous using the Epsilon Delta definition.
Use of the Epsilon Delta definition to establish that the distance between f(x) and f(C) is less than Epsilon.
Discussion of the properties of continuity, such as multiplying a continuous function by a constant or adding continuous functions.
Application of continuity properties to show that polynomials and rational functions are continuous on their domains.
Exercise challenge for the viewer to prove that the square root function (f(x) = √x) is continuous on the non-negative reals.
Offering a hint for the exercise, suggesting to first consider the case where C equals zero and then focus on positive numbers.
Encouragement for viewers to engage with the content, ask questions, and support the channel.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: