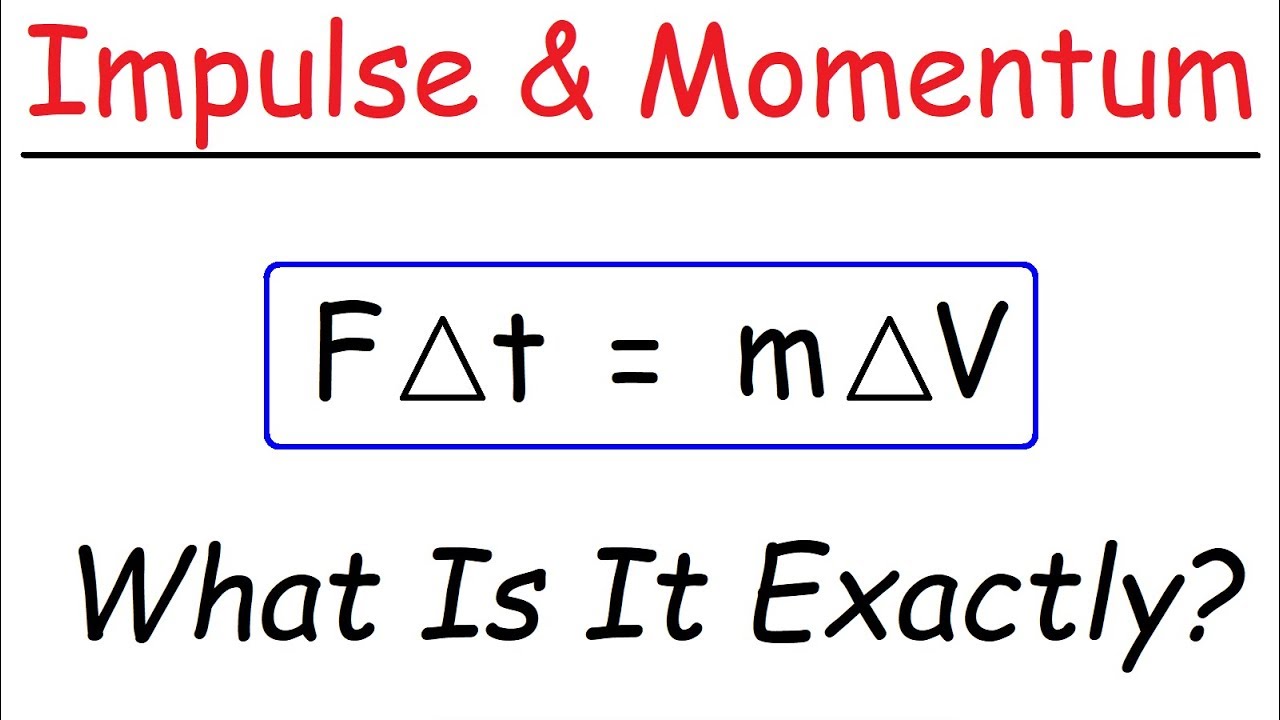High School Physics - Momentum & Impulse

Dan Fullerton

14 Nov 201106:24

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Mr. Fullerton explains the concepts of momentum and impulse with clarity and precision. He defines momentum as a vector quantity, measured in kilograms per second, and provides the formula P = mv. Using relatable examples like speeding cars and airplanes, he illustrates how to calculate momentum and the effects of changes in velocity on it. He then introduces impulse as the change in momentum (∆P = ∆J), emphasizing its vector nature and directionality. The video concludes with a practical problem-solving example, demonstrating how to find the final speed of an object after a collision, thus effectively engaging viewers and deepening their understanding of these fundamental physics concepts.

Takeaways

📌 Momentum is a measure of how difficult it is to stop an object and is a vector quantity with units of kilograms times meters per second (kg·m/s).
📌 The formula for momentum (P) is straightforward: P = mass (m) times velocity (v).
📌 Two objects with the same velocity will have momenta proportional to their masses; a more massive object has greater momentum.
📌 If an object's velocity is doubled, its momentum will also double, assuming mass remains constant.
📌 The momentum of an object can be calculated using its mass and velocity, as demonstrated with the example of a D3A bomber.
📌 Impulse (J) is the change in momentum (ΔP) of an object and is also a vector quantity, indicated by its direction.
📌 The impulse applied to an object can be calculated by finding the change in momentum (final momentum minus initial momentum).
📌 When an object comes to a halt, the impulse applied is equal in magnitude but opposite in direction to its initial momentum.
📌 An example of calculating the new speed of an object after an impulse is applied involves using the impulse and the object's mass to find the change in velocity.
📌 Impulse can be represented in Newton-seconds (N·s) and is used to describe the effect of a force applied over a period of time on an object's momentum.
📌 Understanding the concepts of momentum and impulse is crucial for predicting and analyzing the outcomes of collisions and other interactions between objects.

Q & A

What is the definition of momentum?
-Momentum is a measure of how hard it is to stop an object. It is a vector quantity, represented by the symbol P, and its units are kilograms times meters per second, which is equivalent to Newtons times a second.
What is the formula for calculating momentum?
-The formula for calculating momentum is P = m * v, where P is the momentum, m is the mass of the object, and v is its velocity.
How does the momentum of two objects with the same velocity but different masses compare?
-If two objects have the same velocity, the object with the larger mass will have a greater momentum. For example, if one object has twice the mass of another and they both have the same velocity, the object with the larger mass will have twice the momentum.
What happens to the momentum of an object if its velocity is doubled?
-If the velocity of an object is doubled, its momentum will also double. This is because momentum is directly proportional to velocity, as shown in the momentum formula (P = m * v).
What is the momentum of a D3A bomber with a mass of 3600 kilograms and a velocity of 85 m/s due east?
-The momentum of the D3A bomber can be calculated using the formula P = m * v. With a mass of 3600 kilograms and a velocity of 85 m/s, the momentum is 3600 kg * 85 m/s, which equals 3.06 * 10^5 kg*m/s to the east.
After dropping its torpedo and attaining a cruising speed of 120 m/s, what is the new momentum of the D3A bomber with a reduced mass of 3000 kilograms?
-Using the momentum formula P = m * v, the new momentum of the D3A bomber with a mass of 3000 kilograms and a velocity of 120 m/s is 3000 kg * 120 m/s, which equals 3.6 * 10^5 kg*m/s east.
What is impulse, and how is it related to momentum?
-Impulse is the change in momentum of an object, represented by the symbol J. It is calculated as the final momentum minus the initial momentum (J = ΔP = P_final - P_initial). Impulse is also a vector quantity and has a direction associated with it.
If a D3A bomber with an initial momentum of 3.6 * 10^5 kg*m/s comes to a halt, what is the impulse applied to it?
-The impulse applied to the D3A bomber is the change in momentum, which is the final momentum (zero, since it stops) minus the initial momentum. Therefore, the impulse is -3.6 * 10^5 kg*m/s (negative because the direction is opposite to the initial eastward momentum).
How can you calculate the final velocity of a block after it experiences an impulse?
-To calculate the final velocity of a block after experiencing an impulse, you use the impulse formula J = ΔP = m * (v_final - v_initial). By solving for v_final (final velocity), you get v_final = (J + m * v_initial) / m.
A 6-kilogram block is sliding east with a momentum of 30 kg*m/s and strikes an obstacle. If the obstacle exerts an impulse of 10 N*s to the west, what is the block's final speed?
-Using the impulse formula J = m * Δv, where m is the mass, Δv is the change in velocity, and J is the impulse, the final speed can be found by (10 N*s + 6 kg * 5 m/s) / 6 kg, which results in a final speed of approximately 3.3 m/s.
What is the significance of the direction in momentum and impulse calculations?
-The direction is significant in momentum and impulse calculations because they are vector quantities. The direction indicates the axis or orientation in which the momentum or impulse is applied. For example, in the D3A bomber scenario, the momentum and impulse were specified as east or west to indicate the direction of motion and force application.

Outlines

00:00

🚗 Introduction to Momentum and Impulse

This paragraph introduces the concepts of momentum and impulse, explaining their importance in physics. Momentum is defined as a vector quantity that measures the difficulty of stopping an object, represented by the formula P = mass × velocity, with units of kilograms meters per second. The example of a car speeding at 27 meters per second illustrates the significant momentum and the impossibility of stopping it with one's hand. The paragraph further explains how momentum can be calculated for different scenarios, such as two trains with different masses but the same velocity, and a D3A bomber taking off and dropping a torpedo. It also introduces the concept of impulse as a change in momentum (ΔP = J), which is a vector and has a direction, using the D3A bomber coming to a halt as an example to demonstrate the calculation of impulse.

05:02

💥 Collision Impulse Calculation

This paragraph delves into the calculation of impulse during a collision. It begins with a scenario where a 6-kilogram block with a momentum of 30 kilogram meters per second east collides with an obstacle. The obstacle exerts an impulse of 10 Newton seconds to the west. The paragraph explains how to use the definition of impulse (J = ΔP) to find the final velocity of the block after the collision. By considering the mass and the change in velocity, the paragraph provides a step-by-step breakdown of the calculation, leading to a final velocity of approximately 3.3 meters per second. This example demonstrates the practical application of impulse in understanding changes in momentum during collisions.

Mindmap

Keywords

💡momentum

Momentum is a measure of the quantity of motion an object possesses, defined as the product of the object's mass and velocity. In the context of the video, it is a vector quantity, meaning it has both magnitude and direction, and is calculated using the formula P = mv. The video emphasizes the concept by illustrating how a car moving at high velocity has a significant amount of momentum, making it nearly impossible to stop with one's hand.

💡impulse

Impulse is the change in momentum of an object, represented by the symbol J and is also a vector quantity. It is calculated as the final momentum minus the initial momentum (ΔP = P_final - P_initial). The video uses the concept of impulse to explain how forces applied over time can change an object's momentum, such as bringing a speeding car to a halt or a D3A bomber coming to rest on the ground.

💡vector quantity

A vector quantity is one that has both magnitude and direction. In the context of the video, both momentum and impulse are vector quantities, meaning they are represented by arrows that show the size and direction of the force. This is important in physics as it helps to understand how different forces can combine or cancel each other out.

💡mass

Mass is a measure of the amount of matter in an object, typically measured in kilograms. In the video, mass is a critical factor in calculating momentum and impulse, as it is multiplied by velocity to determine an object's momentum. Changes in mass can also lead to changes in momentum, which is reflected in the impulse.

💡velocity

Velocity is a measure of the speed of an object in a specific direction. It is a vector quantity and is essential in the calculation of both momentum and impulse. The video emphasizes the impact of velocity on momentum, showing that if the velocity of an object doubles, its momentum also doubles.

💡Newton

A Newton is the SI unit of force and is defined as the force required to accelerate a one-kilogram mass by one meter per second squared. In the context of the video, the unit of momentum is kilograms meters per second, which is equivalent to Newtons times a second. This highlights the connection between momentum and force.

💡collision

A collision is an event in which two or more objects come into contact with each other, often resulting in a transfer of momentum and energy. In the video, collisions are discussed in the context of impulse, where the force exerted over a short period changes the momentum of the objects involved.

💡frictionless surface

A frictionless surface is an idealized concept in physics where an object can move without any resistance. This simplifies the analysis of motion as it eliminates the effects of frictional forces. In the video, the concept is used to describe a scenario where a block slides on a horizontal surface without any friction, allowing for a clear demonstration of momentum and impulse changes during a collision.

💡formula

A formula in physics is a mathematical expression that represents a relationship between different physical quantities. In the video, several formulas are introduced, such as the formula for momentum (P = mv) and the calculation of impulse (J = ΔP). These formulas are essential for understanding and calculating the changes in an object's motion due to applied forces.

💡direction

Direction refers to the path or line along which something moves or points. In physics, direction is a crucial aspect of vector quantities like momentum and impulse. The video emphasizes the importance of direction in understanding how these quantities can add or subtract depending on whether they are in the same or opposite directions.

💡stop

Stopping refers to bringing an object from a state of motion to rest. In the context of the video, stopping is used to illustrate the concept of impulse, as it involves applying a force over time to change the momentum of an object to zero.

Highlights

Momentum is a vector quantity that measures the difficulty of stopping an object.

The symbol for momentum is P and its units are kilograms times meters per second, which is equivalent to Newtons times a second.

The formula for momentum is straightforward: momentum equals mass times velocity.

Two objects with the same velocity but different masses will have different momenta; the object with the greater mass will have a greater momentum.

Doubling the velocity of an object with a given mass will result in doubling its momentum.

An example of calculating momentum is provided with a D3A bomber that has a mass of 3600 kilograms and departs from its aircraft carrier with a velocity of 85 m/s due east.

After dropping its torpedo, the D3A bomber's mass decreases to 3000 kilograms and its cruising speed becomes 120 meters per second, changing its momentum accordingly.

Impulse is defined as the change in momentum (ΔP) and is represented by the symbol J.

Impulse is also a vector quantity and has a direction associated with it, which is determined by the change in direction of the momentum.

In the case of the D3A bomber coming to a halt, the impulse applied is equal to the negative change in momentum, which is directed westward since the plane was initially moving east.

A six-kilogram block sliding eastward on a frictionless surface with a momentum of 30 kilogram meters per second provides an example of calculating the change in momentum after a collision.

The impulse exerted by an obstacle on the six-kilogram block is 10 Newton-seconds to the west, resulting in a change in velocity after the collision.

The final velocity of the block after the collision can be calculated using the impulse and the initial momentum, resulting in a velocity of approximately 3.3 meters per second.

The concepts of momentum and impulse are essential in understanding the dynamics of moving objects and the forces that act upon them.

These principles have practical applications in various fields, including physics, engineering, and sports.

Understanding momentum and impulse can help in predicting outcomes in collisions and designing systems that can safely decelerate or stop objects.

The relationship between mass, velocity, and momentum is fundamental to the study of classical mechanics and is used to solve a wide range of problems in the field.

Transcripts

Browse More Related Video

Introduction to Impulse & Momentum - Physics

College Physics 1: Lecture 26 - Impulse and Momentum

2022 Live Review 5 | AP Physics 1 | Understanding Impulse and Momentum

IGCSE Physics [Syllabus 1.6] Momentum

What Are Momentum and Impulse? | Physics in Motion

High School Physics - Impulse-Momentum Theorem

High School Physics - Momentum & Impulse

Takeaways

Q & A

What is the definition of momentum?

What is the formula for calculating momentum?

How does the momentum of two objects with the same velocity but different masses compare?

What happens to the momentum of an object if its velocity is doubled?

What is the momentum of a D3A bomber with a mass of 3600 kilograms and a velocity of 85 m/s due east?

After dropping its torpedo and attaining a cruising speed of 120 m/s, what is the new momentum of the D3A bomber with a reduced mass of 3000 kilograms?

What is impulse, and how is it related to momentum?

If a D3A bomber with an initial momentum of 3.6 * 10^5 kg*m/s comes to a halt, what is the impulse applied to it?

How can you calculate the final velocity of a block after it experiences an impulse?

A 6-kilogram block is sliding east with a momentum of 30 kgm/s and strikes an obstacle. If the obstacle exerts an impulse of 10 Ns to the west, what is the block's final speed?