College Physics 1: Lecture 26 - Impulse and Momentum

Spahn's Science Lectures

18 Nov 202231:53

EducationalLearning

32 Likes 10 Comments

TLDRIn this physics lecture, the concept of impulse and momentum is explored, focusing on their relationship and application to collisions. Impulse is defined as the area under the force versus time graph during a collision, and its unit is Newton-second, though kilogram meter per second is preferred for consistency with momentum. Momentum, mass times velocity, is introduced as a vector quantity, and the Impulse-Momentum Theorem (J = Δp) is highlighted, illustrating how impulse leads to a change in momentum. Examples, including a rubber ball bouncing and a sled's speed change with rocket thrust, demonstrate the theorem's practical use. The lecture concludes with an emphasis on the theorem's significance and its application in real-world scenarios, such as the strategy of hedgehogs to cushion falls and the technique of catching water balloons.

Takeaways

🚀 Impulse and Momentum are key concepts in physics, particularly relevant during collisions where objects interact briefly.
🔍 Impulse is defined as the area under the force versus time graph during a collision and is represented by the letter 'J'.
📊 The impulse can be calculated using the average force applied over the duration of the collision, simplifying the process without needing integral calculus.
⚖️ Impulse has units of Newton-seconds (N·s), but the preferred unit is kilogram-meters per second (kg·m/s), aligning with the units of momentum.
📚 Momentum is defined as mass times velocity (p = mv) and is a vector quantity, having both magnitude and direction.
🔄 The Impulse-Momentum Theorem states that the impulse applied to an object is equal to the change in its momentum (J = Δp).
🛡️ Hedgehogs use the principle of impulse and momentum to reduce impact by landing on their cushioned spines, increasing the collision time and decreasing the average force.
🎈 Catching a water balloon gently by following through with the motion can increase the collision time, thus reducing the force exerted on the balloon and preventing it from bursting.
📉 The equation Δp/Δt equals the average force experienced during a collision highlights the relationship between collision time and force.
📚 An example problem demonstrates how to use the Impulse-Momentum Theorem to calculate the final velocity of a sled with rocket engines, emphasizing the theorem's practical applications.
📝 The lecture concludes with questions that reinforce the understanding of impulse, momentum, and their vector nature, emphasizing the importance of direction in calculations.

Q & A

What is the primary focus of the lecture?
-The lecture primarily focuses on the concept of momentum and its relation to impulse, Newton's Second Law, and the conservation of momentum in physics.
What is considered a collision in the context of this lecture?
-A collision is defined as a brief interaction between objects, which can involve two or more objects colliding at the same time.
How is the impulse during a collision typically represented in the lecture?
-The impulse during a collision is represented as a force that changes over a short duration, often quite large, and is depicted as an increasing and then decreasing force on a force versus time graph.
What is the definition of impulse in the context of physics?
-Impulse is defined as the area under the force versus time graph during a collision, and it is represented by the letter J.
How can the impulse be simplified for calculation purposes?
-The impulse can be simplified by considering an average force applied over the same duration as the actual changing force, creating a rectangle under the force versus time graph whose area can be easily calculated.
What are the units of impulse and why is kilogram meter per second preferred?
-The units of impulse are Newton second, but the preferred unit is kilogram meter per second because it matches the units of momentum, simplifying calculations and comparisons.
What is the relationship between impulse and momentum?
-The relationship between impulse and momentum is given by the impulse-momentum theorem, which states that the impulse delivered to an object is equal to the change in its momentum (Δp).
Why is the equation Δp/ΔT significant in real-world applications?
-The equation Δp/ΔT is significant because it implies that increasing the time of a collision (ΔT) will decrease the average force experienced during the collision, which has practical applications in safety and impact reduction.
Can you provide an example from the lecture that illustrates the impulse-momentum theorem?
-An example from the lecture is the hedgehog falling from a tree. By curling into a ball and landing on its spines, the hedgehog increases the time of collision, which according to the impulse-momentum theorem, reduces the average force of the impact and cushions the fall.
What is the final speed of a 500 kg sled coasting at 20 m/s that turns on its rocket engines for 5 seconds with a thrust of 1000 Newtons?
-Using the impulse-momentum theorem, the final speed of the sled is calculated by adding the initial velocity (20 m/s) to the change in velocity caused by the thrust (1000 N * 5 s / 500 kg), resulting in a final speed of 30 m/s.

Outlines

00:00

📚 Introduction to Impulse and Momentum

The lecture begins with an introduction to the concepts of impulse and momentum, which are pivotal in understanding collisions. It emphasizes that momentum is a fundamental concept in physics, related to impulse and Newton's Second Law. The lecture also introduces the idea of conservation laws and how momentum is conserved. The material is connected to previous topics, with a focus on the force experienced during collisions and how it changes over time, defining impulse as the area under the force versus time graph.

05:02

📐 Calculating Impulse and Average Force

This paragraph delves into the calculation of impulse, which is defined as the area under the force curve over time. It simplifies the concept by introducing the idea of an average force over the same time period, leading to a rectangle whose area can be easily calculated. The unit of impulse is derived from the units of force and time, resulting in Newton-seconds or, more commonly, kilogram meters per second. The paragraph also clarifies that impulse is a vector and discusses its directionality. An example problem is presented, involving a rubber ball bouncing off the floor, to illustrate the calculation of impulse and average force.

10:03

🚀 The Impulse-Momentum Theorem

The paragraph explains the relationship between force, impulse, and momentum during a collision. It expands on Newton's Second Law to show that the impulse (the average force times the time interval) is equal to the change in momentum (final momentum minus initial momentum). This leads to the Impulse-Momentum Theorem, which states that the impulse applied to an object is equal to the change in its momentum. The units of momentum are discussed, highlighting the importance of using kilogram meters per second as the unit for both impulse and momentum, ensuring consistency in calculations.

15:06

🧲 Understanding Momentum as Mass Times Velocity

The concept of momentum (P) is defined as the product of an object's mass (M) and its velocity (V), resulting in the unit of kilogram meters per second. The paragraph emphasizes that momentum is a vector quantity, having both magnitude and direction. It provides a table to give students a sense of the momentum values for various objects, ranging from a falling raindrop to a car on the highway, to help them understand the concept better. The Impulse-Momentum Theorem is simplified to J = ΔP, showing that impulse results in a change in momentum.

20:09

🛡️ Applications of the Impulse-Momentum Theorem

The lecture discusses real-world applications of the Impulse-Momentum Theorem, particularly how increasing the time of a collision can decrease the force experienced. Examples include hedgehogs falling from trees and the act of catching water balloons. The theorem is then applied to a problem involving a sled with a rocket engine, showing how to calculate the final speed after the engine is turned on for a certain duration. The problem illustrates the practical use of the theorem in determining the change in velocity due to an applied force over time.

25:12

🔍 End of Lecture Questions

The lecture concludes with questions that test the understanding of impulse and momentum. The first question involves comparing two force versus time graphs to determine which one delivers a greater impulse. The second question asks for the calculation of the change in momentum (Δp) for a cart, emphasizing the importance of considering direction in vector calculations. The answers are provided, with a reminder to be mindful of the vector nature of momentum and the impact of direction on calculations.

Mindmap

Keywords

💡Impulse

Impulse is defined as the product of the average force applied over the time interval during which it acts. In the context of the video, impulse is crucial for understanding what happens during collisions. It is represented by the letter 'J' and is calculated as the area under the force versus time graph. The video emphasizes that impulse is a vector quantity, meaning it has both magnitude and direction, and it is directly proportional to the change in momentum of an object.

💡Momentum

Momentum is a fundamental concept in physics, defined as the product of an object's mass and its velocity (MV). It is a vector quantity, indicating that it has direction as well as magnitude. The video explains that momentum is conserved in a closed system and is central to understanding the effects of collisions. It is also highlighted that the unit of momentum is kilogram meters per second, which is consistent with the unit of impulse, emphasizing their relationship.

💡Collision

A collision, as discussed in the video, is a brief interaction between objects. It is a key scenario where the concepts of impulse and momentum become significant. During a collision, objects experience forces that can change their state of motion, compressing and then expanding. The video uses collisions to illustrate the application of impulse and momentum, such as when a soccer ball is kicked.

💡Newton's Second Law

Newton's Second Law relates force, mass, and acceleration by stating that the force acting on an object is equal to the mass of the object times its acceleration (F = ma). In the video, this law is expanded to include the concept of impulse and is used to derive the relationship between impulse and change in momentum. It is a fundamental principle that underpins the discussion on how forces impact the motion of objects.

💡Conservation Laws

Conservation laws are principles stating that certain quantities remain constant throughout a process. In the video, it is mentioned that the concept of momentum conservation is a significant conservation law in physics. This law implies that the total momentum of a closed system of objects remains constant if no external forces are acting upon it, which is a key idea introduced towards the end of the script.

💡Force

Force is a push or pull upon an object resulting from its interaction with another object. In the video, force is described in the context of collisions, where it can be delivered over a short duration and is often quite large. The concept of 'impulse force' is introduced, which is a strong but quick force experienced during a collision, and its effect is analyzed through the graph of force versus time.

💡Average Force

Average force is the constant force that has the same effect as the actual varying force applied over a certain time period. The video explains that instead of dealing with the complex calculation of the area under a curve (which would require calculus), one can simplify the problem by considering an average force that results in the same impulse as the actual force applied during a collision.

💡Compression

Compression, in the context of the video, refers to the temporary change in shape or size of an object when it is subjected to a force. During a collision, objects will compress and then expand back to their original shape. The video uses the concept of compression to explain how the force experienced by an object increases during the collision until it reaches maximum compression.

💡Impulse Momentum Theorem

The Impulse Momentum Theorem is a principle derived from Newton's Second Law, stating that the impulse applied to an object is equal to the change in its momentum (J = Δp). The video emphasizes this theorem as it shows the direct relationship between the impulse delivered to an object and the resulting change in its momentum, which is a fundamental concept for analyzing collisions and forces applied over time.

💡Vector

A vector is a quantity that has both magnitude and direction. In the video, both impulse and momentum are described as vector quantities. This means that when calculating these values, one must consider not only how large they are but also the direction in which they act. The video illustrates this with examples such as the direction of the force applied during a collision and the direction of an object's velocity.

Highlights

Introduction to the concept of impulse and momentum in relation to collisions.

Impulse is defined as the brief interaction force during collisions, which can be more complex than a single value.

The graph of force versus time during a collision shows how force changes over a short duration.

Impulse is calculated as the area under the force versus time graph, which can be simplified using average force.

Impulse has units of Newton Seconds, but kilogram meter per second is preferred for consistency with momentum units.

Momentum is defined as mass times velocity (MV) and is a vector quantity.

The impulse-momentum theorem states that impulse (J) equals change in momentum (Δp).

Increasing the time of a collision can decrease the average force experienced, as demonstrated by hedgehogs falling from trees.

The equation Δp/ΔT shows the relationship between collision time and average force.

Example problem: Calculating impulse and average force on a bouncing rubber ball.

The importance of understanding the direction of vectors when calculating momentum.

A table of different objects and their average momentum to provide perspective on expected values.

The application of the impulse-momentum theorem in real-world scenarios like catching water balloons.

Solving an example problem involving a sled's change in velocity due to rocket engine thrust.

End of lecture questions to test understanding of impulse, momentum, and their applications.

Conclusion and transition to the next lecture topic: conservation of momentum.

Transcripts

Browse More Related Video

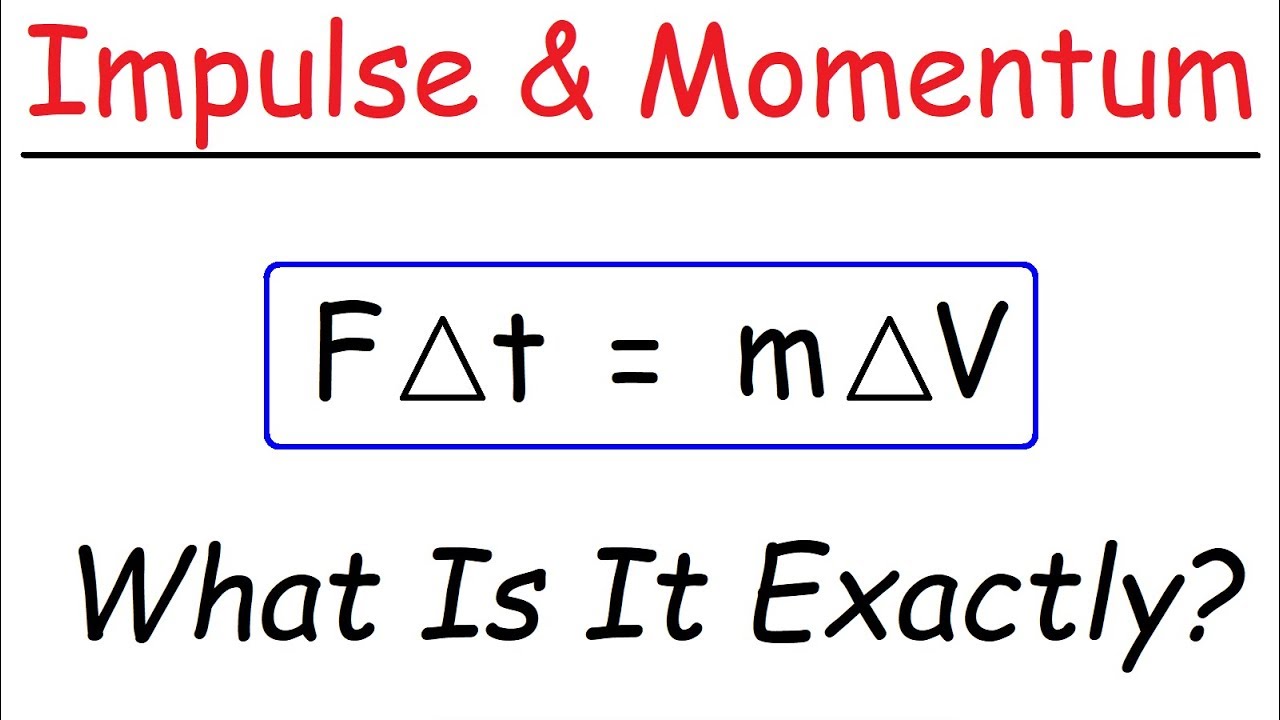
Introduction to Impulse & Momentum - Physics

2022 Live Review 5 | AP Physics 1 | Understanding Impulse and Momentum

High School Physics - Impulse-Momentum Theorem

High School Physics - Momentum & Impulse

College Physics 1: Lecture 27 - Conservation of Momentum

What Are Momentum and Impulse? | Physics in Motion

Related Tags

Impulse Momentum Physics Collision Conservation Laws Newton's Second Law Force Velocity Education