Conservation of energy | Work and energy | Physics | Khan Academy
TLDRIn this video, we explore the concept of potential and kinetic energy through a practical example. We start with a 1-kilogram object held 10 meters above the ground on Earth, calculating its potential energy using mgh. When released, the object’s potential energy converts to kinetic energy, demonstrating the conservation of energy. We further investigate the object's behavior on a frictionless ice ramp, showing how potential energy converts to kinetic energy at various points. This method simplifies complex calculations, illustrating energy conservation’s power in understanding motion and energy transformations.
Takeaways
- 📚 The script discusses the concept of gravitational potential energy and its conversion to kinetic energy, using a 1 kg object held 10 meters above the ground as an example.
- 🌍 The importance of specifying the planet (Earth in this case) is highlighted because gravity varies from one celestial body to another.
- 📉 The potential energy formula is mgh, where m is mass, g is the acceleration due to gravity, and h is height.
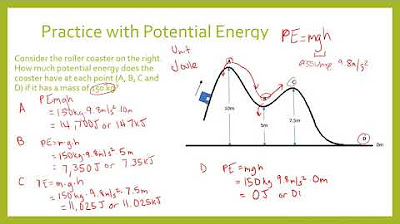
- 🔢 The potential energy of the object at 10 meters height is calculated to be 100 joules, assuming an acceleration due to gravity (g) of 10 m/s² for simplicity.
- 💥 When the object is released, it begins to fall and accelerate due to gravity, converting potential energy into kinetic energy.
- 🏗️ The potential energy at the point of impact with the ground is zero because the height (h) is zero, demonstrating the conservation of energy principle.
- 🚀 The kinetic energy formula, \( rac{1}{2}mv^2 \), is used to calculate the velocity of the object just before it hits the ground, resulting in approximately 14.1 m/s.
- 🛷 The script introduces a scenario where the object slides down an icy ramp instead of falling straight, emphasizing the utility of energy concepts in non-straightfall situations.
- 🛤️ The velocity of the object sliding down the icy ramp is determined to be the same as if it had fallen straight down, illustrating the conservation of energy in different contexts.
- 🔄 The conservation of energy principle is applied to calculate the velocity of the object at various points along the slide, including halfway down where potential and kinetic energies are equal.
- 📚 The script concludes by emphasizing the practicality of energy concepts over traditional kinematics in solving complex problems involving changing angles and surfaces.
Q & A
What is the significance of the 1 kilogram object in the video?
-The 1 kilogram object serves as a reference point to demonstrate the concepts of gravitational potential energy, kinetic energy, and the conservation of energy in different scenarios.
Why is the height of 10 meters mentioned in the script?
-The height of 10 meters is used to calculate the potential energy of the 1 kilogram object when it is held above the ground, which is essential for understanding the energy transformations in the scenarios presented.
What is the assumed acceleration due to gravity in the script?
-The script assumes an acceleration due to gravity of 10 meters per second squared for simplicity, instead of the actual 9.8 m/s² on Earth.
How is the potential energy calculated in the script?
-The potential energy is calculated using the formula mgh, where m is the mass (1 kg), g is the acceleration due to gravity (10 m/s²), and h is the height (10 meters), resulting in 100 joules.
What happens to the potential energy when the object is released?
-When the object is released, the potential energy is converted into kinetic energy due to the object's acceleration towards the ground.
How is the kinetic energy of the object determined right before it hits the ground?
-Since the potential energy at the ground level is zero, all the initial potential energy (100 joules) is converted into kinetic energy, which is then used to calculate the object's velocity using the kinetic energy formula 1/2 mv².
What is the velocity of the object right before it touches the ground?
-The velocity of the object right before it touches the ground is approximately 14.1 meters per second, calculated from the kinetic energy equation.
Why is the concept of energy conservation important in the script?
-The concept of energy conservation is important because it allows for the analysis of energy transformations in different scenarios, such as when the object falls straight down or slides down an icy ramp.
How does the script use energy conservation to solve for the object's velocity on an icy ramp?
-By recognizing that the total energy (initial potential energy) remains constant and converting it entirely to kinetic energy at the bottom of the ramp, the script calculates the object's horizontal velocity without needing complex kinematic equations.
What is the significance of the icy ramp in the script's demonstration?
-The icy ramp serves as an example of a non-straight path for the object's fall, illustrating how energy conservation can simplify the analysis of motion in complex scenarios, such as calculating the object's velocity at different points along the ramp.
How does the script demonstrate the calculation of velocity at a specific point on the icy ramp?
-The script calculates the velocity at a specific point on the ramp by determining the remaining potential energy at that height, converting it to kinetic energy, and then solving for the velocity using the kinetic energy formula.
Outlines
🌍 Gravity and Potential Energy
The script begins by revisiting a scenario from a previous video where a 1-kilogram object is held 10 meters above the ground on Earth. The potential energy (PE) is calculated using the formula mgh, where m is mass, g is the acceleration due to gravity (assumed to be 10 m/s² for simplicity), and h is height. The object has 100 joules of PE at this height. When the object is released, it begins to fall, accelerating due to gravity. The script emphasizes the law of conservation of energy, stating that energy cannot be created or destroyed but can change forms. As the object falls, its PE is converted into kinetic energy (KE). The formula for KE is 1/2 mv², and by equating the lost PE to the gained KE, the velocity of the object just before it hits the ground is calculated to be approximately 14.1 m/s. The script then introduces a variation of the scenario where the object slides down an icy ramp instead of falling straight, setting up the next part of the discussion.
🛷 Energy Conversion on an Icy Ramp
In the second paragraph, the script introduces a new scenario where the 1-kilogram object slides down an icy ramp instead of falling directly. The object starts with the same 100 joules of PE at a height of 10 meters. As it slides down, the PE is gradually converted into KE. The script simplifies the calculation of the object's velocity at different points along the ramp by using the conservation of energy principle. It demonstrates that at the bottom of the ramp, where the height is 0, all of the PE has been converted into KE, resulting in a velocity of 14.1 m/s horizontally. The script then shows how to calculate the velocity at a point halfway down the ramp, where the height is 5 meters. The PE at this point is 50 joules, which has also been converted into KE, leading to a velocity of 10 m/s. The use of energy conservation makes these calculations straightforward, even when dealing with a continuously changing slope, which would be complex to solve using traditional kinematics.
Mindmap
Keywords
💡Potential Energy
💡Kinetic Energy
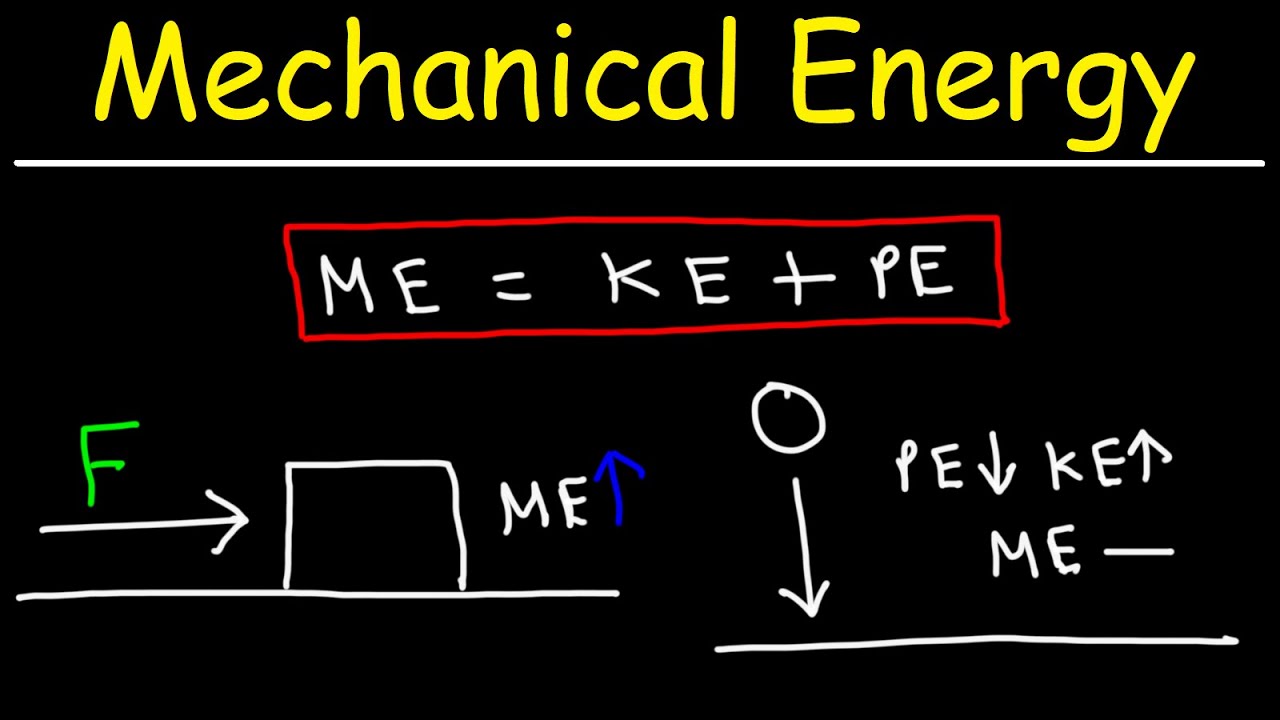
💡Conservation of Energy
💡Acceleration Due to Gravity
💡Mass
💡Height
💡Velocity
💡Ice Ramp
💡Friction
💡Kinematics
💡Vector
Highlights
Introduction of a 1-kilogram object held 10 meters above the ground to illustrate gravitational potential energy.
Assumption of Earth's gravitational acceleration as 10 m/s² for simplified calculations.
Calculation of potential energy (mgh) resulting in 100 joules when the object is held at height.
Explanation of potential energy becoming zero when the object is at ground level due to zero height.
Introduction of the law of conservation of energy, emphasizing energy conversion rather than destruction.
Conversion of gravitational potential energy into kinetic energy as the object falls.
Use of kinetic energy formula (1/2 mv²) to calculate the object's velocity before impact.
Determination of the object's velocity at 14.1 m/s just before hitting the ground.
Demonstration of energy concepts to solve problems that would be difficult with traditional kinematics.
Setup of a scenario with the object sliding down an icy ramp to explore energy transformation.
Explanation of how frictionless ice allows for total energy conservation in the system.
Calculation of kinetic energy when the object is halfway down the ramp, with height reduced to 5 meters.
Determination of the object's velocity at 10 m/s at the midpoint of the slide using conservation of energy.
Illustration of how energy principles simplify the calculation of velocities at various points on a slope.
Highlighting the practical applications of energy conservation in solving complex motion problems.
Teaser for the next video, promising further exploration of energy concepts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: