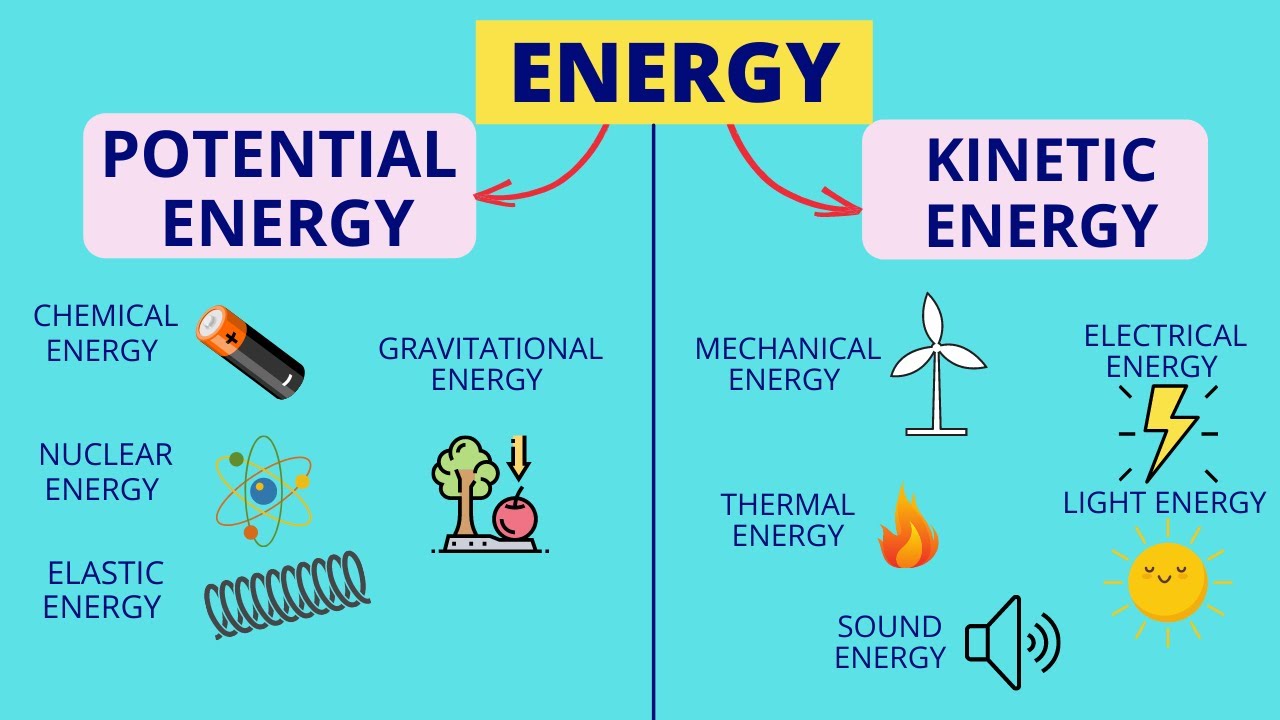
Kinetic Energy and Potential Energy
TLDRThis video delves into the concepts of kinetic and potential energy, explaining kinetic energy as the energy of motion and potential energy as stored energy due to position or condition. It covers the formulas for gravitational potential energy (mgh) and kinetic energy (1/2 mv^2), and illustrates how potential energy converts to kinetic energy as an object falls. The video also touches on elastic potential energy, providing an example with springs and their constants, and hints at other forms of potential energy like chemical and electric potential energy.
Takeaways
- 🏃 Kinetic energy is the energy of motion; any object in motion has kinetic energy.
- 📐 The formula for kinetic energy is KE = 0.5 * m * v^2, where m is mass in kilograms and v is speed in meters per second.
- 📈 Doubling the mass of an object doubles its kinetic energy, while doubling the speed quadruples it.
- 🔄 If an object's mass is tripled and its speed is quadrupled, the kinetic energy increases by a factor of 48.
- 🌐 Potential energy is stored energy due to an object's position, typically related to gravity.
- 📉 Gravitational potential energy is calculated using the formula mgh, where m is mass, g is gravitational acceleration (9.8 m/s^2), and h is height above the ground.
- 🏀 An example: A 10 kg ball 50 meters above the ground has 4900 Joules of gravitational potential energy.
- 🚀 As an object falls, its potential energy decreases while its kinetic energy increases, conserving total mechanical energy.
- 🏃♂️ At the lowest point before impact, all potential energy is converted to kinetic energy.
- 🔋 Elastic potential energy is stored in objects like springs and is calculated using the formula 0.5 * k * x^2, where k is the spring constant and x is the displacement from equilibrium.
- 🔌 Other forms of potential energy include chemical energy, electric potential energy, and more, which may be covered in different physics courses.
Q & A
What is kinetic energy?
-Kinetic energy is the energy of motion. It represents the energy an object possesses due to its movement. Anything that moves has kinetic energy, and it depends on the object's mass and speed.
How is kinetic energy calculated?
-The formula for calculating kinetic energy (KE) is KE = 0.5 * m * v^2, where m is the mass of the object in kilograms and v is its speed in meters per second. When using these units, the kinetic energy is measured in joules.
What happens to an object's kinetic energy if its mass is doubled?
-If an object's mass is doubled, its kinetic energy will also double, assuming its speed remains constant. This is because the mass (m) is raised to the first power in the kinetic energy formula.
How does doubling the speed of an object affect its kinetic energy?
-Doubling the speed of an object quadruples its kinetic energy. This is because the speed (v) is squared in the kinetic energy formula, so increasing v by a factor of 2 results in an increase by a factor of 2^2, which is 4.
What is potential energy?
-Potential energy is a form of stored energy due to an object's position. It represents the energy an object has because of its location, typically in a gravitational field, and can be converted into kinetic energy.
What is the formula for gravitational potential energy?
-The formula for gravitational potential energy (PE) is PE = m * g * h, where m is the mass in kilograms, g is the gravitational acceleration (approximately 9.8 m/s^2), and h is the height above the ground level in meters.
How does the potential energy of an object change when it falls from a height?
-As an object falls from a height, its potential energy decreases because it is losing height. Simultaneously, its kinetic energy increases as it accelerates towards the ground. The potential energy is converted into kinetic energy during the fall.
At what point is all the potential energy converted to kinetic energy?
-All the potential energy is converted to kinetic energy when the object reaches the lowest point in its trajectory, just before it hits the ground or comes to rest.
What is the speed of a 10 kg ball falling from a height of 50 meters?
-The speed of a 10 kg ball falling from a height of 50 meters can be calculated using the conservation of energy principle. The ball's potential energy at the top (mgh) is equal to its kinetic energy at the bottom (0.5 * m * v^2). By solving the equation, we find that the ball's speed just before impact is approximately 31.3 meters per second.
What is elastic potential energy?
-Elastic potential energy is the energy stored in an object when it is stretched or compressed, like a spring. The formula for elastic potential energy is PE = 0.5 * k * x^2, where k is the spring constant and x is the displacement from the equilibrium position.
How does the spring constant (k) affect the stiffness of a spring?
-The spring constant (k) indicates the stiffness of a spring. A higher spring constant means the spring is stiffer and requires more force to stretch or compress it by a given distance. Conversely, a lower spring constant means the spring is looser and can be stretched or compressed more easily.
What are some other forms of potential energy?
-Other forms of potential energy include chemical potential energy (stored in chemical bonds), electric potential energy (stored based on a charge's position in an electric field), and nuclear potential energy (stored due to the forces within atomic nuclei).
Outlines
🏃 Kinetic Energy Fundamentals
This paragraph introduces the concept of kinetic energy, explaining it as the energy of motion. It emphasizes that any object in motion possesses kinetic energy, and its magnitude depends on the object's mass and velocity. The formula for kinetic energy (KE = 1/2 mv^2) is presented, with m being mass and v being velocity. The paragraph also discusses how changes in mass and velocity affect kinetic energy, providing examples of doubling the mass or speed and explaining the resulting changes in kinetic energy. A typical physics exam question is used to illustrate this concept.
📈 Grasping Gravitational Potential Energy
The second paragraph delves into gravitational potential energy (PE), which is energy due to an object's position. It uses the example of two objects at different heights to illustrate that the higher object has more PE. The formula for gravitational PE (mgh) is introduced, with m being mass, g being gravitational acceleration, and h being height. The paragraph then calculates the PE of a 10 kg ball 50 meters above the ground, resulting in 4900 joules. It explains the energy transformation as the ball falls from its initial position to just before it hits the ground, converting PE into kinetic energy.
🔄 Elastic Potential Energy and Energy Conservation
The final paragraph discusses another form of potential energy, elastic potential energy, which is stored when a force is applied to compress or stretch a spring. The formula for elastic potential energy (1/2 kx^2) is presented, with k being the spring constant and x the displacement from equilibrium. The paragraph explains the concept of the spring constant and how it relates to the stiffness of the spring. It concludes by mentioning other forms of potential energy, such as chemical and electric potential energy, and encourages viewers to explore more complex problems through provided links.
Mindmap
Keywords
💡Kinetic Energy
💡Potential Energy
💡Energy Conservation
💡Gravitational Acceleration
💡Elastic Potential Energy
💡Spring Constant
💡Energy Transformation
💡Velocity
💡Acceleration
💡Height
💡Mass
Highlights
Introduction to kinetic energy as energy in motion.
Explanation of kinetic energy's dependence on mass and speed, with formula KE = 1/2 m v^2.
Demonstration of how doubling the mass or speed affects kinetic energy.
Advanced example of calculating kinetic energy change with mass and speed variations.
Introduction to potential energy as stored energy due to position.
Explanation of gravitational potential energy with formula PE = mgh.
Comparison of potential energy between two objects at different heights.
Detailed calculation of gravitational potential energy for a specific example.
Discussion on the conversion of potential energy to kinetic energy during free fall.
Explanation of kinetic energy at the moment before impact with the ground.
Demonstration of calculating the speed of an object just before it hits the ground using conservation of energy.
Introduction to elastic potential energy and its formula.
Explanation of the spring constant and its significance in elastic potential energy.
Comparison of loose and stiff springs based on their spring constants.
Brief mention of other forms of potential energy, like chemical and electric potential energy.
Closing remarks encouraging further exploration of kinetic and potential energy problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: