AP Physics 1 Energy Review
TLDRThis video script offers a comprehensive review of the concept of energy in the context of AP Physics 1. It delves into the definition of work and its relationship with energy, explaining how work can change an object's energy through mechanisms such as force and displacement. The script elaborates on the different forms of energy, including kinetic and potential energy, with a focus on gravitational and elastic potential energy. It also introduces the conservation of mechanical energy and the work-energy theorem, highlighting the importance of understanding energy transformations in various physical scenarios, such as collisions and friction. The video concludes with an example problem that illustrates the application of energy conservation principles in analyzing the motion of a block on a ramp and its interaction with a spring.
Takeaways
- 🔨 Work is defined as the product of force (F) and displacement (D) in the direction of the force, measured in joules (J).
- 📐 The work done (W) is given by the equation W = F * D * cos(theta), where theta is the angle between the force and displacement vectors.
- 🔄 Positive work (W > 0) increases an object's energy, while negative work (W < 0) decreases it.
- 🏃 Kinetic energy (KE) is the energy of motion, proportional to the mass (m) and the square of velocity (v^2).
- 🌐 Gravitational potential energy (PE) depends on the object's mass, height (h), and the gravitational field strength (g), calculated as PE = m * g * h.
- 🔋 Elastic potential energy (EPE) is stored energy in objects like springs or rubber bands due to elastic deformation, given by EPE = (1/2) * k * x^2, where k is the spring constant and x is the displacement.
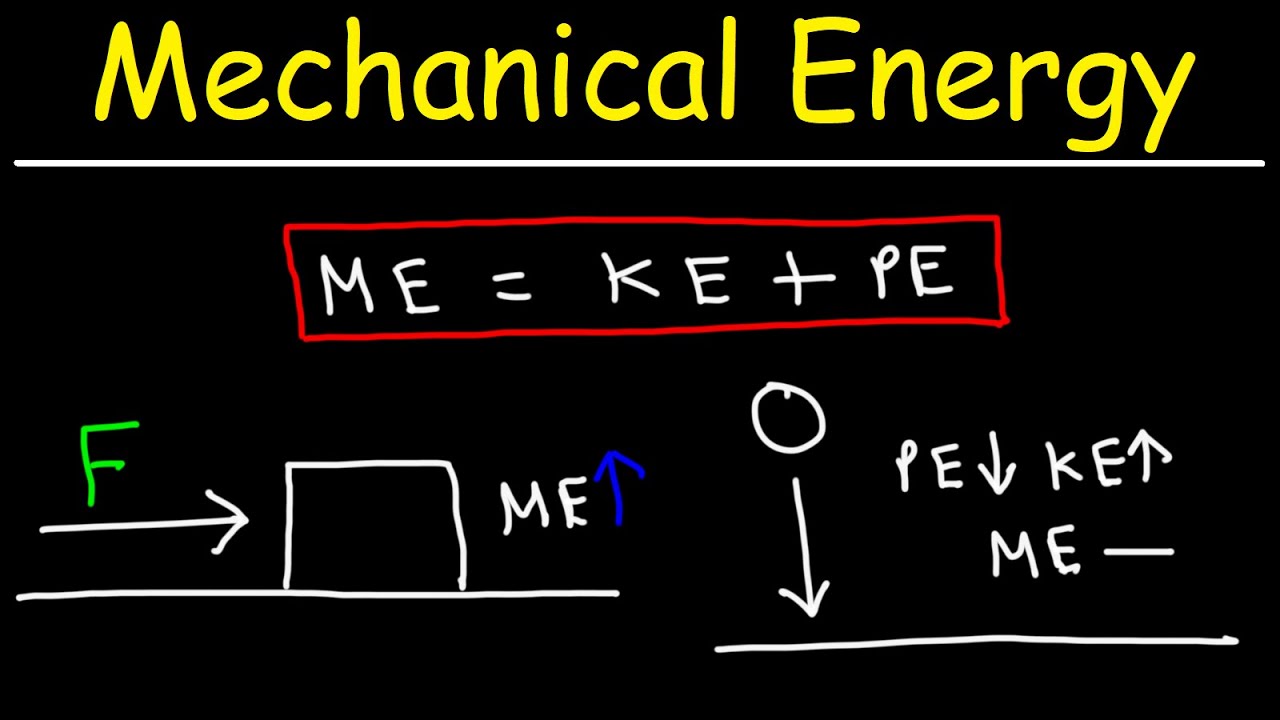
- ⚖️ Mechanical energy is the sum of kinetic and potential energies and is conserved in isolated systems without non-conservative forces.
- 🚀 Conservation of mechanical energy can be expressed as initial energy (E_i) equals final energy (E_f), or ΔE = 0.
- 🌡️ Non-conservative forces like friction can lead to energy loss in the form of heat or sound, affecting the conservation of mechanical energy.
- 📉 In the presence of non-conservative forces, the work-energy theorem states that the change in energy (ΔE) is equal to the work done on the system.
- 🔄 Energy transformations: Gravitational potential energy can be converted to kinetic energy, and vice versa, but other forms of energy (sound, heat) can also be involved in the process.
Q & A
What is the definition of work in the context of physics?
-In physics, work is defined as the product of the force exerted on an object and the distance the object moves in the direction of the force. If a force F causes an object to move through a distance D, then work is being done on that object.
How is work calculated and what units are used for measurement?
-Work is calculated using the formula W = F * D * cos(theta), where W is work, F is the force in Newtons, D is the distance in meters, and theta is the angle between the force and the displacement vector. Work is measured in joules.
What are the conditions for work to be positive or negative?
-Work is positive when the angle between the force and the displacement is between 0 and 90 degrees, which results in an increase in the object's energy. Work is negative when the angle is between 90 and 180 degrees, leading to a decrease in the object's energy.
What is kinetic energy and how is it related to an object's speed?
-Kinetic energy is the energy of an object due to its motion. It is proportional to the square of the object's speed (V^2) and also depends on the object's mass. If the speed of an object doubles, its kinetic energy increases by a factor of four, assuming mass remains constant.
Explain the concept of gravitational potential energy.
-Gravitational potential energy is the energy an object possesses due to its position in a gravitational field. It depends on the object's mass, the height above a reference point, and the strength of the gravitational field. The higher an object is lifted in a gravitational field, the more gravitational potential energy it has.
How is elastic potential energy related to the stretching or compressing of an object?
-Elastic potential energy is the energy stored in an object when it is stretched or compressed, like a rubber band or a spring. It is proportional to the square of the amount of stretching or compressing (X^2) and is associated with the spring constant (k). When an object is released after being stretched or compressed, this energy is converted into kinetic energy as it returns to its original shape.
What is mechanical energy and how is it calculated?
-Mechanical energy is the sum of an object's kinetic and potential energies. It is often represented as 'E' for the total energy of a system and can include both gravitational and elastic potential energy. Mechanical energy is conserved in a system when no external non-conservative forces act on it.
What is the work-energy theorem and how does it relate to the conservation of energy?
-The work-energy theorem states that the change in energy of an object or a system is equal to the work done on it. If the change in energy is zero, then the mechanical energy is conserved. This theorem connects the work done by forces on a system to the resulting change in energy, whether it be an increase or decrease in kinetic or potential energy.
How does friction affect the conservation of mechanical energy in a system?
-Friction is a non-conservative force that can do work on an object, leading to a change in the system's mechanical energy. When friction does work, it converts mechanical energy into other forms of energy, such as heat, which results in a loss of mechanical energy and thus, the mechanical energy is not conserved in the presence of friction.
What are the different forms of energy that can result from a loss of kinetic energy in a system?
-A loss of kinetic energy in a system can result in the gain of potential energy, but it can also convert into other forms of energy like sound, heat, or deformation. For example, during a collision, kinetic energy can be transformed into the deformation of objects, sound through vibrations in the air, and heat due to friction between surfaces.
How can energy conservation be applied to solve problems involving objects moving down a ramp and colliding with a spring?
-Energy conservation can be applied by analyzing the initial and final energies of the object and the work done by non-conservative forces like friction. By equating the initial gravitational potential energy with the sum of the final kinetic energy and the elastic potential energy stored in the spring, one can solve for unknowns such as the compression distance of the spring or the speed of the object at various points in the motion.
Outlines
🔧 Work and Energy Fundamentals in Physics
This paragraph introduces the concept of work in the context of physics, defining it as the product of force and displacement (FD) when the force causes movement. It explains that work is measured in joules and is associated with changes in an object's energy. The discussion then expands to include the more accurate work equation, FD cosine theta, highlighting the importance of the angle between the force and displacement vectors. The paragraph also distinguishes between positive and negative work, relating them to increases and decreases in energy, respectively.
🏃♂️ Kinetic and Gravitational Potential Energy
The second paragraph delves into different forms of energy, focusing on kinetic and gravitational potential energy. Kinetic energy is described as the energy due to an object's motion, with its magnitude proportional to the square of the object's velocity. Gravitational potential energy is explained as the energy due to an object's position in a gravitational field, which depends on the object's mass, the height, and the strength of the gravitational field. The paragraph emphasizes that these forms of energy are scalars and measured in joules, and introduces the concept of mechanical energy as the sum of kinetic and potential energies.
📈 Gravitational Potential Energy and Conservation Laws
This paragraph further explores gravitational potential energy, discussing its expression when gravitational acceleration is not constant over large distances. It introduces the concept of negative potential energy and explains how it relates to the proximity of objects. The paragraph then discusses the conservation of energy, emphasizing that the mechanical energy of an object is conserved in the absence of non-conservative forces. It also touches on the importance of defining the system correctly in energy conservation problems.
🌐 Elastic Potential Energy and Energy Transformation
The fourth paragraph focuses on elastic potential energy, which arises from the stretching or compressing of objects like rubber bands or springs. It explains how this form of energy is proportional to the square of the amount of stretching or compressing. The paragraph also addresses the conservation of energy, particularly in scenarios where mechanical energy is conserved, and introduces the work-energy theorem, which relates the work done on an object to the change in its energy. It highlights the role of non-conservative forces in energy transformation and the various forms energy can take, such as sound, heat, or deformation.
⚙️ Energy Equations and Power
The final paragraph discusses the application of energy equations, especially in situations where acceleration is not constant. It contrasts the use of kinematic equations with energy equations, emphasizing the latter's versatility. The concept of power is introduced as the rate of energy usage or work done, measured in watts. The paragraph concludes with an example problem involving a block on a ramp, a level track, and a spring, illustrating how energy transformations and conservation principles can be applied to understand the system's dynamics.
Mindmap
Keywords
💡Work
💡Energy
💡Kinetic Energy
💡Gravitational Potential Energy
💡Elastic Potential Energy
💡Conservation of Energy
💡Mechanical Energy
💡Power
💡Non-Conservative Forces
💡Cosine Theta
Highlights
Work is defined as the product of force and the distance moved by an object in the direction of the force.
Work is measured in joules when force is in Newtons and distance in meters.
The work equation W = F * D * cos(theta) accounts for the angle between the force and displacement vectors.
Positive work increases an object's energy, while negative work decreases it.
Kinetic energy is the energy of motion, proportional to the mass of an object and the square of its velocity.
Gravitational potential energy depends on an object's mass, height, and the strength of the gravitational field.
Elastic potential energy is stored in objects like rubber bands or springs when they are stretched or compressed.
Mechanical energy is the sum of kinetic and potential energies.
Conservation of mechanical energy applies when only conservative forces, like gravity, act on a system.
The work-energy theorem relates the work done on an object to the change in its energy.
Energy can be converted into various forms, including sound, heat, and deformation.
Kinematic equations are limited to scenarios with constant acceleration, unlike energy equations which can handle variable acceleration.
In collisions, energy is not only converted between kinetic and potential forms but can also be lost as sound, heat, or deformation.
Friction is a non-conservative force that can do negative work, converting energy into heat.
The conservation of energy principle states that the total energy in an isolated system remains constant, assuming no external non-conservative forces.
Power is the rate at which work is done or energy is transferred, measured in watts.
When an object falls down a ramp, its gravitational potential energy is converted into kinetic energy, with some loss due to friction.
In an example problem, a block falling down a ramp, compressing a spring, and colliding with it, demonstrates energy conservation and transformation.
The block cannot return to its original height after falling and compressing a spring due to energy loss in the process.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: