Mole Conversions Made Easy: How to Convert Between Grams and Moles

ketzbook
4 Mar 201707:15
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video by Ketzbook introduces the concept of mole conversions in chemistry, explaining the mole as a unit that represents 6.02 x 10^23 entities, useful for counting atoms. It demonstrates how to calculate the molar mass of elements and compounds and convert between moles and grams using lithium as an example. The video also covers calculating molar mass for molecules like carbon monoxide, nitrogen gas, and carbon dioxide, as well as ionic compounds like magnesium nitrate. It guides viewers through step-by-step mole conversion problems, emphasizing the importance of the molar mass as a conversion factor.

Takeaways
  • 🧪 A mole in chemistry is a large number of things, similar to a dozen but much larger, equaling 6 x 10^23 entities.
  • 📏 The mole concept is used because atoms are extremely small, making it impractical to count them individually.
  • 💧 An example given is that one cup of water contains about 15 trillion trillion hydrogen atoms, which is equivalent to 25 moles of hydrogen atoms.
  • ⚖️ The molar mass is the mass of one mole of a substance, measured in grams per mole (g/mol), and serves as a conversion factor between grams and moles.
  • 🌐 The number of atoms in one gram of an element is 6 x 10^23, which is why 1 mole equals this number of entities.
  • 📊 To find the moles of an element in grams, divide the mass (in grams) by the molar mass of the element.
  • 🔢 For converting moles to grams, multiply the number of moles by the molar mass of the element.
  • 🌡️ The molar mass of a compound is calculated by adding the molar masses of all the atoms in the molecule.
  • 📘 For diatomic molecules like N2, the molar mass is twice the atomic mass of nitrogen.
  • 🧪 For ionic compounds, calculate the molar mass by summing the molar masses of all constituent elements, considering their quantities in the formula.
  • 📚 The script provides step-by-step examples for converting between grams and moles for elements like lithium, and compounds like magnesium nitrate.
Q & A

  • What is a mole in the context of chemistry?

    -In chemistry, a mole is a large number of things, similar to a dozen but much larger. One mole is 6 times 10 to the 23rd things, which is approximately 600 billion trillion items. It is used to count atoms, molecules, and other chemical entities.

  • Why is the number of 6 times 10 to the 23rd significant in chemistry?

    -The number 6 times 10 to the 23rd is significant because it represents the number of atoms in 12 grams of carbon-12, which is the standard for defining atomic mass units (amu). This number is also used to define a mole, making it a convenient way to count atoms by weighing them.

  • What is the molar mass of lithium, and how does it relate to its atomic weight?

    -The molar mass of lithium is 6.94 grams per mole, which is also its atomic weight. This means that one lithium atom has an average mass of 6.94 amu, and one mole of lithium atoms has a mass of 6.94 grams.

  • How can you calculate the number of moles of lithium in 25 grams of lithium?

    -To calculate the number of moles of lithium in 25 grams, you would use the molar mass of lithium (6.94 grams per mole) as a conversion factor. Divide 25 grams by 6.94 grams/mole, resulting in approximately 3.6 moles of lithium.

  • What is the abbreviation for mole, and why is it written without the 'e'?

    -The abbreviation for mole is 'mol'. It is written without the 'e' as a convention in chemistry, which also happens to save time and effort in writing.

  • How do you find the mass of 11.5 moles of lithium?

    -To find the mass of 11.5 moles of lithium, use the molar mass of lithium (6.94 grams/mole) as a conversion factor. Multiply 11.5 moles by 6.94 grams/mole, which equals 79.8 grams of lithium.

  • What is the molar mass of a molecule, and how is it calculated?

    -The molar mass of a molecule is the total mass of one mole of that molecule. It is calculated by adding up the molar masses of all the atoms within the molecule.

  • What is the molar mass of carbon monoxide (CO), and how do you calculate it?

    -The molar mass of carbon monoxide (CO) is 28.01 grams per mole. It is calculated by adding the molar mass of one carbon atom (12.01 grams/mole) to the molar mass of one oxygen atom (16 grams/mole).

  • How do you calculate the molar mass of a diatomic molecule like nitrogen (N2)?

    -To calculate the molar mass of nitrogen (N2), which is a diatomic molecule, you multiply the molar mass of one nitrogen atom (14.01 grams/mole) by 2, resulting in a molar mass of 28.02 grams per mole for N2.

  • What is the molar mass of carbon dioxide (CO2), and how is it determined?

    -The molar mass of carbon dioxide (CO2) is 44.01 grams per mole. It is determined by adding the molar mass of one carbon atom (12.01 grams/mole) and twice the molar mass of one oxygen atom (16 grams/mole), since there are two oxygen atoms in CO2.

  • How do you calculate the molar mass of an ionic compound like magnesium nitrate (Mg(NO3)2)?

    -To calculate the molar mass of magnesium nitrate (Mg(NO3)2), you add the molar mass of magnesium (24.3 grams/mole) to twice the molar mass of the nitrate ion (which includes 2 nitrogen atoms and 6 oxygen atoms). This calculation is 24.3 + (14.01 * 2) + (16 * 6), resulting in a molar mass of 148.3 grams per mole.

  • How can you convert 6.35 grams of magnesium nitrate to moles?

    -To convert 6.35 grams of magnesium nitrate to moles, use the molar mass of magnesium nitrate (148.3 grams/mole) as a conversion factor. Divide 6.35 grams by 148.3 grams/mole, which equals approximately 0.0428 moles.

  • What is the mass of 0.369 moles of magnesium nitrate?

    -To find the mass of 0.369 moles of magnesium nitrate, use the molar mass (148.3 grams/mole) as a conversion factor. Multiply 0.369 moles by 148.3 grams/mole, resulting in 54.7 grams of magnesium nitrate.

Outlines
00:00
🧪 Mole Conversions and Molar Mass Basics

This paragraph introduces the concept of moles in chemistry, explaining that a mole is a large number, equivalent to 6.022 x 10^23 entities, which is useful for counting atoms due to their small size. It uses the example of lithium to illustrate how molar mass, the mass of one mole of a substance, serves as a conversion factor between grams and moles. The viewer is guided through a problem calculating the number of moles in 25 grams of lithium and another problem determining the mass of 11.5 moles of lithium, emphasizing the process of unit conversion using molar mass as the conversion factor.

05:02
📚 Mole Conversions for Compounds and Calculation of Molar Mass

The second paragraph delves into mole conversions for compounds, starting with calculating the molar mass of molecules like carbon monoxide, nitrogen (N2), and carbon dioxide by summing the molar masses of their constituent atoms. It also covers ionic compounds, using magnesium nitrate as an example, to show how to calculate the molar mass by adding the molar masses of all atoms in the compound. The paragraph then applies these concepts to solve mole conversion problems, converting 6.35 grams of magnesium nitrate to moles and determining the mass of 0.369 moles of magnesium nitrate, reinforcing the use of molar mass as a conversion factor between grams and moles.

Mindmap
Keywords
💡Mole
In chemistry, a mole is a unit that represents a large number of entities, such as atoms, molecules, or ions. It is defined as 6.022 x 10^23 particles, which is the number of atoms in exactly 12 grams of carbon-12. The concept is central to the video's theme as it simplifies the counting of atoms and molecules, making it easier to work with the incredibly small and numerous particles in chemical reactions. For example, the script mentions that one mole of lithium atoms has a mass of 6.94 grams, which is the molar mass of lithium.
💡Molar Mass
Molar mass is the mass of one mole of a substance, typically expressed in grams per mole (g/mol). It is calculated by summing the atomic masses of all the atoms in a molecule or formula unit of a compound. The video explains the importance of molar mass in converting between the mass of a substance and the number of moles. For instance, the molar mass of lithium is given as 6.94 g/mol, which is used to determine how many moles are in a certain mass of lithium.
💡Atomic Mass Units (amu)
Atomic mass units (amu) are units used to express the mass of atoms, typically on the periodic table. One amu is defined as one twelfth of the mass of a carbon-12 atom. The video uses amu to explain the concept of molar mass, stating that one gram equals 6 x 10^23 amu, which helps in understanding the relationship between moles and grams.
💡Conversion Factor
A conversion factor is a ratio that relates two different but equivalent quantities, used to convert from one unit to another. In the context of the video, the molar mass serves as a conversion factor to change between grams and moles. For example, the script uses the molar mass of lithium (6.94 g/mol) as a conversion factor to calculate the number of moles in 25 grams of lithium.
💡Unit Conversion
Unit conversion is the process of changing a quantity from one unit of measure to another. The video demonstrates unit conversion in the context of chemical calculations, specifically converting between grams and moles using the molar mass as the conversion factor. The script illustrates this with problems involving lithium and magnesium nitrate.
💡Lithium
Lithium is a chemical element with the symbol Li and atomic number 3. It is used in the video as an example to explain the concept of molar mass and mole conversions. The script mentions lithium's atomic weight and molar mass, and uses it in problems to demonstrate how to calculate the number of moles in a given mass and vice versa.
💡Carbon Monoxide
Carbon monoxide (CO) is a compound consisting of one carbon atom and one oxygen atom. The video uses carbon monoxide to illustrate how to calculate the molar mass of a molecule by adding the molar masses of its constituent atoms (12.01 g/mol for carbon and 16 g/mol for oxygen), resulting in a molar mass of 28.01 g/mol for CO.
💡Nitrogen
Nitrogen is a diatomic gas under standard conditions, with the chemical formula N2, meaning it consists of two nitrogen atoms bonded together. The video explains that the molar mass of N2 is calculated by multiplying the atomic mass of nitrogen (14.01 g/mol) by 2, yielding a molar mass of 28.02 g/mol for nitrogen gas.
💡Carbon Dioxide
Carbon dioxide (CO2) is a compound composed of one carbon atom and two oxygen atoms. The video uses CO2 to demonstrate the calculation of molar mass for a molecule with more than one type of atom, resulting in a molar mass of 44.01 g/mol for carbon dioxide.
💡Ionic Compounds
Ionic compounds are formed by the electrostatic attraction between oppositely charged ions. In the video, magnesium nitrate (Mg(NO3)2) is used as an example of an ionic compound. The molar mass of magnesium nitrate is calculated by adding the molar masses of magnesium (24.3 g/mol), nitrogen (14.01 g/mol), and oxygen (16 g/mol), considering the number of each atom present in the formula.
💡Mg(NO3)2 (Magnesium Nitrate)
Magnesium nitrate is a salt consisting of magnesium ions (Mg2+) and nitrate ions (NO3-). The video uses magnesium nitrate to show how to calculate the molar mass of an ionic compound, which is 148.3 g/mol. This molar mass is then used as a conversion factor to convert between grams and moles of magnesium nitrate.
Highlights

A mole in chemistry is a large number of things, similar to a dozen but much larger.

One mole equals 6 times 10 to the 23rd things, which is 600 billion trillion items.

The mole is used to count atoms, molecules, and other chemicals due to their small size.

One gram equals 6 times 10 to the 23rd atomic mass units, relating to the definition of a mole.

The atomic weight of an element is also its molar mass, as shown with lithium having a molar mass of 6.94 grams.

Molar mass serves as a conversion factor between grams and moles.

Example problem: Calculating 3.6 moles of lithium from 25 grams using the molar mass.

The abbreviation of mole is MOL, omitting the 'e' to save writing energy.

Example problem: Finding the mass of 11.5 moles of lithium, resulting in 79.8 grams.

Molar mass of a molecule is calculated by adding the molar masses of all atoms in the molecule.

Carbon monoxide has a molar mass of 28.01 grams per mole, combining carbon and oxygen masses.

Nitrogen gas (N2) has a molar mass of 28.02 grams per mole, considering two nitrogen atoms.

Carbon dioxide's molar mass is 44.01 grams per mole, calculated from one carbon and two oxygen atoms.

For ionic compounds like magnesium nitrate, molar mass is the sum of the molar masses of all constituent atoms.

Magnesium nitrate has a molar mass of 148.3 grams per mole, used for mole to gram conversions.

Example: Converting 6.35 grams of magnesium nitrate to moles results in 0.0428 moles.

Example: Calculating the mass of 0.369 moles of magnesium nitrate gives 54.7 grams.

The video concludes with a call to action for likes, comments, subscriptions, and visiting the creator's website.

Transcripts

Browse More Related Video

Avogadro's Number, The Mole, Grams, Atoms, Molar Mass Calculations - Introduction

Step by Step Stoichiometry Practice Problems | How to Pass Chemistry

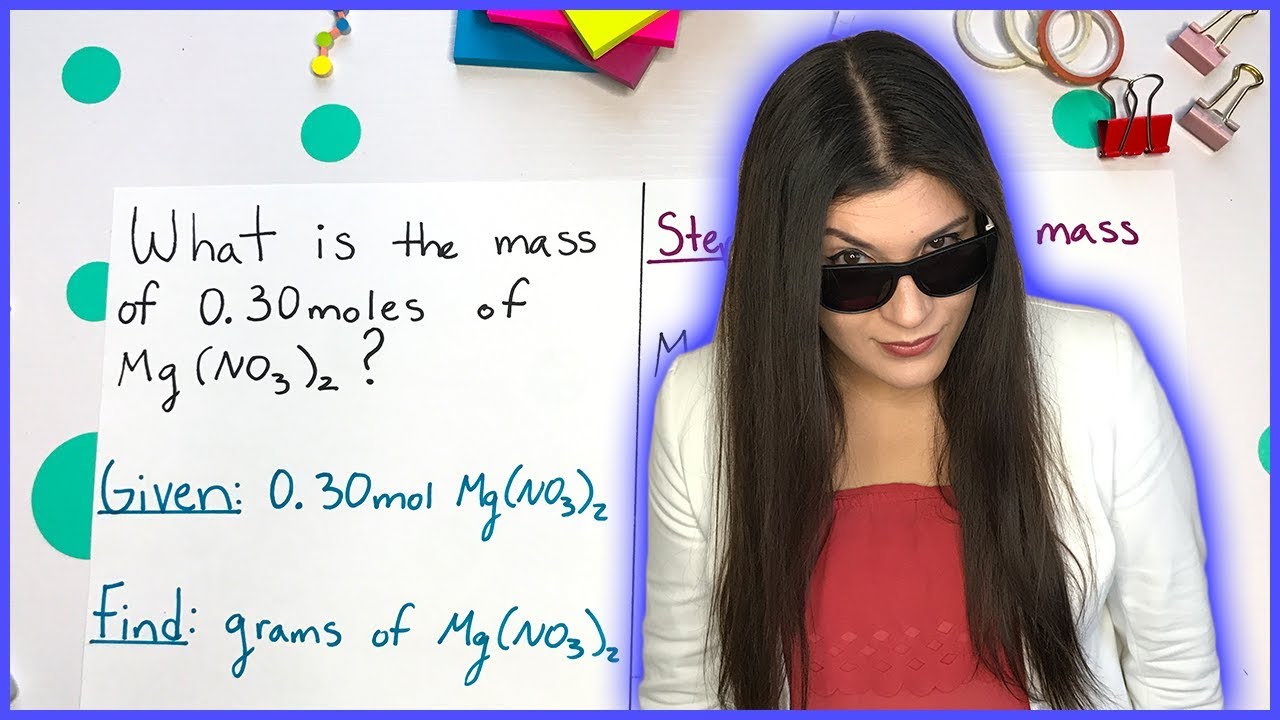
Converting Grams to Moles Using Molar Mass | How to Pass Chemistry

Very Common Mole Questions

02 - What is Avogadro's Number & the Mole in Chemistry? Part 1

GCSE Chemistry - The Mole (Higher Tier) #25

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Mole ConversionsChemistry TutorialMolar MassElemental AnalysisCompound CalculationScientific EducationAtomic WeightChemical CountingEducational VideoKetzbook