Lec 4 | MIT 18.01 Single Variable Calculus, Fall 2007
TLDRIn this educational video, Professor Haynes Miller, substituting for David Jerison, delves into the intricacies of calculus, focusing on differentiation rules. He explains the product rule, quotient rule, and chain rule with illustrative examples, demonstrating how to differentiate composite functions and products or quotients of functions. Miller also introduces higher derivatives, showcasing how repeated differentiation of sine and cosine functions returns to the original function, and provides the formula for the nth derivative of x^n, revealing the concept of factorials. The lecture aims to strengthen students' calculus skills and empower them to tackle a wider array of differentiation problems.
Takeaways
- 📚 Professor Haynes Miller is substituting for David Jerison and will discuss differentiation.
- 📝 Basic differentiation rules include: the derivative of x^n is nx^(n-1), and the derivative of a constant times a function is the constant times the derivative of the function.
- 🔍 The product rule for differentiation states that the derivative of a product of two functions is u'v + uv'.
- 🤔 An example of applying the product rule is differentiating x^n times sin(x), which results in nx^(n-1)sin(x) + x^ncos(x).
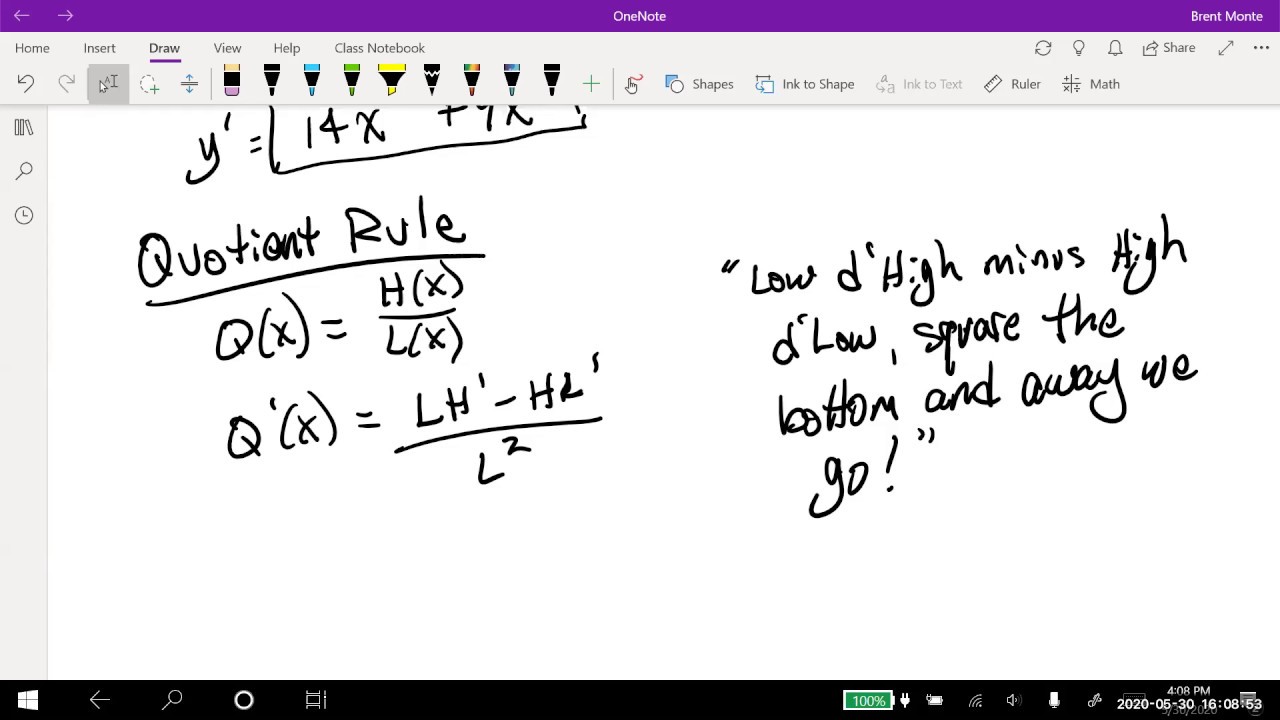
- 🔧 The quotient rule for differentiation states that the derivative of a quotient of two functions is (u'v - uv') / v^2.
- 🔢 The chain rule for differentiation deals with the composition of functions and states that dy/dt = (dy/dx) (dx/dt).
- 📈 An example of the chain rule is differentiating (sin(t))^10, resulting in 10(sin(t))^9cos(t).
- 🔄 Higher derivatives involve differentiating a function multiple times, with notations like u', u'', u''', and u^(n).
- 💡 The nth derivative of x^n results in n! (n factorial), and the (n+1)th derivative of x^n is 0.
- 🧩 The lecture covers the product rule, quotient rule, and chain rule, providing foundational tools for more complex differentiation problems.
Q & A
What is the product rule for differentiation?
-The product rule states that the derivative of a product of two functions u and v is given by (u'v + uv') where u' and v' are the derivatives of u and v respectively.
Can you provide an example of how to apply the product rule?
-Sure, if you want to differentiate x^n times sin(x), you would set u = x^n with derivative u' = nx^(n-1) and v = sin(x) with derivative v' = cos(x). Applying the product rule, the derivative is nx^(n-1)sin(x) + x^n cos(x).
What is the quotient rule for differentiation?
-The quotient rule states that the derivative of a quotient of two functions u and v is given by (u'v - uv') / v^2 where u' and v' are the derivatives of u and v respectively.
Can you explain the chain rule for differentiation?
-The chain rule is used for differentiating a composite function. It states that the derivative of a composite function y = (f(g(t))) is given by dy/dt = (dy/dx) * (dx/dt) where dy/dx is the derivative of the outer function with respect to the intermediate variable x, and dx/dt is the derivative of the inner function with respect to the original variable t.
How would you differentiate a function like (sin(t))^10 using the chain rule?
-You would first consider sin(t) as the inner function and the 10th power as the outer function. By the chain rule, the derivative is 10 * (sin(t))^9 * cos(t), which can also be written as 10sin^9(t)cos(t).
What are higher derivatives?
-Higher derivatives refer to the process of differentiating a function multiple times. The first derivative is denoted as u', the second as u'', the third as u''', and so on. Each successive derivative is the derivative of the previous one.
What happens when you differentiate the sine function four times?
-When you differentiate the sine function four times, you get back the sine function itself. That is, after differentiating sine x four times, the result is sin(x), which is a special property of sine and cosine functions.
What is the nth derivative of x^n?
-The nth derivative of x^n results in n! (n factorial) times x to the power of (n - n), which simplifies to n! because x^0 is 1. This is true for positive integer values of n.
What is the result of applying (n + 1)th derivative to x^n?
-Applying (n + 1)th derivative to x^n results in 0 because you would be differentiating a constant (n!) one more time, and the derivative of a constant is zero.
What is the notation D^n used for in the context of derivatives?
-The notation D^n represents the operation of taking the derivative n times. It is an alternative notation to using prime symbols (') to denote each successive derivative of a function.
How does the script demonstrate the use of mathematical induction?
-The script demonstrates mathematical induction by showing the pattern in the derivatives of x^n and then generalizing that the nth derivative of x^n is n!. This pattern is identified and then used to predict the outcome for the (n + 1)th derivative.
Outlines
📚 Introduction to MIT OpenCourseWare and Differentiation Basics
The script begins with an introduction to MIT OpenCourseWare, emphasizing the importance of donations for the continuation of their free educational resources, with a prompt to visit ocw.mit.edu for more information. Professor Haynes Miller substitutes for David Jerison and reviews basic differentiation concepts, including the derivative of x^n and the sine function. He also covers the rules for differentiating when a function is multiplied by a constant or when differentiating a sum of functions. The main focus for the lecture is announced to be the product rule, quotient rule, composition of functions, and higher derivatives, with an example-driven approach to illustrate these concepts.
🔍 The Product Rule: Differentiation of Functions in Product
The professor introduces the product rule for differentiating a product of two functions, which is formulated as u'v + uv'. He uses the example of differentiating x^n times sin(x) to illustrate the application of the rule. The explanation includes showing the validity of the product rule by examining the change in the product uv as x changes slightly, denoted by delta x. The professor manipulates the expression to involve the changes in u and v separately, leading to the proof of the product rule. The explanation is interactive, with a student asking for clarification on the transition between steps in the derivation.
📈 The Quotient Rule and Its Application
The script moves on to the quotient rule, which is presented as a complex but essential concept for differentiating a quotient of two functions, formulated as (u'v - uv') / v^2. The professor explains the rule with an example and then works through the proof, which involves looking at the change in the quotient when x changes by a small amount, delta x. The cancellation of terms and the final simplification to the quotient rule formula are detailed. An application of the quotient rule is given with the differentiation of 1 / v, and a sub-example with v as a power of x is also provided, showing the resulting formula for the derivative of negative powers of x.
🔗 The Chain Rule: Differentiation of Composite Functions
The chain rule is introduced as a method for differentiating composite functions, such as (sin t)^10. The professor explains the concept of substitution by using a new variable name, x, to represent the intermediate step of the composite function. The chain rule is derived by expressing the change in y with respect to t as a product of the change in y with respect to x and the change in x with respect to t. The rule simplifies to dy/dt = (dy/dx)(dx/dt). An example is given to differentiate (sin t)^10, and the process of substituting back the original variable in place of x is demonstrated.
🔄 Higher Derivatives and Their Computation
The lecture concludes with a discussion on higher derivatives, which are simply the repeated differentiation of a function. The notation for higher derivatives, such as u'' for the second derivative and u''' for the third, is introduced. The professor uses the example of the sine function to illustrate that the fourth derivative of sine results in the sine function itself, highlighting the cyclical nature of the derivatives of trigonometric functions. Different notations for derivatives, such as using d/dx or capital D as an operator, are also explained, with examples of how they can be applied to express higher derivatives.
📝 Mathematical Induction and nth Derivatives of Polynomial Functions
The professor engages in a mathematical induction process to demonstrate the nth derivative of x^n, showing that the result is n factorial (n!) times a constant. This is a specific example that illustrates the pattern of derivatives for polynomial functions. The lecture ends with a question about the (n+1)th derivative of x^n, which the professor answers as zero, since it would be the derivative of a constant. The use of mathematical induction and the concept of factorials are key points in this segment of the lecture.
Mindmap
Keywords
💡Differentiation
💡Product Rule
💡Quotient Rule
💡Chain Rule
💡Higher Derivatives
💡Derivative
💡Continuity
💡Trigonometric Functions
💡Composite Functions
💡Operator
💡Factorial
Highlights
Introduction of the product rule for differentiating a product of functions, expressed as u'v + uv'.
Illustration of the product rule using the example of differentiating x^n * sin(x).
Explanation of the proof behind the product rule involving the change in the product uv when x changes.
Introduction of the quotient rule for differentiating a quotient of functions, expressed as (u'v - uv') / v^2.
Demonstration of the quotient rule with the example of differentiating 1 / v.
Application of the quotient rule to find the derivative of 1 / x^n, resulting in -n - 1.
Introduction of the chain rule for differentiating a composition of functions.
Derivation of the chain rule through the concept of intermediate variables and change in y with respect to t.
Example of applying the chain rule to differentiate (sin t)^10, resulting in sin^9(t)cos(t).
Differentiation of sin(10t) using the chain rule, yielding 10cos(10t).
Discussion on higher derivatives, defined as differentiating a function repeatedly.
Explanation of the notation for higher derivatives, including u'', u''', and u^(n).
Example showing that differentiating the sine function four times results in the original function.
Introduction of alternative notations for derivatives, such as d/dx and D^n.
Calculation of the nth derivative of x^n using the capital D notation, resulting in n!.
Final question and answer about the result of D^(n + 1) applied to x^n, which is 0.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: