Derivatives of Composite Functions - Chain Rule, Product & Quotient Rule

The Organic Chemistry Tutor

9 Sept 201661:02

EducationalLearning

32 Likes 10 Comments

TLDRThis comprehensive video tutorial delves into the intricacies of differentiation, specifically focusing on the Product Rule, Quotient Rule, and Chain Rule as they apply to composite functions. The presenter breaks down each rule methodically, starting with the Product Rule, which is used for finding the derivative of two functions multiplied together. The Quotient Rule is then explored for instances where one function is divided by another, followed by the Chain Rule, which is pivotal for differentiating composite functions. The video is replete with examples that illustrate the application of these rules, providing a clear understanding of how to differentiate complex functions. The presenter also demonstrates how to use data tables to evaluate derivatives at specific points, making the content highly applicable for students and learners in calculus.

Takeaways

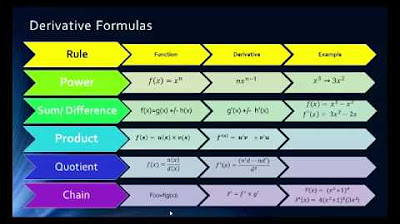
📚 Start with the basics: The video introduces the product rule, quotient rule, and chain rule for derivatives, which are fundamental in calculus for dealing with composite functions.
🤝 Product Rule: To find the derivative of a product of two functions, use the formula f'(x)g(x) + g'(x)f(x), where f(x) and g(x) are the functions being multiplied.
🔄 Quotient Rule: When differentiating a quotient of two functions, apply the formula [g(x)f'(x) - f(x)g'(x)] / [g(x)]^2 to handle the division.
🔗 Chain Rule: For composite functions, such as f(g(x)), the chain rule states that the derivative is f'(g(x)) * g'(x), which means you differentiate the outer function at the inner function's result and multiply by the derivative of the inner function.
📈 Example Application: The video provides examples of how to apply these rules to specific functions, such as x^2 * e^x and x^4 * sin(x), demonstrating the step-by-step process.
🔢 Data Table Utilization: The script explains how to use a data table to evaluate functions and their derivatives, particularly useful for plug-and-chug problems.
📌 Simplification Tips: It's important to simplify expressions after applying the rules, often by factoring out common terms or using algebraic identities.
🧮 FOIL Method: When expanding expressions, the script mentions the FOIL (First, Outer, Inner, Last) method for binomials but advises caution to avoid losing track of terms.
📉 Negative Exponents: The video touches on handling negative exponents by flipping them and adjusting the base, which is a common technique in calculus.
🔁 Repeated Applications: For nested functions like f(f(x)), the process involves applying the derivative rules successively, as demonstrated in the script.
📋 Practice Makes Perfect: The video concludes with a reminder that practice is key to mastering these concepts, encouraging viewers to work through the examples provided.

Q & A

What is the product rule for differentiation?
-The product rule states that the derivative of two functions multiplied together, f(x) * g(x), is given by f'(x) * g(x) + f(x) * g'(x), where f'(x) is the derivative of the first function and g'(x) is the derivative of the second function.
How do you use the product rule to find the derivative of x^2 * e^x?
-Using the product rule, the derivative of x^2 * e^x is (2x) * e^x + (x^2) * e^x, since the derivative of x^2 is 2x and the derivative of e^x is e^x.
What is the quotient rule for differentiation?
-The quotient rule is used to find the derivative of a function that is one function divided by another. It states that the derivative of f(x) / g(x) is [g(x) * f'(x) - f(x) * g'(x)] / [g(x)]^2.
How do you find the derivative of a composite function?
-The derivative of a composite function is found using the chain rule, which states that the derivative of f(g(x)) is f'(g(x)) * g'(x), where f'(g(x)) is the derivative of the outer function evaluated at the inner function, and g'(x) is the derivative of the inner function.
What is the derivative of y = (3x^5 + 7) * (x^3 - 5x) using the product rule?
-The derivative of y = (3x^5 + 7) * (x^3 - 5x) is found by applying the product rule: (15x^4 * (x^3 - 5x)) + (3x^5 + 7) * (3x^2 - 5).
How do you apply the product rule to a function with three parts, like y = x^2 * (5x^3 + 8) * (7x - x^2)?
-You differentiate the first part and keep the other two the same, then differentiate the second part and keep the third the same, and finally differentiate the third part while keeping the first two the same. Combine these results to get the derivative of the three-part function.
What is the derivative of a rational function y = (3x - 1) / (2x + 1)?
-The derivative of the rational function y = (3x - 1) / (2x + 1) is found using the quotient rule and is equal to [(2x + 1) * 3 - (3x - 1) * 2] / (2x + 1)^2.
What is the derivative of y = (x^2) / (x + 5) using the quotient rule?
-The derivative of y = (x^2) / (x + 5) using the quotient rule is [(x + 5) * 2x - x^2 * 1] / (x + 5)^2, which simplifies to (5 - x) / (2 * sqrt(x) * (x + 5)^2).
How do you find the derivative of y = sqrt(x) / (x + 5) using the quotient rule?
-The derivative of y = sqrt(x) / (x + 5) is found by applying the quotient rule: [((x + 5) * 1/(2 * sqrt(x))) - (sqrt(x) * 1)] / (x + 5)^2, which simplifies to (5 - x) / (2 * sqrt(x) * (x + 5)^2).
What is the derivative of the composite function y = (x^3 - 5x)^4?
-The derivative of the composite function y = (x^3 - 5x)^4 is found using the chain rule: 4 * (x^3 - 5x)^3 * (3x^2 - 5).
How do you find the derivative of y = (5x^2 - 7x + 3)^3 using the chain rule?
-The derivative of y = (5x^2 - 7x + 3)^3 is found by applying the chain rule: 3 * (5x^2 - 7x + 3)^2 * (10x - 7).
What is the derivative of y = sin(x^2) using the chain rule?
-The derivative of y = sin(x^2) is found using the chain rule: cos(x^2) * 2x, since the derivative of x^2 is 2x and the derivative of sin(u) is cos(u) with respect to u.
How do you find the derivative of y = tan^3(5x^2 + 8) using the chain rule?
-The derivative of y = tan^3(5x^2 + 8) is found by applying the chain rule: 3 * tan^2(5x^2 + 8) * sec^2(5x^2 + 8) * (10x).
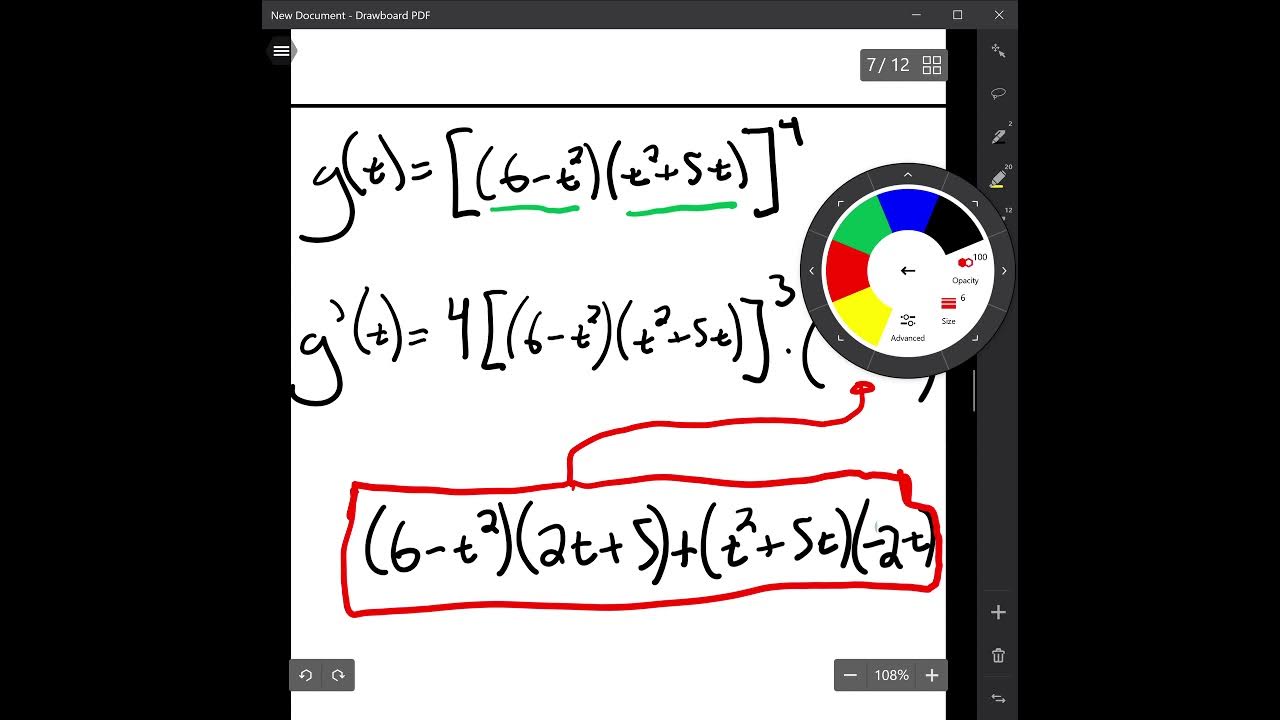
What is the derivative of y = (5 + 4x)^4 * (7x - x^2)^5 using the product rule and chain rule?
-The derivative of y = (5 + 4x)^4 * (7x - x^2)^5 involves applying both the product rule and the chain rule. The derivative, denoted as y', is a complex expression involving terms such as 16(5 + 4x)^3, (7x - x^2)^4, and (7 - 2x), multiplied by the respective derivatives of the inner functions.

Outlines

00:00

📚 Introduction to Derivative Rules

This paragraph introduces the main focus of the video, which is to explain three key differentiation rules: the product rule, the quotient rule, and the chain rule. It sets the stage for a detailed discussion on how to find the derivatives of composite functions.

05:01

🔍 The Product Rule

The video begins with the product rule, explaining how to find the derivative of two functions multiplied together. It provides a formula and walks through examples, such as the function x^2 * e^x, and another with x^4 * sin(x), demonstrating how to apply the rule and simplify the results.

10:01

🔢 Applying the Product Rule to More Complex Functions

The script discusses extending the product rule to functions with three parts, showing how to differentiate y = x^2 + 3x * (5x^3 + 8) * (7x - x^2). It emphasizes the importance of differentiating each part while keeping the others constant and provides a clear example to illustrate the process.

15:02

📉 The Quotient Rule

The quotient rule is introduced for differentiating a function that is the quotient of two other functions. The formula is presented, and the video applies it to the example y = (3x - 1) / (2x + 1), showing each step in detail, including simplifying the expression.

20:05

🛠️ Deriving the Quotient Rule

The video demonstrates how to derive the quotient rule formula by differentiating y = f(u) with respect to x, where u = g(x). It shows the process of substituting u with g(x) and simplifying to obtain the final formula for the quotient rule.

25:05

🏗️ The Chain Rule

The chain rule is introduced for differentiating composite functions. The video explains the concept of a composite function and provides the formula for the chain rule. It then derives the chain rule formula step by step and applies it to the example of differentiating (x^3 - 5x)^4.

30:07

🧮 Differentiating Composite Functions Using Chain Rule

The video shows how to differentiate composite functions using the chain rule by defining y in terms of u and x, and then differentiating with respect to x. It walks through an example where y = u^4 and u = x^3 - 5x, and demonstrates how to find dy/dx.

35:10

🔗 Simplifying the Chain Rule Process

The video simplifies the process of using the chain rule by directly applying the formula to differentiate composite functions. It provides an example with y = (5x^2 - 7x + 3)^3 and shows the simplified method to find the derivative dy/dx.

40:11

🌀 Applying the Chain Rule to Trigonometric Functions

The script discusses the application of the chain rule to trigonometric functions, such as y = sin(x^2) and y = tan^3(5x^2 + 8), showing how to differentiate these functions step by step, moving from the outside to the inside of the function.

45:23

🧩 Combining Product and Chain Rules

The video tackles a complex problem that combines the product and chain rules. It shows how to find the derivative of an expression like y = (5 + 4x)^4 * (7x - x^2)^5, factoring out common terms and simplifying the expression to find y'.

50:25

📊 Using a Data Table for Derivatives

The video concludes with examples of using a data table to find derivatives for functions defined as the product or quotient of two other functions, or as composite functions. It demonstrates how to calculate h'(2), h'(1), and h'(0) using given values from the table.

55:26

📈 Evaluating Composite Functions with Data Tables

The final part of the script shows how to evaluate the derivative of composite functions using a data table. It provides examples for calculating h'(2), h'(1), and h'(0) when the function h(x) is defined as a composition of other functions, using the values from the table to find the derivative.

00:27

🎓 Conclusion

The video wraps up with a summary of how to solve problems involving product, quotient, and chain rules, as well as using data tables for derivatives. It thanks the viewers for watching and encourages them to practice these techniques.

Mindmap

Keywords

💡Product Rule

The Product Rule is a fundamental principle in calculus for differentiating products of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function, plus the first function times the derivative of the second function. In the video, this rule is applied to functions like x^2 * e^x, demonstrating how to find their derivatives using the Product Rule.

💡Quotient Rule

The Quotient Rule is used to find the derivative of a quotient of two functions. It is expressed as the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. The video illustrates the Quotient Rule's application with an example involving the function (3x - 1) / (2x + 1), showing each step to find its derivative.

💡Chain Rule

The Chain Rule is essential for differentiating composite functions, which are functions composed of one function inside another. It states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. The video script provides several examples to demonstrate the use of the Chain Rule, such as differentiating (x^3 - 5x)^4.

💡Derivative

A derivative in calculus represents the rate of change of a function with respect to its variable. It is a key concept in the study of functions and their behavior. The video focuses on finding derivatives using various rules such as the Product Rule, Quotient Rule, and Chain Rule, which are all methods to compute derivatives of different types of functions.

💡Composite Function

A composite function is a function formed by applying one function to the result of another. It is typically denoted as f(g(x)). The video explains how to find the derivatives of composite functions using the Chain Rule, which is crucial for more complex functions that are not simple polynomials or exponentials.

💡Power Rule

The Power Rule is a basic rule in calculus that allows the differentiation of power functions, which are of the form f(x) = x^n, where n is a constant. The rule states that the derivative of x^n is n*x^(n-1). The video uses the Power Rule in multiple examples, such as when differentiating x^4 or (x^3 - 5x)^4.

💡Sine Function

The sine function is a trigonometric function that represents the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle. In the video, the sine function is used in examples to demonstrate how its derivative, which is the cosine function, can be found using the Chain Rule.

💡Cosine Function

The cosine function, like the sine function, is a trigonometric function that describes specific ratios in right-angled triangles. The video mentions the cosine function in the context of derivatives, showing that the derivative of sine is cosine, and vice versa, which is a fundamental concept in calculus.

💡Tangent Function

The tangent function, another trigonometric function, is the ratio of the sine to the cosine of an angle. The video script includes an example where the derivative of a function involving the tangent function is found using the Chain Rule, emphasizing the tangent function's role in calculus when dealing with trigonometric expressions.

💡Secant Function

The secant function is the reciprocal of the cosine function, which means it is the ratio of 1 to the cosine of an angle. The video briefly touches on the secant function when discussing derivatives of trigonometric functions, noting that its derivative is secant times the tangent of the angle.

💡Data Table

A data table is a structured representation of data in rows and columns, often used to organize and display specific values for different variables. In the video, a data table is used to provide values for functions and their derivatives at certain points, allowing for the application of rules like the Product Rule, Quotient Rule, and Chain Rule to find derivative values at specific x-values.

Highlights

The video covers the Product Rule, Quotient Rule, and Chain Rule for derivatives of composite functions.

The Product Rule is introduced for finding the derivative of two functions multiplied together.

The Quotient Rule formula is explained for differentiating a function divided by another function.

The Chain Rule is detailed for composite functions, where one function is within another.

An example demonstrates using the Product Rule for a function involving x squared and e to the power of x.

The Quotient Rule is applied to a rational function of (3x - 1) / (2x + 1).

The Chain Rule is used to find the derivative of a composite function like x cubed minus 5x raised to the fourth power.

The video explains how to derive the formula for the Chain Rule using dy/du and du/dx.

An alternative method for finding derivatives using dy/du and du/dx is demonstrated with an example.

The video shows how to use the Chain Rule for more complex composite functions, like the fourth root of x squared plus 2x minus 9.

The application of the Product Rule and Chain Rule together is exemplified in a problem involving multiple functions.

The video demonstrates how to use a data table to calculate derivatives using the Product and Quotient Rules.

Calculating h'(2) using the Product Rule with a given data table is shown step by step.

The Quotient Rule is used to calculate h'(1) with the help of a data table.

The Chain Rule is applied to evaluate h'(0) for a composite function f(g(x)) using a data table.

The video concludes with a complex composite function example, h(x) = g(g(x)), and calculates h'(1).

Practical examples and step-by-step solutions are provided to illustrate the application of derivative rules.

Transcripts

Browse More Related Video

Derivatives of Composite Functions: The Chain Rule

1.7 - The Chain Rule

Math 1325 Lecture 9 7 - Using Derivative Forumulas

Derivatives with Multiple Rules

The Chain Rule - Part 2

The Chain Rule

Related Tags

Calculus Product Rule Quotient Rule Chain Rule Derivatives Composite Functions Mathematics Educational Content Math Tutorial Function Analysis Rule Application