Lesson 4 - Inverse Hyperbolic Functions (Calculus 2 Tutor)

Math and Science
18 Aug 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThis Advanced Calculus 2 tutorial continues the exploration of hyperbolic functions, specifically focusing on inverse hyperbolic functions and their derivatives. The instructor draws parallels to previously discussed inverse trigonometric functions, emphasizing the concept of inverse functions as opposites that can revert to the original input when applied sequentially. The video provides the derivative formulas for inverse hyperbolic sine, cosine, tangent, and cotangent without derivation, intending to equip viewers with the tools to solve related calculus problems. The derivatives are presented as follows: inverse hyperbolic sine (1/√(1+x^2)), inverse hyperbolic cosine (1/√(x^2-1)), inverse hyperbolic tangent (1/(1-x^2)), and inverse hyperbolic cotangent (1/(1-x^2)), highlighting the similarity between the derivatives of the tangent and cotangent functions.

Takeaways
  • 📚 The tutorial continues from the previous session on hyperbolic functions and their derivatives.
  • 🔍 The focus of the session is on inverse hyperbolic functions and their derivatives, following a similar pattern to the earlier discussion on inverse trigonometric functions.
  • 🔑 The inverse hyperbolic functions are the opposites of their corresponding hyperbolic functions, similar to how inverse trigonometric functions work.
  • 👉 For example, the inverse of the hyperbolic sine function is denoted as 'hyperbolic inverse of X'.
  • 🧠 The concept of inverse functions is reviewed, emphasizing the relationship between a function and its inverse, where input and output are reversed.
  • 📉 The derivatives of the inverse hyperbolic functions are provided without derivation, to be used for solving problems.
  • ✏️ The derivative of the inverse hyperbolic sine is given as '1 over the square root of (1 + x squared)'.
  • 📐 The derivative of the inverse hyperbolic cosine is '1 over the square root of (x squared - 1)'.
  • 📈 The derivative of the inverse hyperbolic tangent is '1 over (1 - x squared)', which is identical to the derivative of the inverse hyperbolic cotangent.
  • 🔄 There is a noticeable similarity in the form of the derivatives of inverse hyperbolic functions, with adjustments based on the specific function.
  • 📝 The session aims to equip students with the knowledge of how to take derivatives of inverse hyperbolic functions for use in tests and problem-solving.
Q & A

  • What topic is being discussed in the video script?

    -The video script discusses the topic of inverse hyperbolic functions and their derivatives.

  • What was the focus of the previous section in the course?

    -The previous section focused on hyperbolic functions and their derivatives.

  • What is the relationship between a hyperbolic function and its inverse?

    -The relationship is that the inverse hyperbolic function reverses the operation of the original hyperbolic function, allowing you to retrieve the original input when applied to the output of the original function.

  • How is the notation for the inverse of a hyperbolic function represented?

    -The notation for the inverse of a hyperbolic function is represented with a negative sign (-) in front of the function name, which indicates the inverse function.

  • What is the derivative of the inverse hyperbolic sine function with respect to x?

    -The derivative of the inverse hyperbolic sine function with respect to x is 1 over the square root of (1 + x squared).

  • What is the derivative of the inverse hyperbolic cosine function with respect to x?

    -The derivative of the inverse hyperbolic cosine function with respect to x is 1 over the square root of (x squared - 1).

  • How does the derivative of the inverse hyperbolic tangent function compare to the derivative of the inverse hyperbolic cotangent function?

    -The derivative of the inverse hyperbolic tangent function is exactly the same as the derivative of the inverse hyperbolic cotangent function, which is 1 over (1 - x squared).

  • What is the significance of the inverse hyperbolic functions in relation to inverse trigonometric functions?

    -The significance is that inverse hyperbolic functions are exact analogues of inverse trigonometric functions, following the same principles of reversing the operation of the original function to retrieve the original input.

  • What is the main purpose of discussing the derivatives of inverse hyperbolic functions in the script?

    -The main purpose is to provide students with the formulas for the derivatives of inverse hyperbolic functions so they can solve problems involving these functions.

  • Why is it important to understand the concept of inverse functions in the context of calculus?

    -Understanding inverse functions is important because it helps in solving equations and problems where the original function is not easily invertible, and it is a fundamental concept in calculus that extends to various mathematical applications.

Outlines
00:00
📚 Introduction to Inverse Hyperbolic Functions

This paragraph introduces the topic of inverse hyperbolic functions, continuing from the previous section on hyperbolic functions and their derivatives. The instructor emphasizes the similarity between inverse hyperbolic functions and the previously discussed inverse trigonometric functions. The concept of inverse functions is briefly reviewed, highlighting how they are opposites that can reverse the output of the original function back to its original input. The paragraph sets the stage for the upcoming discussion on the derivatives of inverse hyperbolic functions without delving into proofs or derivations.

Mindmap
Keywords
💡Advanced Calculus 2
Advanced Calculus 2 is a higher-level course in calculus that typically follows the study of Calculus 1 and focuses on more complex concepts and techniques. In the context of the video, this course is the setting for the discussion of hyperbolic functions and their derivatives, indicating that the content is aimed at students who have a solid foundation in calculus and are ready to explore more advanced topics.
💡Hyperbolic Functions
Hyperbolic functions are a set of mathematical functions that are analogs of the trigonometric functions but are defined in terms of exponential functions. They include functions like hyperbolic sine (sinh), hyperbolic cosine (cosh), and hyperbolic tangent (tanh), among others. In the video, the tutor is building on the previous discussion of these functions and their derivatives, showing their importance in the study of advanced calculus.
💡Inverse Hyperbolic Functions
Inverse hyperbolic functions are the inverse operations of the hyperbolic functions, similar to how inverse trigonometric functions are the inverses of sine, cosine, and tangent. They include inverse hyperbolic sine (sinh^-1), inverse hyperbolic cosine (cosh^-1), and inverse hyperbolic tangent (tanh^-1). The video script discusses these functions and their derivatives, which are essential for solving calculus problems involving inverse hyperbolic functions.
💡Derivatives
Derivatives in calculus represent the rate at which a function changes with respect to its variable. They are fundamental to understanding the behavior of functions and are a key concept in the study of calculus. In the video, the tutor discusses the derivatives of inverse hyperbolic functions, which are crucial for students to master in order to solve related calculus problems.
💡Inverse Functions
Inverse functions are functions that 'reverse' the effect of the original function, returning the input value when given the output value. For example, if a function f(x) = y, then its inverse function f^-1(y) would return x. In the video, the concept of inverse functions is applied to hyperbolic functions, and the tutor explains how to find and use the inverse hyperbolic functions.
💡Trigonometric Functions
Trigonometric functions are a set of functions that relate the angles of a triangle to the lengths of its sides. They include sine, cosine, and tangent, among others. The video script mentions these functions as a way to draw parallels between the properties of inverse trigonometric functions and inverse hyperbolic functions, highlighting the similarities in their inverse operations.
💡Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the symbol √. In the context of the video, square roots appear in the formulas for the derivatives of inverse hyperbolic functions, indicating that they play a role in the calculation of these derivatives.
💡Exponential Functions
Exponential functions are mathematical functions of the form f(x) = a * b^x, where a and b are constants, and b > 0. They are the foundation of hyperbolic functions, as hyperbolic functions are defined in terms of exponential functions. The video script does not explicitly mention exponential functions, but understanding them is crucial for grasping the concept of hyperbolic functions.
💡Inverse Trigonometric Functions
Inverse trigonometric functions are the inverses of the basic trigonometric functions and are used to find the angle when the ratio of the sides of a right triangle is known. They include arcsine (sin^-1), arccosine (cos^-1), and arctangent (tan^-1). The video script uses these functions as an analogy to explain the concept of inverse hyperbolic functions, showing the students how they are similar in their inverse nature.
💡Test
In the context of the video, 'test' refers to an examination or assessment that students might take to demonstrate their understanding of the course material. The tutor mentions that the students should remember the derivatives of inverse hyperbolic functions for their tests, emphasizing the practical application of these concepts in an academic setting.
Highlights

Introduction to inverse hyperbolic functions and their derivatives as a continuation of the previous section on hyperbolic functions.

Pattern of discussing inverse functions and their derivatives, previously seen with inverse trigonometric functions.

Inverse hyperbolic sine function denoted as hyperbolic sine of inverse X.

Inverse hyperbolic cosine function denoted as hyperbolic cosine of inverse X.

Explanation of the notation for inverse functions, emphasizing it is not an exponent but a symbol for inverse.

Concept of inverse functions where input and output are reversed, analogous to inverse trigonometric functions.

Motivation for inverse hyperbolic functions as exact analogues to inverse trigonometric functions.

Derivative of the inverse hyperbolic sine is 1 over the square root of (1 + x squared).

Derivative of the inverse hyperbolic cosine is 1 over the square root of (x squared - 1).

Derivative of the inverse hyperbolic tangent is 1 over (1 - x squared).

Derivative of the inverse hyperbolic cotangent is the same as the inverse hyperbolic tangent, 1 over (1 - x squared).

Similarity between the derivatives of inverse hyperbolic tangent and cotangent.

No proof or derivation of the derivatives, only their presentation for practical use.

Use of these derivatives to solve problems in advanced calculus.

Emphasis on memorizing the derivatives for application in tests and problem-solving.

The transcript ends with a note on the derivative of inverse hyperbolic functions.

Transcripts

Browse More Related Video

Derivative of Inverse Trig Functions via Implicit Differentiation

Derivatives of Inverse Functions

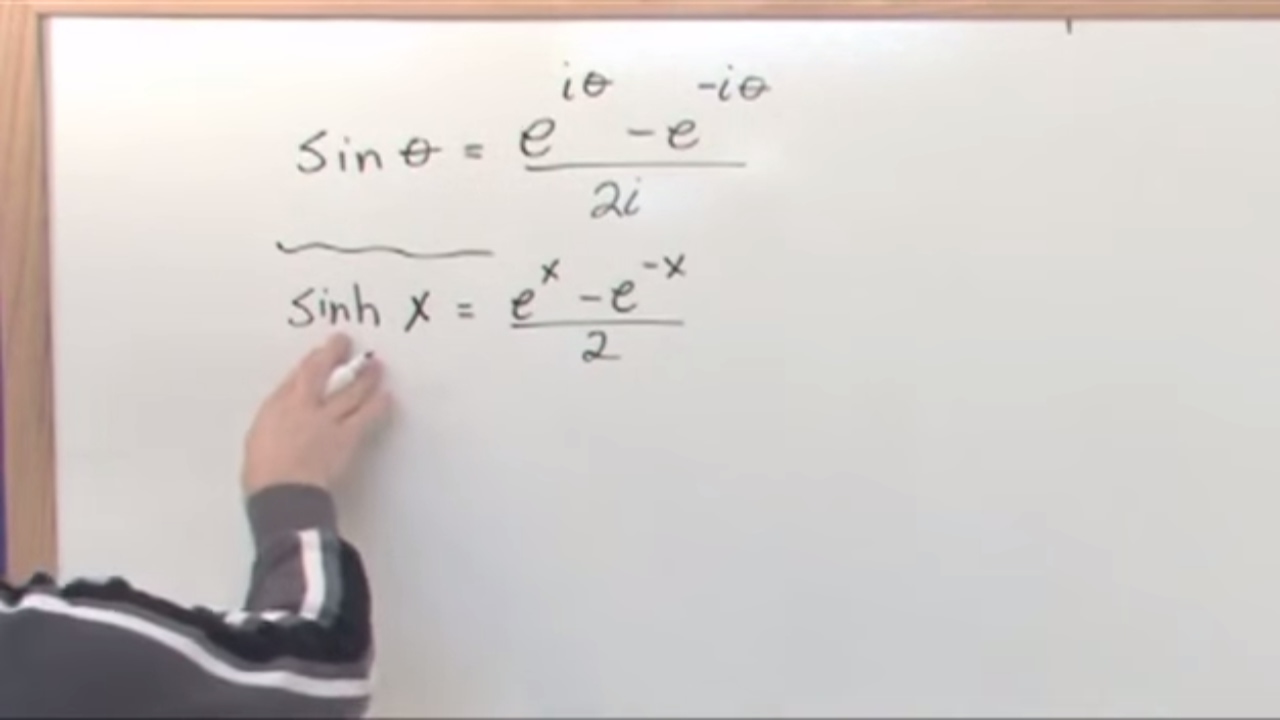
Lesson 3 - Hyperbolic Functions (Calculus 2 Tutor)

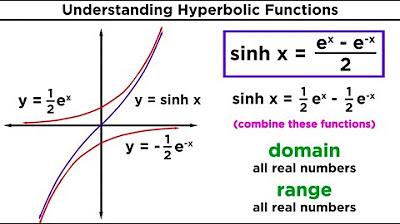
Hyperbolic Functions: Definitions, Identities, Derivatives, and Inverses

Derivative of inverse cosine | Taking derivatives | Differential Calculus | Khan Academy

DERIVATIVES that keep getting HARDER 🤯 | jensenmath.ca

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Advanced CalculusHyperbolic FunctionsInverse FunctionsDerivativesTrigonometryEducational ContentMathematics TutorialInverse TrigonometricCalculus 2Function Derivatives