Calculating the Gravitational Force
TLDRIn this AP Physics essentials video, Mr. Andersen explains the concept of gravitational force and why we feel weightless in space despite gravity's presence. He illustrates this with the analogy of a cannonball launched at varying speeds, showing that at a certain velocity, it will orbit the Earth, creating a weightless sensation. The video delves into Newton's Law of Universal Gravitation, providing the formula to calculate gravitational force between two masses. Andersen uses an example to demonstrate the calculation and challenges viewers to calculate the gravitational force acting on a person standing on the Moon's surface, emphasizing that gravity does not disappear when orbiting Earth.
Takeaways
- 🌍 Gravity is a force that holds us to the planet, and it is also responsible for the orbits of the moon around the Earth and the Earth around the Sun.
- 🚀 Weightlessness in space is not due to the absence of gravity but because the gravitational force is balanced by the centripetal force required for orbiting.
- 🎯 Newton's Law of Universal Gravitation explains and quantifies the gravitational force between two masses.
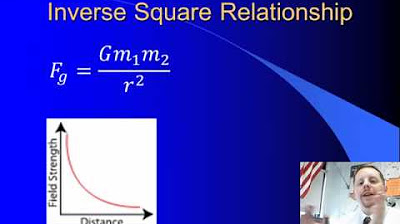
- 🔢 The gravitational force equation is F = G * (m1 * m2) / r^2, where F is the force, G is the gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the masses.
- 📚 The gravitational constant (G) is approximately 6.67 × 10^-11, a value worth memorizing.
- 🌐 The gravitational force is always attractive and acts between any two masses, regardless of their size.
- 📈 The force of gravity increases with the mass of the objects and decreases with the square of the distance between them.
- 📊 The gravitational force is directly proportional to the product of the masses and inversely proportional to the square of the distance between their centers.
- 🌕 On Earth, the gravitational acceleration (g) is essentially constant due to the large mass and size of the Earth compared to the small changes in distance from its center.
- 📚 A simple problem in physics class might involve calculating the gravitational force between two objects using the given equation and known values for mass and distance.
- 🌘 The gravitational force on the surface of the Moon would be weaker than on Earth due to the Moon's smaller mass and the distance from its center to the surface.
Q & A
What is the force of gravity and why do we not experience it in space?
-The force of gravity is the attractive force that holds us to the planet. In space, especially when orbiting a planet like Earth, we do not feel this force because we are in a state of continuous free fall towards the Earth, but we keep missing it, which results in a sensation of weightlessness.
How did Newton explain the concept of weightlessness in space?
-Newton explained that if an object is launched at a high enough speed, it will keep falling towards the Earth but will also keep missing it, resulting in an orbit around the Earth. Inside such an object, like a satellite, one would feel weightless due to the continuous free fall.
What is the formula for calculating the gravitational force between two objects?
-The formula for calculating the gravitational force (F) between two objects is F = G * (m1 * m2) / r^2, where G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between the centers of the two objects.
What is the value of the gravitational constant (G)?
-The gravitational constant (G) is approximately 6.67 × 10^-11 N(m/kg)^2.
Why does the gravitational force increase when the masses of the objects are increased?
-The gravitational force increases with the product of the masses of the two objects (m1 * m2). Therefore, if the mass of either object is increased, the overall gravitational force between them also increases.
How does the distance between two objects affect the gravitational force?
-The gravitational force is inversely proportional to the square of the distance (r^2) between the centers of the two objects. This means that if the distance is doubled, the force is reduced to a quarter of its original value.
What is the significance of the term 'center-center distance' in the gravitational force formula?
-The 'center-center distance' refers to the distance between the centers of mass of the two objects. It is important because the gravitational force depends on the distance between the two objects, not their surface-to-surface distance.
Why is the gravitational acceleration (g) considered constant on Earth?
-The gravitational acceleration (g) is considered constant on Earth because the Earth's mass is so large compared to our own, and the changes in our distance from the Earth's center are relatively small, so the gravitational force does not vary significantly over the surface of the Earth.
Can you provide an example of how to calculate the gravitational force between two objects?
-Sure, if you have two 3.0 kg masses that are 2.0 meters apart, the gravitational force between them can be calculated using the formula F = G * (m1 * m2) / r^2. Plugging in the values, you get F = (6.67 × 10^-11 N(m/kg)^2) * (3 kg * 3 kg) / (2 m)^2, which simplifies to 1.5 × 10^-10 N.
What is the gravitational force acting on a person standing on the surface of the Moon?
-To calculate the gravitational force acting on a person on the Moon's surface, you would use the same formula F = G * (m1 * m2) / r^2, but you would need to know the mass of the Moon, the mass of the person, and the distance from the Moon's center to the surface where the person is standing.
How does Newton's second law of motion relate to the gravitational force?
-According to Newton's second law of motion, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F = ma). By dividing the gravitational force by the mass of an object, you can find the acceleration due to gravity, which on the Moon is about a sixth of what it is on Earth.
Outlines
🚀 Understanding Gravitational Force and Weightlessness
In this segment, Mr. Andersen introduces the concept of gravitational force and how it affects objects in space. He explains that gravity does not cease to exist in space, contrary to common misconceptions. Instead, he uses the analogy of a cannonball launched at different speeds from a mountaintop to illustrate how gravity influences its trajectory. At a certain speed, the cannonball would orbit the Earth, missing it continuously, which is the principle behind satellite orbits. This is how astronauts experience weightlessness, not due to the absence of gravity, but because they are in continuous free fall around Earth. Newton's Law of Universal Gravitation is highlighted as the key to understanding and quantifying this phenomenon.
📚 Calculating Gravitational Force Using Newton's Law
This paragraph delves into the mathematical aspect of Newton's Law of Universal Gravitation. Mr. Andersen provides the formula for calculating the gravitational force between two masses, which is an attractive force that depends on the masses involved and the distance between their centers. The formula is presented as F = G * (m1 * m2) / r^2, where G is the gravitational constant (6.67 x 10^-11), m1 and m2 are the masses, and r is the distance between the centers of the two objects. The importance of the distance being squared is emphasized, as it significantly affects the force's magnitude. An example problem is given to demonstrate the calculation of the gravitational force between two 3.0 kg masses separated by 2.0 meters, resulting in a very small force of 1.5 x 10^-10 newtons. Additionally, a challenge is posed to the viewer to calculate the gravitational force acting on Mr. Andersen standing on the moon's surface, hinting at the factors needed to solve such a problem, including the moon's mass, his mass, and the center-center distance from the moon's center to his standing position.
Mindmap
Keywords
💡Gravitational Force
💡Weightlessness
💡Newton's Law of Universal Gravitation
💡Satellites
💡Mass
💡Center-center Distance
💡Gravitational Constant (Big G)
💡Spherically Symmetrical Objects
💡Gravitational Acceleration (G)
💡Newton's Second Law of Motion
Highlights
Introduction to calculating gravitational force in AP Physics essentials video 45.
Explanation of why we don't experience gravity in space, despite its presence.
Newton's explanation of gravity and weightlessness in space.
Satellites' orbiting mechanism explained through gravitational force.
Newton's Law of Universal Gravitation as a tool to understand and quantify gravitational force.
The equation for gravitational force between two masses.
Description of the gravitational constant (big G) and its value.
The concept of spherically symmetrical objects in gravitational force calculations.
How gravitational acceleration (G) remains constant on Earth due to its mass and distance.
Demonstration of gravitational force increase with mass and decrease with distance using a simulation.
Calculation example of gravitational force between two 3.0 kg masses 2.0 meters apart.
Result of the calculation showing an incredibly small gravitational force value.
Assignment of a problem to calculate the gravitational force acting on a person standing on the moon.
Details needed to solve the moon gravity problem: mass of the moon, mass of the person, and center-center distance.
Application of Newton's second law of motion to find acceleration due to gravity on the moon.
The constancy of gravity's effect on Earth's surface due to Earth's mass and size.
Encouragement to learn how to use Newton's law of gravitation to calculate forces between objects.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: